Question

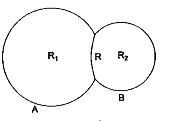
${\displaystyle R_1}$ त्रिज्या के साबुन का एक बुलबुला ${\displaystyle R_2}$ त्रिज्यावाले दूसरे बुलबुले की बाहरी सतह के साथ संपर्क करता है। यदि ${\displaystyle R_1>R_2}$ हो, तो सिद्ध करें कि संपर्की तल की वक्रता-त्रिज्या ${\displaystyle R=\frac{R_1{R}_2}{R_1-R_2}}$.

Explanation

यदि वायुमंडलीय दाब `p_(0)` तथा साबुन के घोल का पृष्ठ-तनाव `gamma` हो, तो `A` तथा `B` के भीतर के दाब क्रमश :
`P_(A)=p_(0)+(4gamma)/(R_(1))` तथा `P_(B)=p_(0)+(4gamma)/(R_(2))`
चूँकि `R_(1) gt R_(2)` , अतः `P_(B) gt P_(A)`.
यदि संपर्की तल की त्रिज्या R हो, तो इसके दोनों ओर के दाबो का अंतर `=(4gamma)/(R )`.
`:.P_(B)-P_(A)=(4gamma)/(R )`
या `(p_(0)+(4gamma)/(R_(2)))-(p_(0)+(4gamma)/(R_(1)))=(4gamma)/(R )`
या `((1)/(R_(2))-(1)/(R_(1)))=(1)/(R )`.
`:.` संपर्की तल की अभीष्ट वक्रता-त्रिज्या `R=(R_(1)R_(2))/(R_(1)-R_(2))` प्रमाणित।