A cubical metal block of edge 12 cm floats in mercry with one fifth of the height inside the mercury. Water poured till the surface of the block is just immersed in it. Find the height of the water column to be poured. Specific gravity of mercury =13.6.Solution in Tamil
The correct Answer is:A, C, D
Given x=12cm
=length of the edge of the block
PHg=13.6gm<br>Given that initially 15 of block is inside mercury.
LetPb→densityofblock∈gm.<br>:(x)^3xxrho_bxxg=(x)^2x(x/5)xxrho_(Hg)xxg<br>rarr (12)^3xxrho_bxxg=(12^2xx12/5xx13.6<br>rho_b=13.6/g gm/cc<br>Afterwaterpured≤tx=heightofwatercolumn.<br>V_b=V_(Hg)+V_w(12)^3<br>WhereV_(Hg)andV_warevolumesofblock∈smercuryandwaterrespectively.<br>:. (V_bxxrho_bxxg)=(V_(Hg)xxrho(Hg)xg)+(V_wxxrho_wxxg)<br>rarr (V_(Hg)xxV_m)xx13.6/5<br>=V_(Hg)xx13.6xxV_wxx1<br>rarr (12)^3xx13.6/5=(12-x)xx13.6+(x)<br>rarr 12.6x=13.6(12-12/5)<br>=(13.6)xx(9.6)<br>rarr x=((9.6)xx(13.6))/(12.6)=10.4cm
Topper's Solved these Questions
Similar Questions
Find the accelerationof the moon with respect to the eath from the following data, Distance between the earth and the moon =3.85×105 km and the time taken by the moon to complete one revolution around the earth =27.3days
View SolutionA body slipping on a rough horizontal plane moves wioth a deceleationof 4.0ms. What is cofficient of kineic friction between the block and the plane?
View SolutionThe liquids shown in figure in the two arms are mercury (specific gravity =13.6) and water. If the difference of heights of the mercury columns is 2 cm, find the height of the water column.
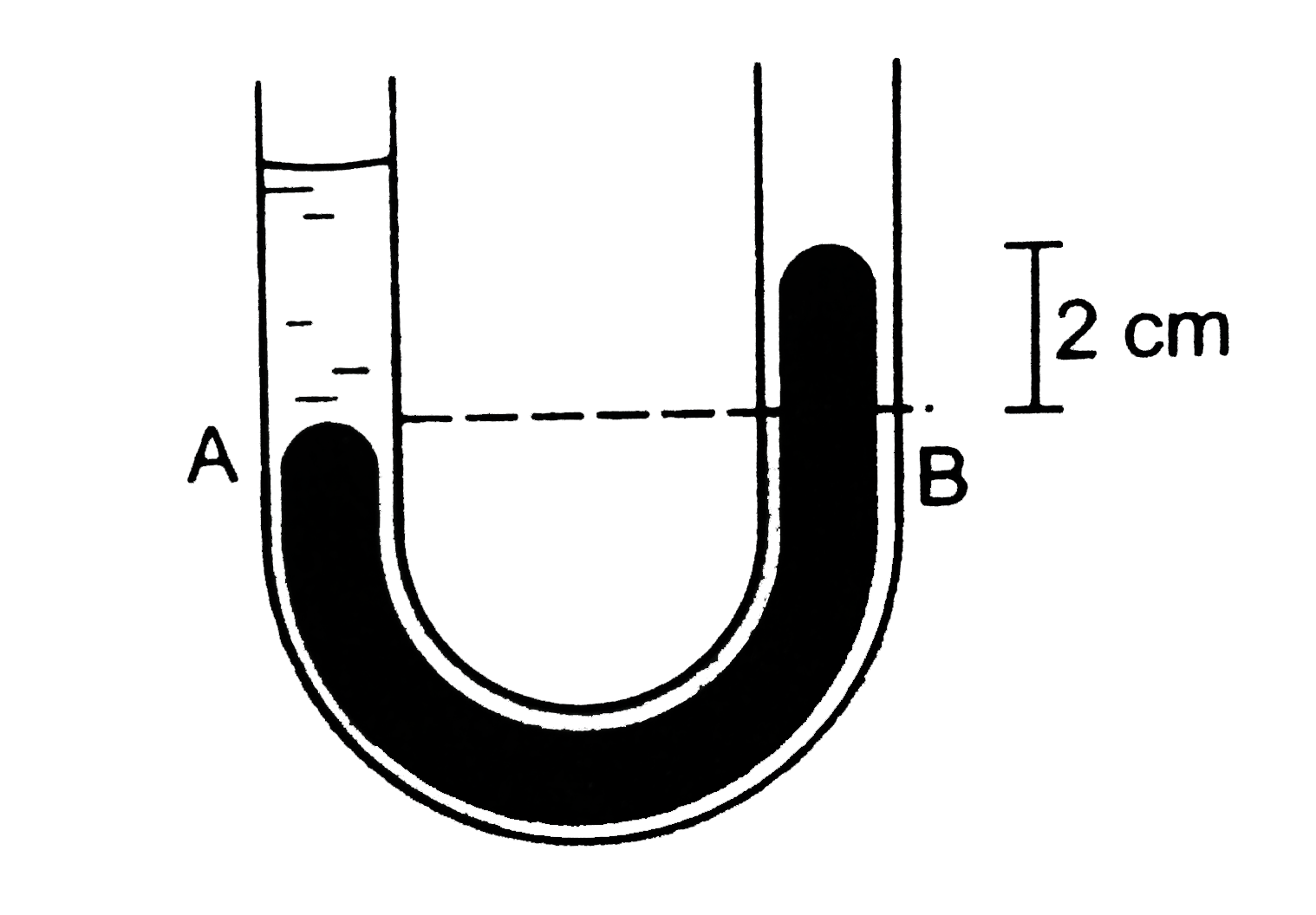 ,
,
View SolutionA cubical metal block of edge 12 cm floats in mercry with one fifth of the height inside the mercury. Water poured till the surface of the block is just immersed in it. Find the height of the block is just immersed in it. Find the height of the water column to be poured. Specific gravity of mercury =13.6.
View SolutionA cube of iron of edge 5 cm floats on the surface of mercury, contained in a tank. Water is then poured on top, so that the cube just gets immersed. Find the depth of water layer. (Specific gravities of iron-and mercury are 7.8 and 13.6 , respectively.)
View SolutionA cubical block of copper of side 10cm is floating in a vessel containing mercury. Water is poured into the vessel so that the copper block just gets submerged. The height of water column is ( rho_(Hg) = 13.6 g//c c , rho_(Cu) = 7.3 g//c c , rho_(water) = 1gm//c c)
View Solution(i) A cubical metal block of side 10cm is floating in a vessel contatining mercury. The vesel has a square cross section of side length 15cm. Water is poured into the vessel so that the metal block just gets submerged. Calculate the mass of water that was poured into the vessel. It is given that relative density of the metal and mercury are 7.3 and 13.6 respectively.
(ii) In the last question, in place of water if we poured another liquid of relative density 'r' it was found that when the metal block ws just completely submerged it was no longer touching mercury. what is value of r?
View SolutionA cubical block of iron 5 cm on each side is floating on mercury in a vessel. (i) what is the height of the block above mercury level ? (ii) Water is poured in the vessel unitl it just covers the iron block. What is the height of water column . density of mercur 13.6 gm//cm^(3) . Density of iron 7.2 gm//cm^(3)
View SolutionA tank contains water on top of mercury as shown in figure. A cubical block of side 10 cm is in equilibrium inside the tank. The depth of the block inside mercury is (RD of the material of block =8.56, RD of mercury =13.6)

View Solutionधातु से बने एक घनाकार ब्लॉक के किनारे की लंबाई 12 cm है और वह अपने 1/5 भाग को डुबोते हुए पारे में तैरता है | ब्लॉक की सतहों को क्षैतिज और ऊर्ध्वाधर स्थिति में रखा जाता है | इस बरतन में इतना पानी डाला जाता है ताकि इस घनाकार ब्लॉक की ऊपरी सतह पानी की सतह पर आ जाए | पारे के ऊपर पानी की ऊँचाई निकालें | पारे का विशिष्ट घनत्व =13.6.
View SolutionA cylindrical vessel is filled with mercury and water of equal weights. The total height of the two liquid layers is 29.2 cm. If the specific gravity of mercury is 13.6, then the height of mercury column will be
View SolutionA body is floating on mercury keeping its 14th part inside mercury. Now, water is poured into the container such that the body remains just immersed totally in water. Now what part of the body will remain immersed in mercury? [Density of mercury = 13.6g⋅cm−3]
View SolutionEach side of an iron cube is 5 cm. This cube floats on mercury. What height of the cube remains above the surface of mercury? To cover the cube, if water is poured over mercury, then what will be the height of the water column? The density of iron is 7.2g⋅cm−3 and the density of mercury is 13.6g⋅cm−3.
View SolutionOne third height of a cubical block of edge 6cm is floating in kerosene oil of specific gravity 0.8. To make the block to be just immersed some water is poured. What is the height of the water column?
View SolutionThe liquids shown in figure in the two arms are mercury (specific gravity =13.6) and water. If the difference of heights of the mercury columns is 2 cm, find the height of the water column.
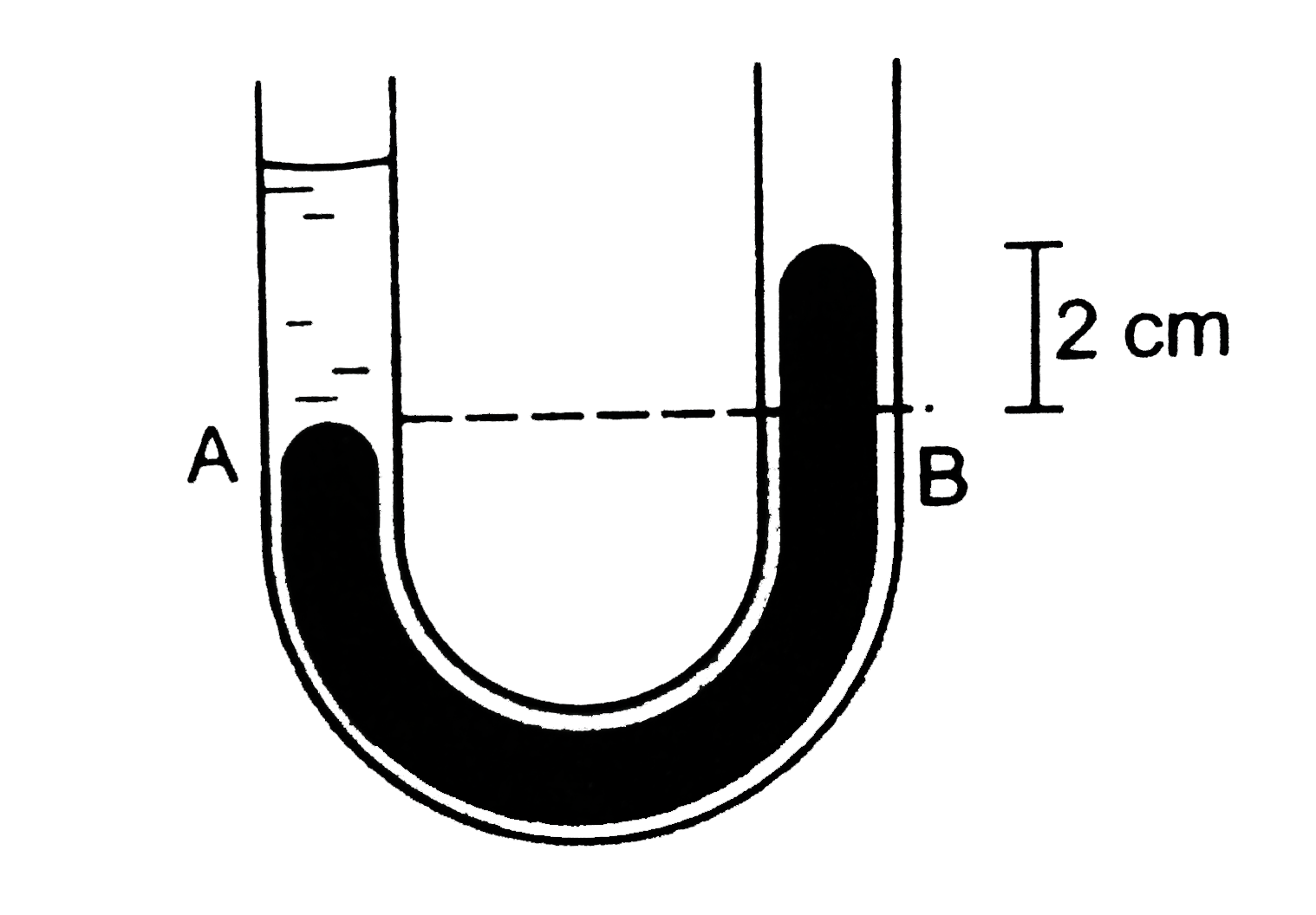 ,
,
View SolutionThe liquids shown in figure in the two arms are mercury (specific gravity =13.6) and water. If the difference of heights of the mercury columns is 2 cm, find the height of the water column.
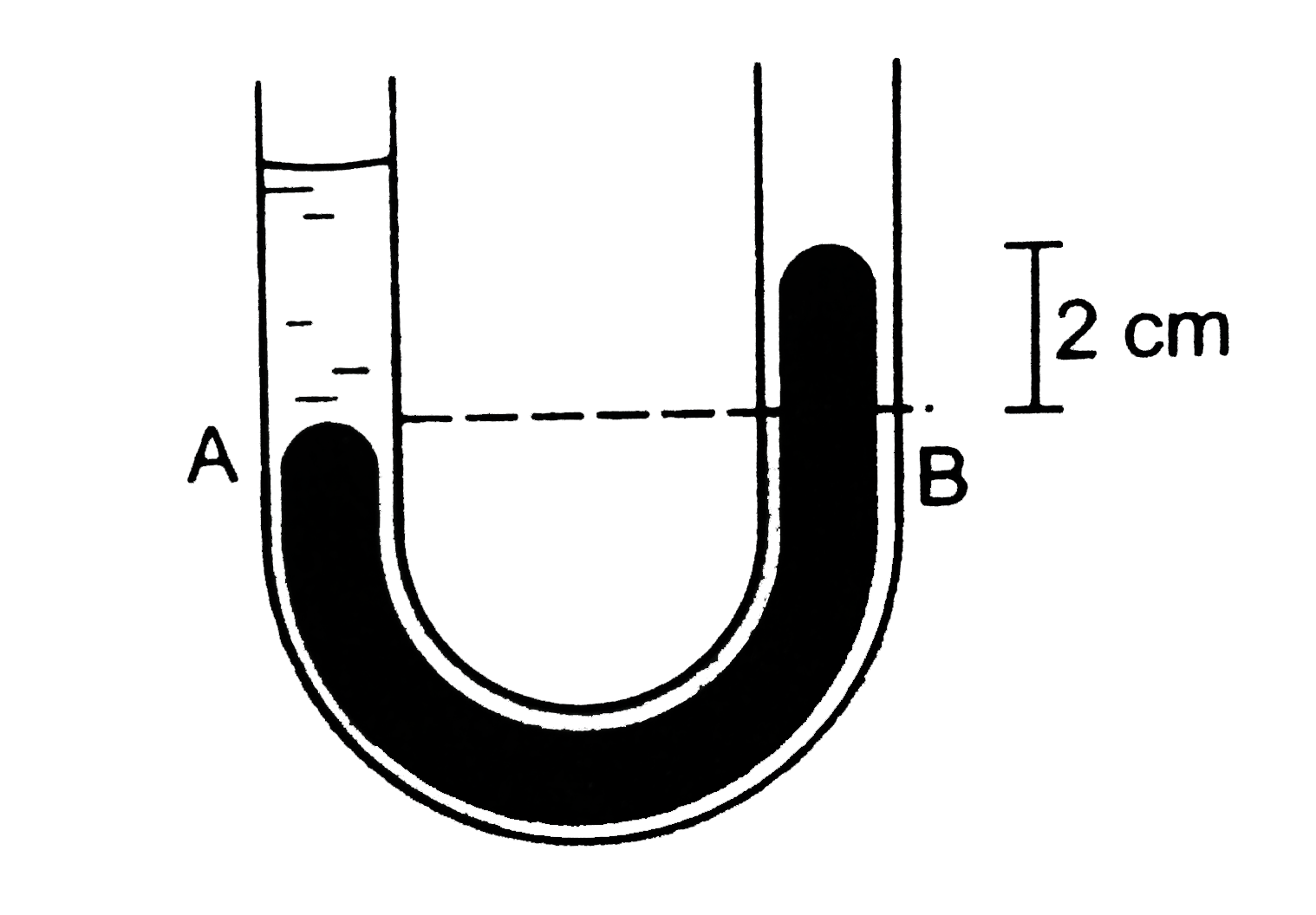 ,
,
View Solution
