A wooden block of mass 0.5 kg and density 800 kgm−3 is fastened to the free end of a vertical spring of spring constant 50 Nm−1 fixed at the bottom. If the entire system is completely immersed in water, find a. the elongation (or compression) of the spring in equilibrium and b. the time period of vertical oscillations of the block when it is slightly depressed and released.Solution in Tamil
The correct Answer is:A, B, C
Given m = 5kg, P=800kgm3,k=50Nm
a. From the free body diagram
[hereVρg>mg. So, elongation will be there]
mg=kX+Vρug
→(0.5)x(10+50x(X))
=(0.5500)×103×(10)
→50x=(0.5)×(10)×((108)−1)
→50x=(54)
→x=(5200)
=x=2.5cm
b. since the system is inside water only kx unbalance force will be the driving force for SHM. There is no change in buoyant force
So, ma=kx
→a=kxm
→w2x=kxm
→(2pT)2=km
→T=2π√mk
=2π×√(0.550)=π5sec
Topper's Solved these Questions
Similar Questions
Find the accelerationof the moon with respect to the eath from the following data, Distance between the earth and the moon =3.85×105 km and the time taken by the moon to complete one revolution around the earth =27.3days
View SolutionA body slipping on a rough horizontal plane moves wioth a deceleationof 4.0ms. What is cofficient of kineic friction between the block and the plane?
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
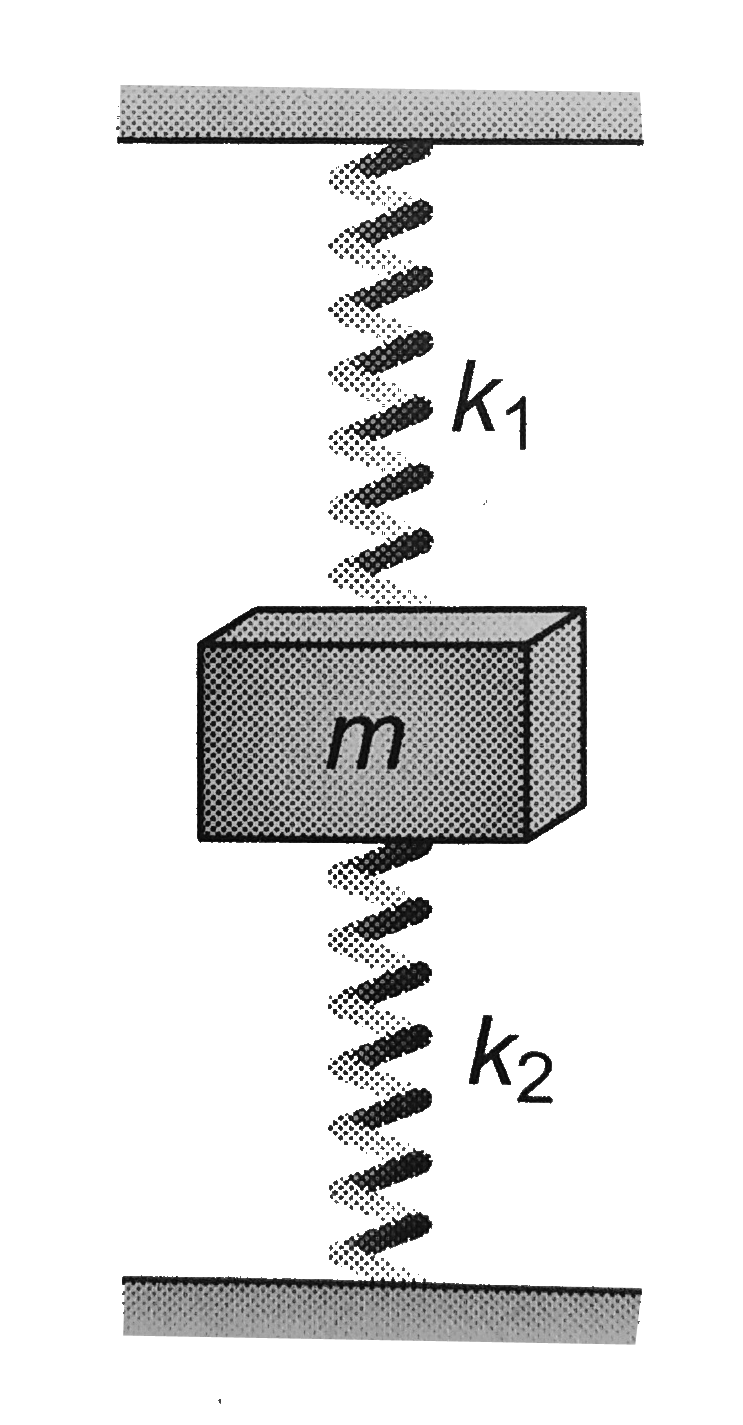
View SolutionIn the figure shown a block of masss m is atteched at ends of two spring The other ends of the spring are fixed The mass m is released in the vertical plane when the spring are released The velocity of the block is maximum when
View SolutionFigure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is
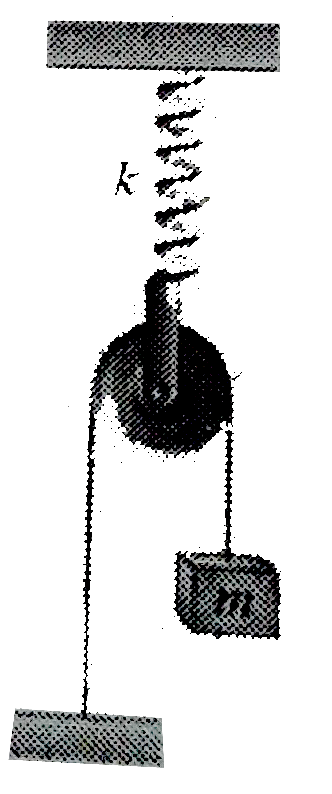
View SolutionA vertical spring-mass system with lower end of spring is fixed, made to undergo small oscillations. If the spring is stretched by 25cm , energy stored in the spring is 5J . Find the mass of the block if it makes 5 oscillations each second.
View SolutionA vertical spring-mass system with lower end of spring is fixed, made to undergo small oscillations. If the spring is stretched by 25cm, energy stored in the spring is 5J. Find the mass of the block if it makes 5 oscillations each second.
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

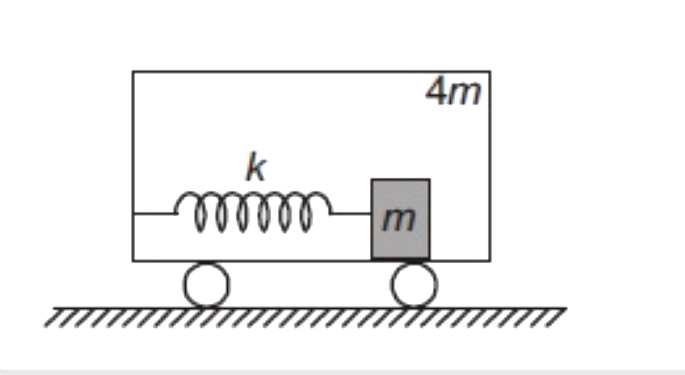
View SolutionA block of mass m is attached to a cart of mass 4m through spring of spring constant k as shown in the figure. Friction is absent everywhere. The time period of oscillations of the system, when spring is compressed and then released, is
View SolutionCalculate the period of oscillation of a block of mass 0.5 kg attached to a spring (spring constant 100Nm^(-1) ) at one end.
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA block of known mass is suspended from a fixed support through a ligh spring. Can you find the time period of vertical oscillation only by measuring the extension of the spring when the block is in equilibrium?
View Solutiona mass m is suspended at one end of a spring and the other end of the spring is fimly fixed on the celling. if the mass is slightly depressed and released it will execute oscillation. if this system is completely immersed in water then what happens to the oscillation?
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionA vertical spring-mass system with lower end of spring is fixed, made to undergo small oscillations. If the spring is stretched by 25cm, energy stored in the spring is 5J. Find the mass of the block if it makes 5 oscillations each second.
View SolutionA cube of wood of mass 0.5 kg and density 800 kg m^ (-3) is fastened to the free end of a vertical spring of spring constant k = 50 Nm^(-1) fixed at the bottom. Now, the entire system is completely submerged in water. The elongation or compression of the spring in equilibrium is (beta )/(2) cm . Find the value of beta . (Given g = 10 ms ^(-2) )
View Solution
