Question

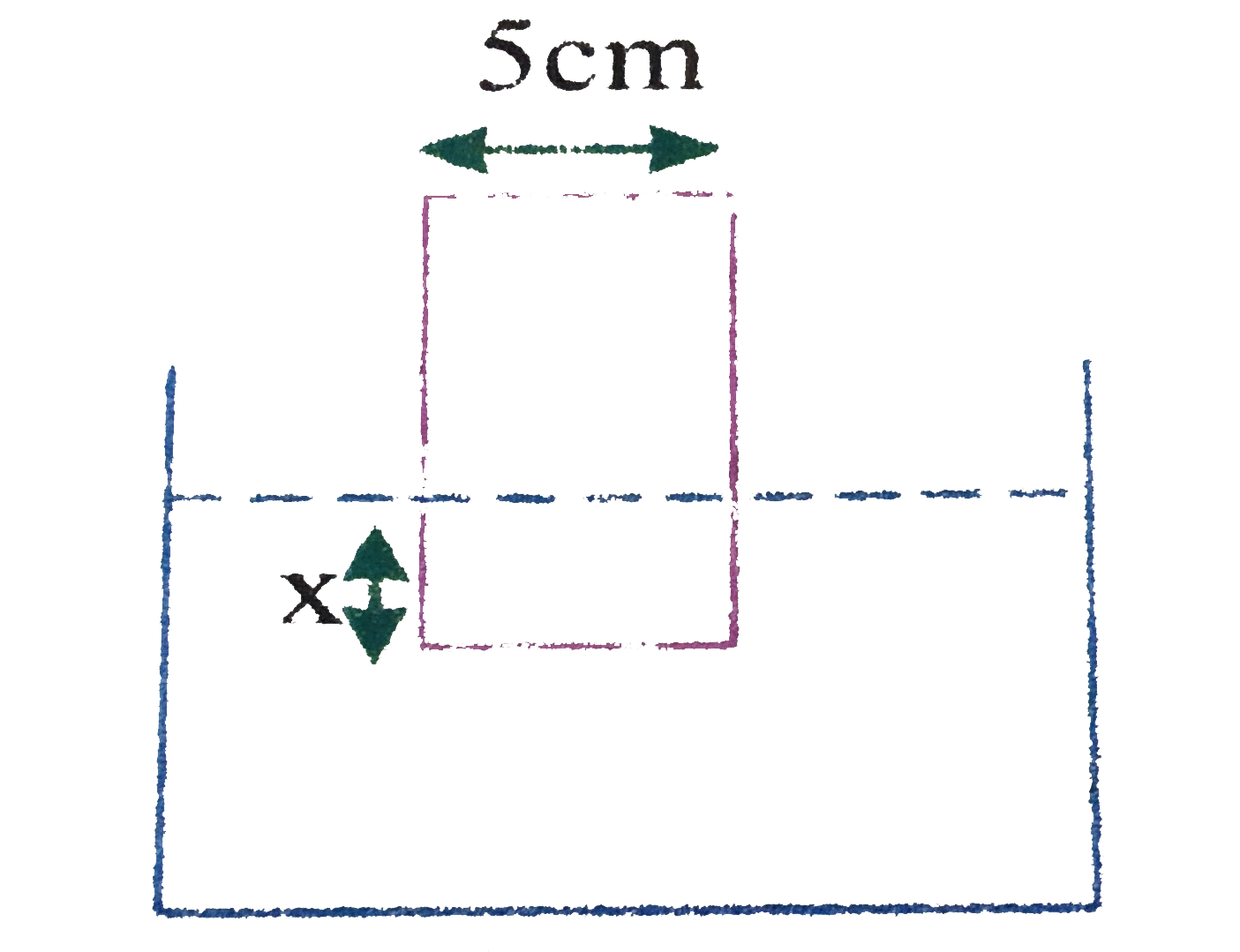
A cubical block of iron 5 cm on each side is floating on mercury in a vessel. (i) what is the height of the block above mercury level ?
(ii) Water is poured in the vessel unitl it just covers the iron block. What is the height of water column . density of mercur $13.6gm/c{m}^3$. Density of iron 7.2 $gm/c{m}^3$

Explanation

To solve the problem step by step, we will break it down into two parts as outlined in the question.

Part (i): Height of the block above mercury level

1. Determine the volume of the iron block:
The block is cubical with each side measuring 5 cm.
\( \text{Volume of the block} = \text{side}^3 = 5 \, \text{cm} \times 5 \, \text{cm} \times 5 \, \text{cm} = 125 \, \text{cm}^3 \)

2. Calculate the weight of the iron block:
The density of iron is given as 7.2 g/cm³.
\( \text{Weight of the block (mg)} = \text{Volume} \times \text{Density} \times g = 125 \, \text{cm}^3 \times 7.2 \, \text{g/cm}^3 \times g = 900 \, \text{g} \times g \)

3. Apply Archimedes' principle:
The weight of the block is equal to the upthrust (buoyant force) acting on it. The upthrust is given by the volume of the block submerged in mercury multiplied by the density of mercury.
\( \text{Upthrust} = \text{Volume submerged} \times \text{Density of mercury} \times g \)
Let \( V_s \) be the submerged volume. The total volume of the block is 125 cm³, so:
\( V_s = 125 \, \text{cm}^3 - V_{above} \)
where \( V_{above} \) is the volume of the block above the mercury level.

4. Set up the equation:
\( \text{Weight of the block} = \text{Upthrust} \)
\( 900 \, g = (125 - V_{above}) \times 13.6 \, g \)

5. Solve for \( V_{above} \):
\( 900 = (125 - V_{above}) \times 13.6 \)
Dividing both sides by 13.6:
\( \frac{900}{13.6} = 125 - V_{above} \)
\( 66.18 = 125 - V_{above} \)
Rearranging gives:
\( V_{above} = 125 - 66.18 = 58.82 \, \text{cm}^3 \)

6. Calculate the height above mercury:
The volume of the block above the mercury can be converted to height:
\( V_{above} = \text{Base area} \times \text{Height above mercury} \)
The base area of the cube is \( 5 \times 5 = 25 \, \text{cm}^2 \):
\( 58.82 = 25 \times h \)
Solving for \( h \):
\( h = \frac{58.82}{25} \approx 2.35 \, \text{cm} \)

Part (ii): Height of the water column

1. Set up the forces:
When water is poured until it just covers the iron block, we have two forces acting upwards: one from the mercury and one from the water. The total upthrust must equal the weight of the block.

2. Define variables:
Let \( y \) be the height of the water column. The height of the mercury column above the block will then be \( 5 - y \).

3. Write the equation for equilibrium:
\( \text{Weight of the block} = \text{Upthrust from mercury} + \text{Upthrust from water} \)
\( 900 = (5 - y) \times 13.6 + y \times 1 \)

4. Simplify the equation:
\( 900 = (5 \times 13.6 - 13.6y) + y \)
\( 900 = 68 - 12.6y \)
Rearranging gives:
\( 12.6y = 68 - 900 \)
\( 12.6y = -832 \)
\( y = \frac{-832}{12.6} \approx 2.53 \, \text{cm} \)

Final Answers:
(i) The height of the block above mercury level is approximately 2.35 cm.
(ii) The height of the water column is approximately 2.53 cm.