A tank contains water on top of mercury as shown in figure. A cubical block of side 10 cm is in equilibrium inside the tank. The depth of the block inside mercury is (RD of the material of block =8.56, RD of mercury =13.6)

6 cm
5 cm
7 cm
8 cm
The correct Answer is:A
Weight= upthrust from mercury + upthrust from water
∴ 10×8.56=(x×13.6)+(10−x)×10
Here x= depth inside mercury
Solving, we get
x=6 cm
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - B) Medical entrance special format question
19 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Match the columns
6 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.4
10 Videos
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A tank contains water and mercury as shown in . An iron cube of edge 6cm is in equilibrium as shown. What is the fraction of cube inside the mercury ? Given density of iron =7.7×103kgm−3 and density of mercury =13.6×103kgm−3.
View SolutionA tank contains water on top of mercury . A cube of iron, 60mm along each edge, is sitting upright in equilibrium in the liquids. Find how much of it is in each liquid. The densities of iron and mercury are 7.7×103kg/m3 and 13.6×103kg/m3 respectively

View Solution
Knowledge Check
A tank contains water and mercury as shown in figure. An iron cube of edge d=6 cm is in equilibrium as shown. (density of iron =7.8×103kg/m3, density of mercury =13.6×103kg/m3, density of water =103kgm3)(Neglect the atmospheric pressure)

Time period of small oscillations of block isA2π√dρFe(ρHg−ρW)gB2π√dρFe(ρHg+ρW)gC2π√dρFeρHggD2π√dρFeρwgThe solid as shown in the figure, is made up of cubical blocks each of side 1 cm. The number of blocks is
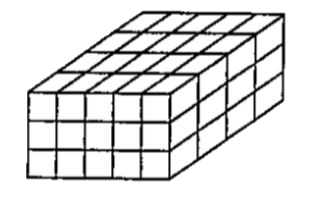 A52B60C72D48
A52B60C72D48A cubical block of side 10 cm floats at the interface of an oil and water. The pressure above that of atmosphere at the lower face of the block is
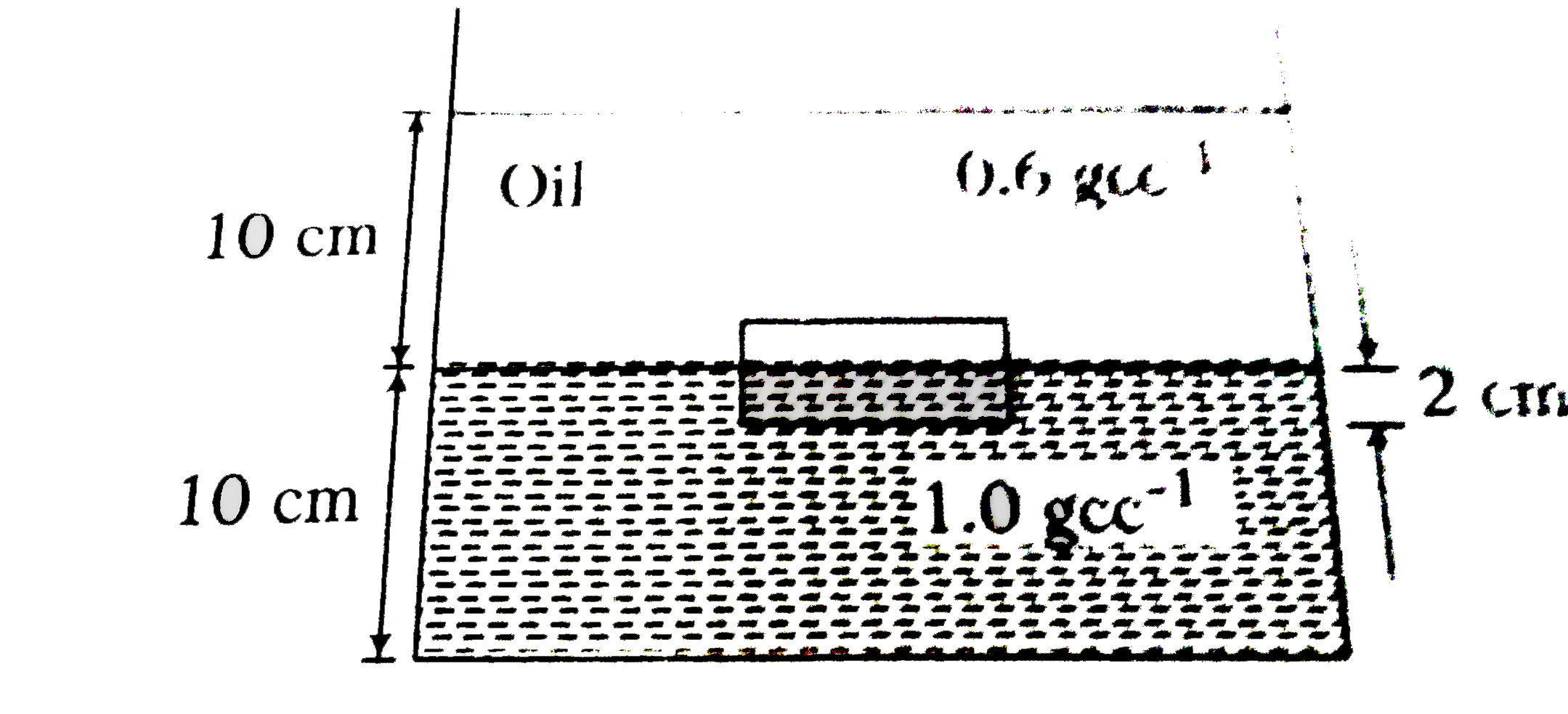 A200Nm−2B680Nm−2C400Nm−2D800Nm−2
A200Nm−2B680Nm−2C400Nm−2D800Nm−2
A container has a square cross-section of 10cm×10cm. A cubical ice block of side length 6 cm is floating in water in the container. Water level in the container is 6 cm high. The ice block is at a temperature of 0∘C and the water is at 16.15∘C. Assume that heat exchange take place between the ice block and water only. What length of ice block will remain submerged in water when the system reaches thermal equilibrium? Assume that the ice block maintains its cubical shape as it melts. Take - density of ice =0.9g/cc, density of water = 1.0g/cc
Specific heat capacity of water =1calg−1.∘C−1, Specific latent heat of fusion of ice =80calg−1
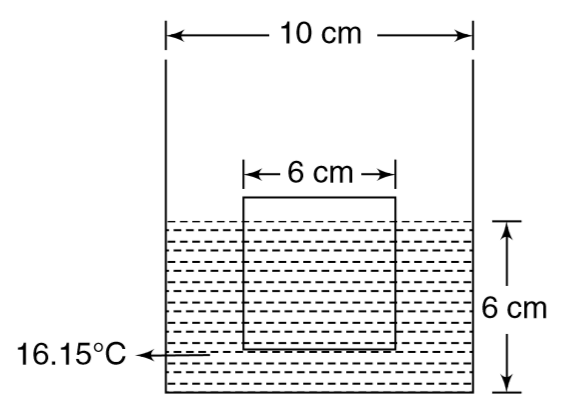
View SolutionA cubical metal block of edge 12 cm floats in mercry with one fifth of the height inside the mercury. Water poured till the surface of the block is just immersed in it. Find the height of the block is just immersed in it. Find the height of the water column to be poured. Specific gravity of mercury =13.6.
View SolutionA manometer reads the pressure of a gas in a enclosure as shown in figure(a) When some of the gas is removed by a pump, the manometer reads as in (b). The liquid used in the manometers is mercury and the atmospheric pressure is 76cm of mercury.
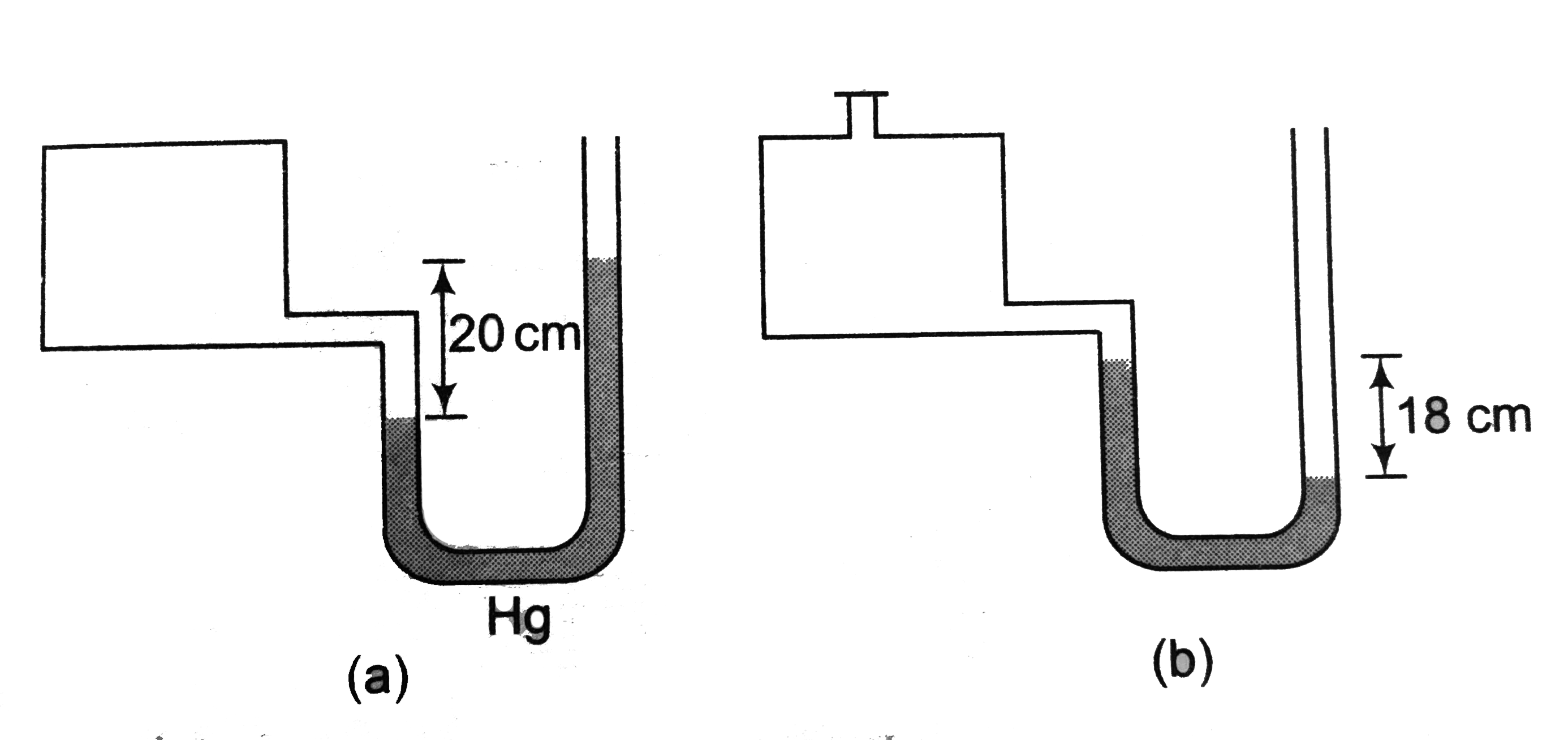
(i) Give the absolute and gauge pressure of the gas in the enclosure for cases (a) and (b) in units of cm of mercury .
(ii) How would the level change in case (b) if 13.6cm of water are poured into the right limb of the manometer?
View SolutionA two litre glass flask contains some mercury. It is found that at all temperatures the volume of the air inside the flask remains the same. The volume of the mercury inside the flask is (αfor glass =9×10−6/∘C,γ for mercury 1.8×10−4/∘C)
View SolutionA cubical block of steel of each side equal to 1 is floating on mercury in vessel. The densities of steel and mercury are ρs and ρm. The height of the block above the mercury level is given by
View Solution
