Two soap bubbles of radii r1 and r2 equal to 4 cm and 5 cm are touching each other over a common surface S1S2 (shown in figure). Its radius will be
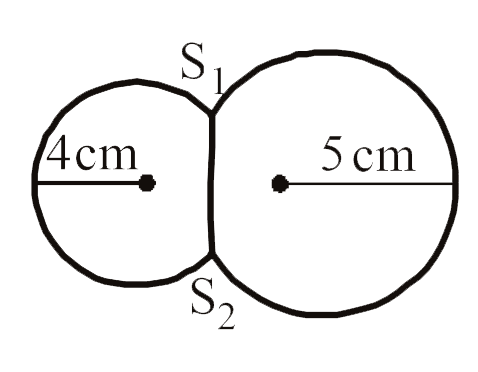
A
4 cm
B
20 cm
C
5 cm
D
4.5 cm
Video Solution
Text Solution
The correct Answer is:B
r=r1r2r1−r2=5×45−4=20cm
|
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - B) Medical entrance special format question
19 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Match the columns
6 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.4
10 Videos
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Knowledge Check
Prove that if two bubbles of radii r1 and r2(r1<r2) come in contact with each other then the radius of curvature of the common surface r=r1r2r2−r1
Ar2−r1Br2−r1r1r2Cr1r2r2−r1Dr2+r1Two soap bubbles each of radius r are touching each other. The radius of curvature of the common surface will be:
AinfiniteB2rCrDr/2Two soap bubbles of radii R1andR2 kept in atmosphere are combined isothermally to form a big bubble of radius R. The expression for surface tension will be
AP0(R3+R31+R32)4(R2+R21+R22)BP0(R31+R32−R3)4(R2−R21−R22)CP0(R31+R32−R3)D4P0(R31+R32−R3)
Two soap bubbles of radii 4cm and 6 cm are in contact with each other. What is the radius of the common boundary?
View SolutionTwo soap bubbles of radii 2 cm and 3 cm are brought in contact. Find the radius of curvature (in cm) of the contact surface.
View SolutionTwo soap bubbles of radii 2 cm and 4 cm join to form a double bubble in air, then radius of. curvature of interface is
View SolutionTwo soap bubble of radii R1 and R2 are kept in vacuum at constant temperature, the ratio of masses of air inside them, is
View SolutionUnder isothermal condition two soap bubbles of radii r1 and r2 coalesce to form a single bubble of radius r. The external pressure is p0. Find the surface tension of the soap in terms of the given parameters.
View Solution