A cubical block of steel of each side equal to 1 is floating on mercury in vessel. The densities of steel and mercury are . The height of the block above the mercury level is given by
The correct Answer is:B
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - B) Medical entrance special format question
19 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Match the columns
6 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.4
10 Videos
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A cubical block of iron 5 cm on each side is floating on mercury in a vessel. (i) what is the height of the block above mercury level ?
(ii) Water is poured in the vessel unitl it just covers the iron block. What is the height of water column . density of mercur 13.6gm/cm3. Density of iron 7.2 gm/cm3
View Solution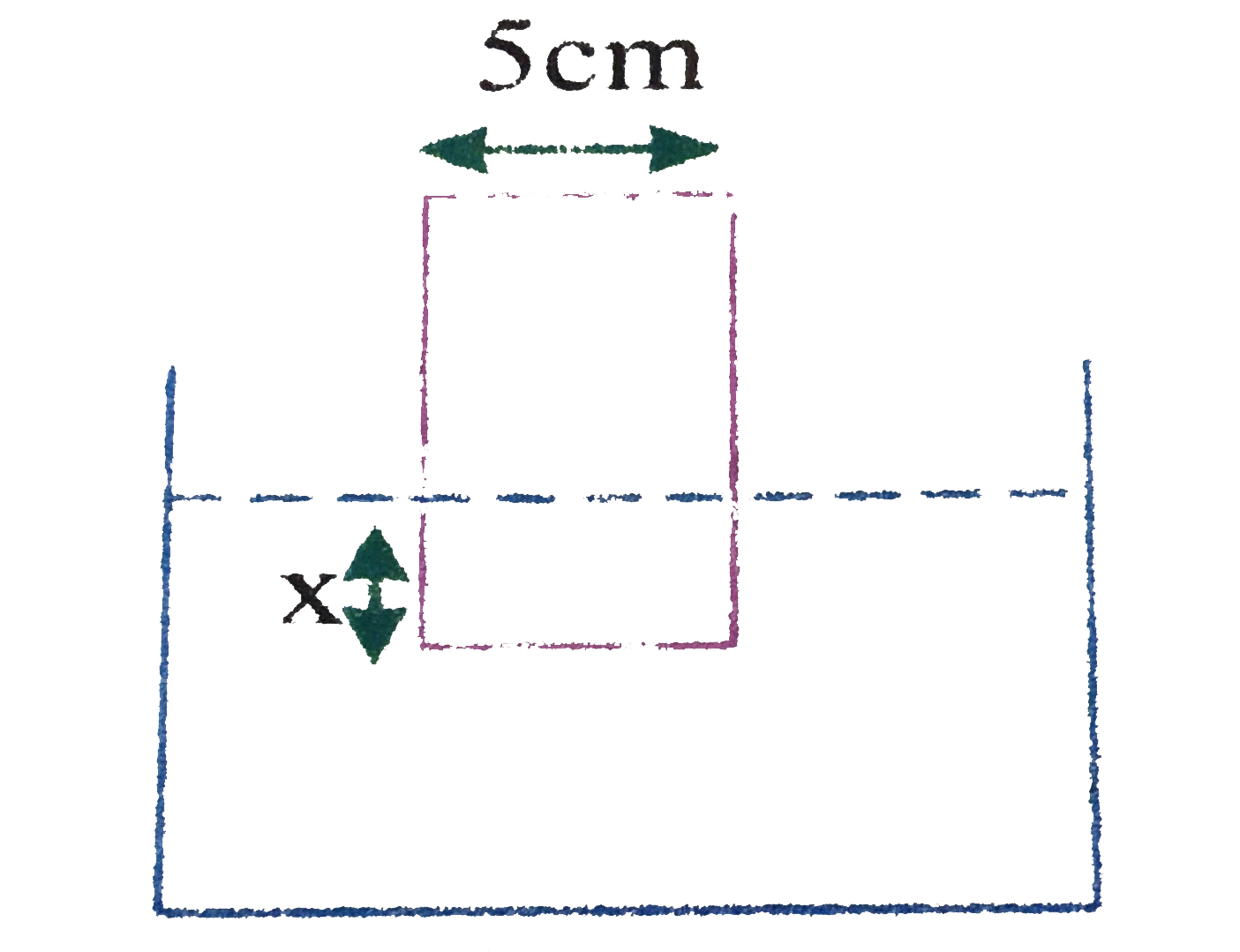
A cubical block of iron of side 5 cm is floating in mercury taken in a vessel. What is the height of the block above mercuery level.
(ρHg=13.6g/cm3,ρFe=7.2g/cm3)
View Solution
Knowledge Check
A steel ball floats on mercury because?
AMercury does not allow any metal ball to sink itBMercury is also a metal in the liquid formCThe density of mercury is higher than that of steelDA steel ball can be made to float on any liquid by suitable adjustmentA block of density ρ floats in a liquid with its one third volume immersed. The density of the liquid is
AρBρ3Cρ2D3ρA cube of iron whose sides are of length L, is put into mercury. The weight of iron cube is W. The density of irons is ρ1, that of mercury is ρM. The depth to which the cube sinks is given by the expression
AWL2ρIBWL2ρMCWL2ρIDWL2ρMg
A cubical metal block of edge 12 cm floats in mercry with one fifth of the height inside the mercury. Water poured till the surface of the block is just immersed in it. Find the height of the block is just immersed in it. Find the height of the water column to be poured. Specific gravity of mercury =13.6.
View Solution(i) A cubical metal block of side 10cm is floating in a vessel contatining mercury. The vesel has a square cross section of side length 15cm. Water is poured into the vessel so that the metal block just gets submerged. Calculate the mass of water that was poured into the vessel. It is given that relative density of the metal and mercury are 7.3 and 13.6 respectively.
(ii) In the last question, in place of water if we poured another liquid of relative density 'r' it was found that when the metal block ws just completely submerged it was no longer touching mercury. what is value of r?
View SolutionA cubical block of copper of side 10cm is floating in a vessel containing mercury. Water is poured into the vessel so that the copper block just gets submerged. The height of water column is
(ρHg=13.6g/cc,ρCu=7.3g/cc,ρwater=1gm/cc)
View SolutionA vessel is fileld with mercury to a height of 0.9m. Barometric height is 0.7m. mercury :
View SolutionA cylindrical block of the density ρ is partically immersed in a liwuid of density 3ρ. The plane surface of the block remains parallel to the surface of the liquid. The height of the block is 60m. The block perform SHM when displaced form its mean position [Use g=9.8m/s2]
View Solution
