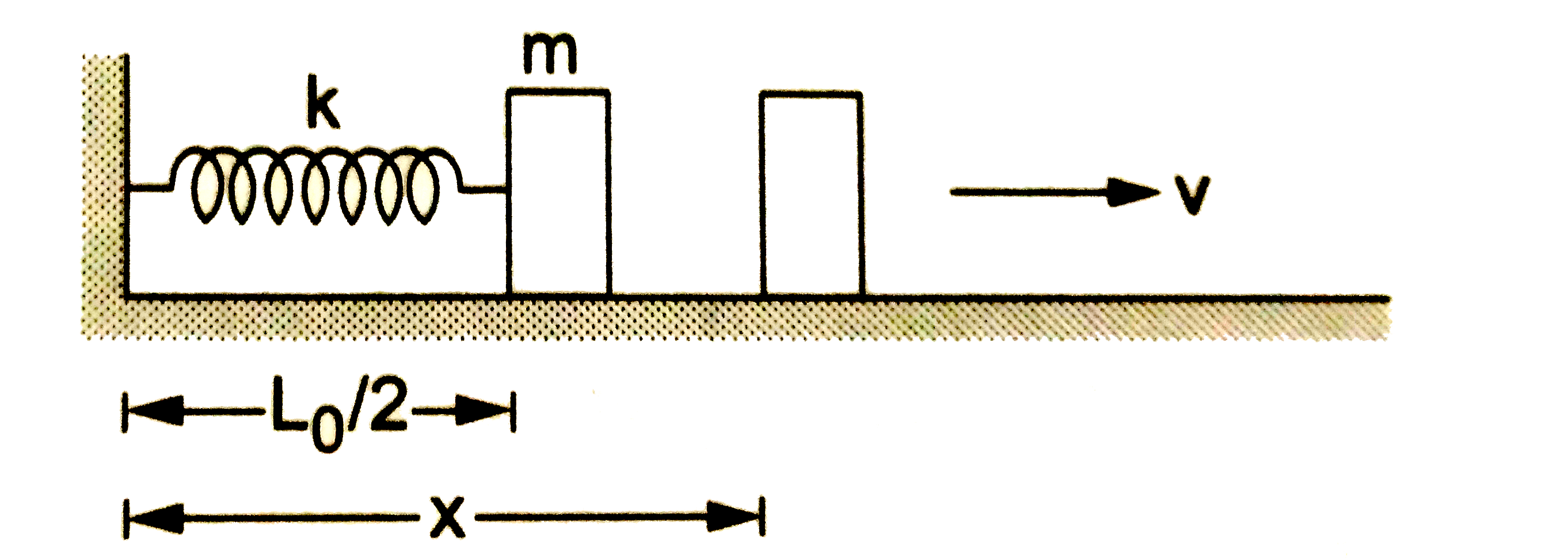
A block of mass m is pushed against a spring of spring constant k fixed at the end to a wall. The block can side on a frictionless table as shown in figure. The natural length of the spring is L0 and it is compressed ti half its natural length when the block is relesed. Find teh velocity of the block aa s function of its distance x from the wall .
 Solution in Tamil
Solution in Tamil
When the block is relesed, the spring pushes it towards right. The velocilty of the block increases till the spring acquires its N/Aturla length. Thereater, the block loses contct with the spring and movs with constant velocity.
Initially, the compression of the spring is L02, when the distance of the block from the wll becomes x, where x<L0 the compression is (L0−x). Using the principle of conversion of energy.
12k(L02)2=12k(L0−x)2)+12mv2
Solving this
v=√km[L204−(L0−x)2]12.
When the spring acquires its N/Atural lengthx=L0andv=√kmL02. Thereafter, the block contiues with this velocity.
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - WORK AND ENERGYEXERCISE - Question for Short Answer17videos
WORK AND ENERGY
- BOOK - HC VERMACHAPTER - WORK AND ENERGYEXERCISE - Objective -110videos
WORK AND ENERGY
- BOOK - HC VERMACHAPTER - WORK AND ENERGYEXERCISE - Exercises64videos
WORK AND ENERGY
- BOOK - HC VERMACHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Exercises57videos
WAVE MOTION AND WAVES ON A STRING
Similar Questions
When you lift a box from the floor and put it one an almirah the ptotential energy of the box increases, but thre is no change in its kinetic energy. Is it a violation of consevation of energy?
04:06View SolutionA heavy stone is thrown from a cliff of height h with a speed v. The stone will hit the ground with maximum speed if it is thrown
04:49View SolutionThe mass of a cyclist together with the bicycle is 90 kg. Calculate the work done by cyclist if the speed increases from 6km/h to 12 km/h.
01:11View SolutionA wave pulse passing on a string with speed of 40cms−1 in the negative x direction has its maximum at x=0 at t=0. Where will this maximum be located at t=5s?
08:46View SolutionA block of mass m is pushed against a spring of spring constant k fixed at one end to a wall.The block can slide on a frictionless table as shown in the figure. The natural length of the spring is L_0 and it is compressed to one fourth of natural length and the block is released.Find its velocity as a function of its distance (x) from the wall and maximum velocity of the block. The block is not attached to the spring.
01:23View SolutionIn the figure shown, a spring of spring constant K is fixed at on end and the other end is attached to the mass 'm' . The coefficient of friction between block and the inclined plane is mu . The block is released when the spring is in tis natural length. Assuming that the theta gt mu , the maximum speed of the block during the motion is.
06:02View SolutionA block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
 01:29View Solution
01:29View SolutionA block of mass m moving at a speed v_0 compresses a spring of spring constant k as shown in the figure. Find (a) the maximum compression of spring and (b) speed of the block when the spring is compressed to half of maximum compression.
06:01View SolutionA block ofmass m is attached with a spring in its natural length, of spring constant k. The other end A of spring is moved with a constant acceleration 'a' away from the block as shown in the figure -3.74 . Find the maximum extension in the spring. Assume that initially block and spring is at rest w.r.t ground frame:
01:43View SolutionA block Q of mass 2m is placed on a horizontal frictionless plane. A second block of mass m is placed on it and is connected to a spring of spring constant K, the two block are pulled by distance A. Block Q oscillates without slipping. The work done by the friction force on block Q when the spring regains its natural length is:
06:28View SolutionA block of mass m, attacted to a string of spring constant k, oscillates on a smooth horizontal table. The other end of the spring is fixed to a wall. The block has a speed v when the spring is at its natural length. Before coming to an instantaneous rest. If the block moves a distance x from the mean position, then
05:19View SolutionA block of mass m is placed on a smooth block of mass M = m with the help of a spring as shown in the figure. A velocity v_(0) is given to upper block when spring is in natural length. Find maximum compression in the spring.
05:57View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.
 06:02View Solution
06:02View Solutionm द्रव्यमान के एक गुटके से एक स्प्रिंग को दबाकर रखा जाता हैं । इस स्प्रिंग का स्प्रिंग स्थिरांक k हैं तथा स्प्रिंग का दूसरा सिरा दीवार में बँधा हैं । गुटका घर्षणरहित टेबुल पर फिसल सकता हैं । स्प्रिंग की स्वाभाविक लंबाई l0 हैं तथा उसे स्वाभाविक लंबाई के आधे तक दबाकर छोड़ा जाता हैं । दीवार से गुटके की दूरी के फलन के रुप में वेग का व्यंजक निकालें ।
 View Solution
View Solutionएक चिकनी क्षैतिज सतह वाली टेबुल पर एक ब्लॉक एक स्प्रिंग से बाँधकर आगे - पीछे दोलन करता हैं । स्प्रिंग का दूसरा किनारा टेबुल के एक बिंदु पर बाँधकर रखा गया हैं । स्प्रिंग का स्प्रिंग - नियतांक k हैं । जिस समय स्प्रिंग अपनी स्वाभाविक लंबाई में होता हैं , ब्लॉक की चाल v हैं । ब्लॉक टेबुल पर रुकने के पहले इस स्थिति से अधिकतम कितनी दूरी तक चलेगा ?
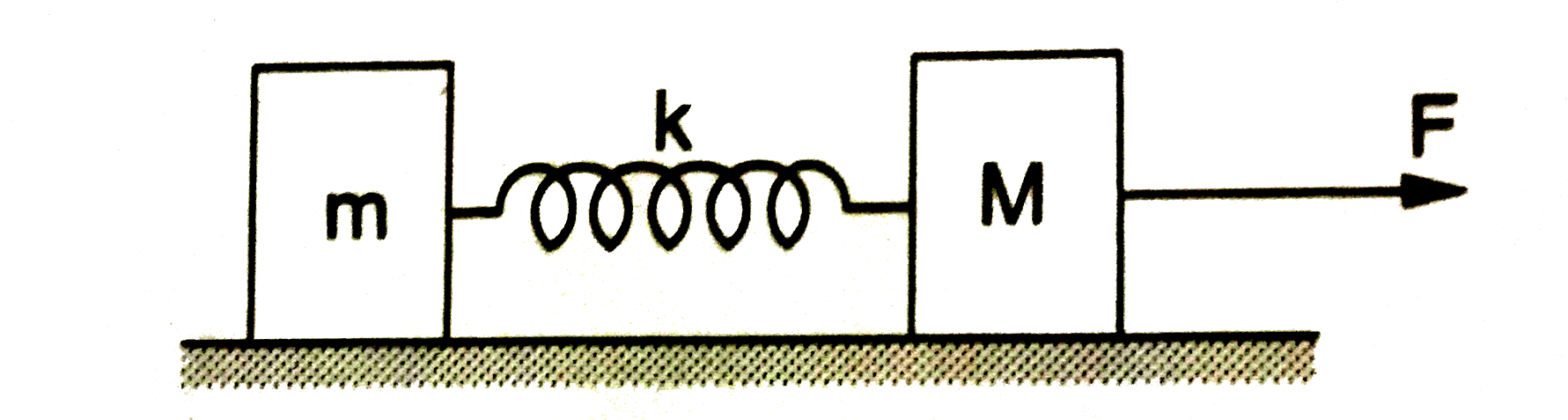
06:55View Solutionचित्र में दो गुटके दिखाए गए हैं जिनके द्रव्यमान m तथा M है। ये गुटके एक घर्षणरहित क्षैतिज सतह पर रखे हैं तथा k स्प्रिंग नियतांक वाले एक स्प्रिंग से जुड़े हैं। प्रारंभ में स्प्रिंग अपनी स्वाभाविक लंबाई में है तथा गुटके स्थिर हैं। अब एक अचर बल F, द्रव्यमान M वाले गुटके पर लगना प्रारंभ करता है। स्प्रिंग की लंबाई में अधिकतम वृद्धि निकालें।
 02:22View Solution
02:22View Solution
