Figure shows a loop the loop track of radius R. A car (without engine) starts from a platform at a distance h above the top of the loop and goes around the loop without falling off the track. Find the minimum value of h for a successful looping. Neglect friction.
 Solution in Tamil
Solution in Tamil
Suppose the speed of the car at the topmost point of the loop si v. Taking the gravitatioN/Al potential energy to be ero at the platform and assuming that the car starts with a negligible speed the conservation of energy shows
0=−mgh+12mv2
or, mv2=2mgh
where m is the mass of teh car. The car moving in a circle must have radial aceleration v2R at this instant. The force on the car are mg due to gravirty and N due to the contact with the tgrack. Both these forces are n radial direction at the top o the loop. Thus, from Newton's law
mg+N=mv2R
or, Mg+N=2mghR
For h to be minimum N should assume the minimum value which can be zero. Thus,
2mg(hmin)R=mgorhmin=R2
Topper's Solved these Questions
- WORK AND ENERGYBOOK - HC VERMACHAPTER - WORK AND ENERGYEXERCISE - Question for Short Answer
17 Videos
- WORK AND ENERGYBOOK - HC VERMACHAPTER - WORK AND ENERGYEXERCISE - Objective -1
10 Videos
- WORK AND ENERGYBOOK - HC VERMACHAPTER - WORK AND ENERGYEXERCISE - Exercises
64 Videos
- WAVE MOTION AND WAVES ON A STRINGBOOK - HC VERMACHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Exercises
57 Videos
Similar Questions
When you lift a box from the floor and put it one an almirah the ptotential energy of the box increases, but thre is no change in its kinetic energy. Is it a violation of consevation of energy?
View SolutionA heavy stone is thrown from a cliff of height h with a speed v. The stone will hit the ground with maximum speed if it is thrown
View SolutionThe mass of a cyclist together with the bicycle is 90 kg. Calculate the work done by cyclist if the speed increases from 6km/h to 12 km/h.
View SolutionA wave pulse passing on a string with speed of 40cms−1 in the negative x direction has its maximum at x=0 at t=0. Where will this maximum be located at t=5s?
View SolutionThe block on the loop shown slides without friction. At what height from A it starts so that it passes against the track at B with a net upward force equal to its own weight? The radius of the loop is R.
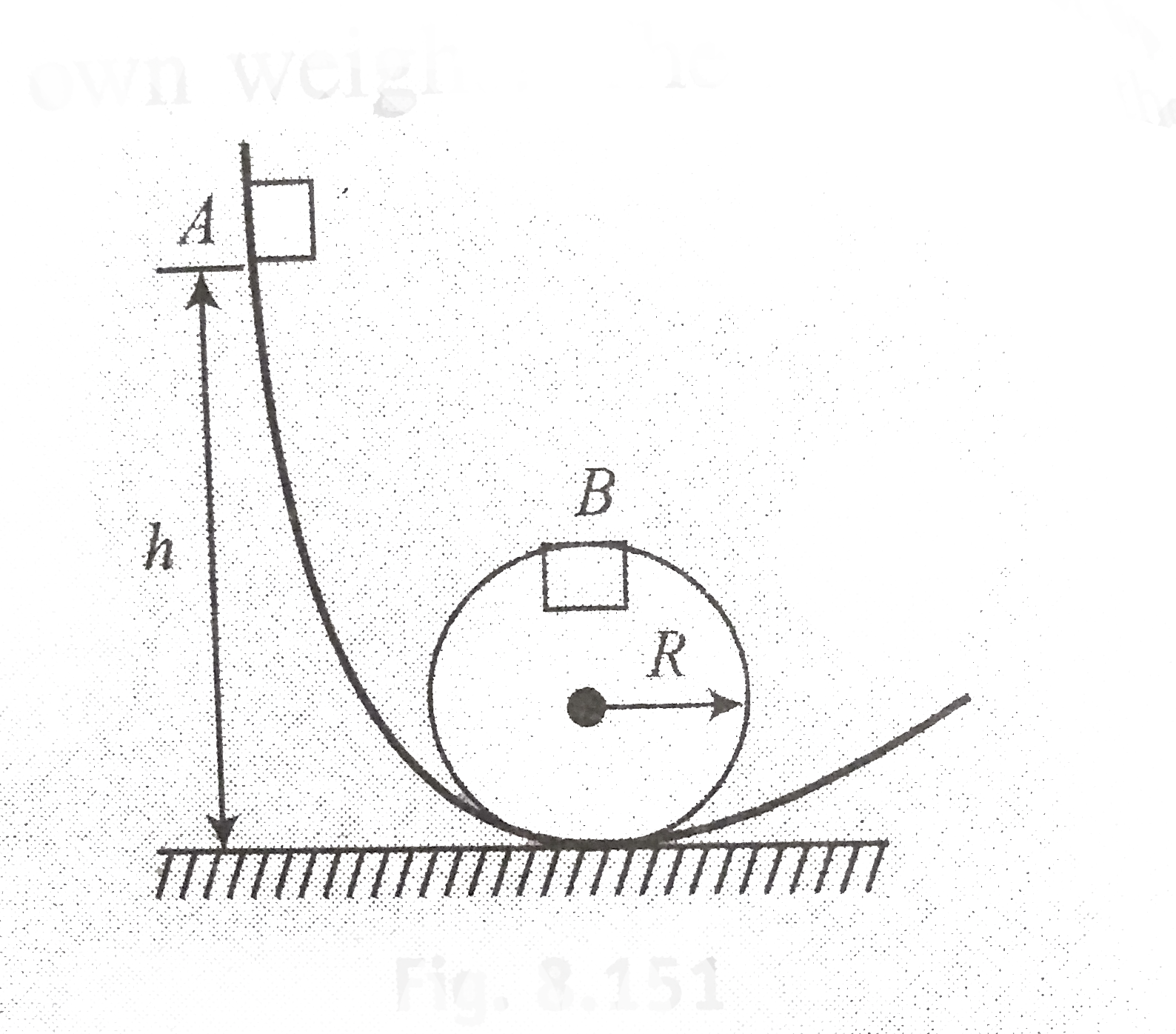
View SolutionA small of mass m starts from rest at the position shown and slides along the frictionless loop the loop track of radius R. What is the smallest value of y such that the object will slide without losing contact with the track?
View SolutionA frictionless track ABCDE ends in a circular loop of radius R . A body slides down the track from point A which is at a height h = 5 cm . Maximum value of R for the body to successfully complete the loop is
View SolutionA frictionless track ABCDE ends in a circular loop of radius R. A body slides down the track from point A which is at height h = 5cm. Maximum value of R for a body to complete the loop successfully is
View SolutionAn inclined track ends in a circular loop of radius r. From what height on the track a particle should be released so that it completes the loop, assuming there is no friction ?
View SolutionA small object of mass m starts from rest at the position shown and slides along the fricationless loop-the -loop track of radius R. What is the smallest value of y such that the object will slide without losing contact with the track?
View SolutionA frictionless tracke ABCDE ends in a circular loop of radius 'r' A body slides down the track from the point 'A' which is at a height h=10 cm . The maximum value of 'r' for the body to successful complete the loop is
View SolutionFigure shows a an incline which ends into a circular track of radius R. What should be the minimum value of height (h), so that the small object shown after release, is able to complete the loop. Neglect friction.
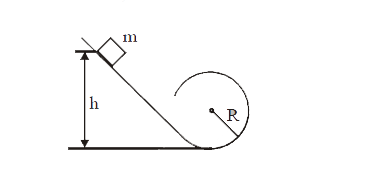
View SolutionA small solid sphere rolls without slipping along the track shown in figure. The sphere starts from rest from a height h above the bottom of a loop of radius R which is much larger than the radius of the sphere r. The minimum value of h for the sphere to complete the loop is:
View SolutionA body slides without friction from a height H = 60 cm and then loops the loop of radius R = 20 cm at the bottom of incline. The ratio of forces exerted on the body by the track at A,B and C are (g = 10 ms^(-2))
View SolutionIn looping the loop problem the highest through which the body falls is related to the radius of loop by h=__________
View SolutionA frictionless track ABCDE ends in a circular loop of radius R. A body slides down the track from point A which is at height h = 5cm. Maximum value of R for a body to complete the loop successfully is
View Solution
