A small solid sphere rolls without slipping along the track shown in figure. The sphere starts from rest from a height h above the bottom of a loop of radius R which is much larger than the radius of the sphere r. The minimum value of h for the sphere to complete the loop is:

2.1 R
2.3 R
2.7 R
2.5 R
The correct Answer is:C
At the topmost point of the loop minimum value of linear speed of centre of sphere should b:
v=√gR or translational kinetic energy =KT=12mv2=12mgR
In Case of pure rolling of a solid the ratio of rational to translational kinetic energy is
KRKT=25 ∴ Total kinetic energy at topmost point should be
∴K=5+25,KT=75(12mgR)=710mgR
Now from conservation of mechanical energy: 710mgR=mg(h−2R)∴h=2,7R
Similar Questions
Figure shows a loop track whose lower part ends into a circular track of radius R and centre O.
A small solid sphere of mass M rolls without slipping along the loop track from the end A at a height 6R from the bottom of the track. What is the horizontal force acting on the sphere, when it rises up to the point P in level with the centre O of the circular part ?

View Solution
A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.
View Solution
Knowledge Check
A solid sphere rolls down without slipping from rest on a 30∘ incline. Its linear acceleration is
A5g/7B5g/14C2g/3Dg/3A small block of mass m slides along a smooth frictional track as shown in the figure. If it starts from rest at P, what is the resultant force acting on it at Q?
 A1003mgB1009mgC2009mgD507mg
A1003mgB1009mgC2009mgD507mgA small sphere D of mass and radius rols without slipping inside a large fixed hemispherical radius R(>>r) as shown in figure. If the sphere starts from rest at the top point of the hemisphere normal force exerted by the small sphere on the hemisphere when its is at the bottom B of the hemisphere.
 .A107mgB177mgC57mgD75mg
.A107mgB177mgC57mgD75mg

A solid sphere of mass M and radius R is hit by a cue at a height h above the centre C. for what value of h the sphere will rool without slipping ?
View SolutionA solid sphere is rolling without slipping on rough ground as shown in figure. It collides elastically with another identical sphere at rest. There is no friction between the two spheres. Radius of each sphere is R and mass is m.

Linear velocity of first sphere after it again starts rolling without slipping is:
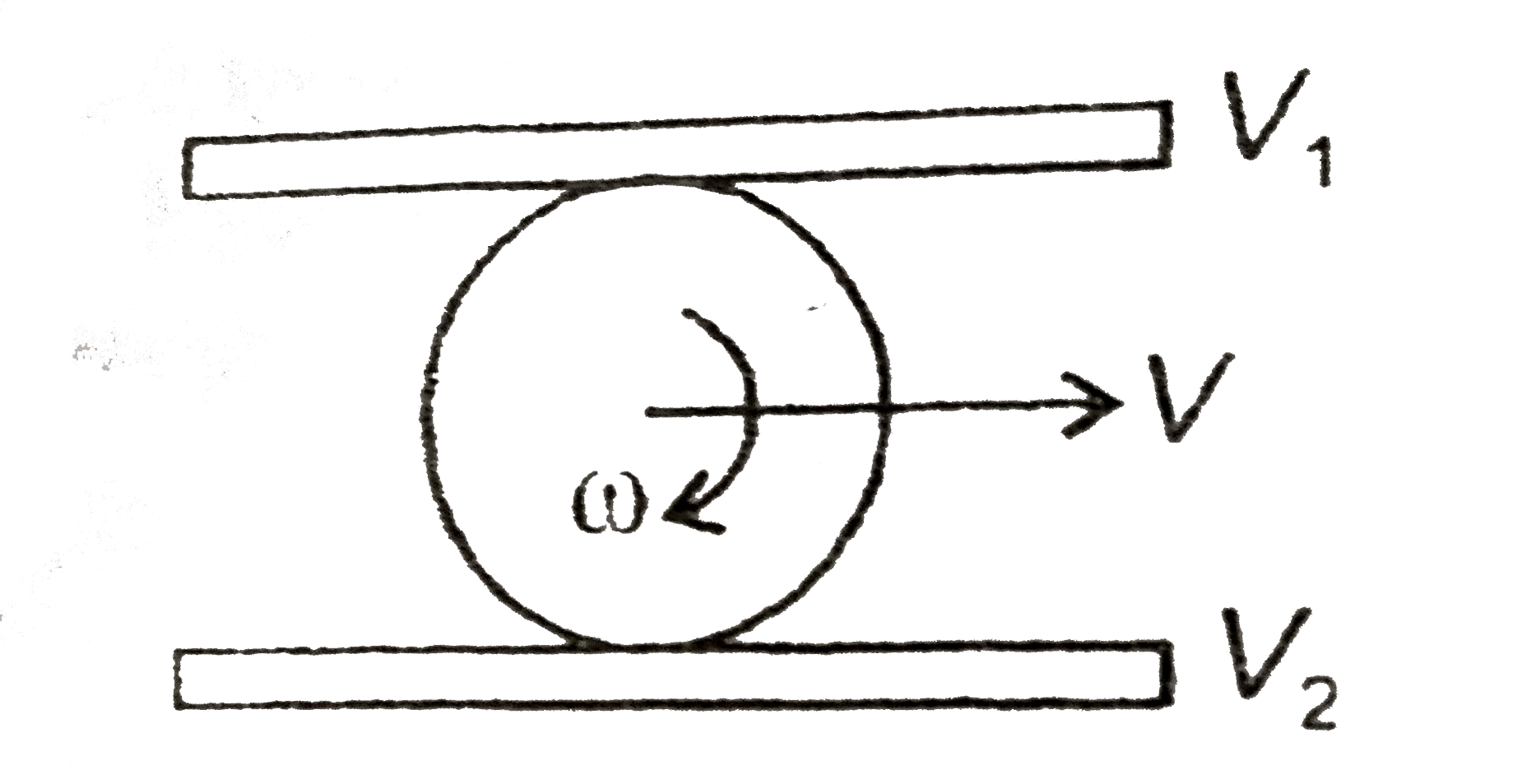
View SolutionA sphere of radius R rolls without slipping between two planks as shown in figure. Find
(a) Speed of centre of sphere
(b) Angular velocity of the sphere
View SolutionA small sphere S of radius ,r and mass m rolls without slipping, inside a large hemispherical bowl B of radius R as shown in figure. S starts from rest at the top point of the hemisphere
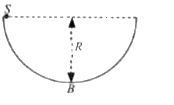
View SolutionA small solid sphere of radius r rolls down an incline without slipping which ends into a vertical loop of radius R. Find the height above the base so that it just loops the loop
View Solution
