AB and AC are tangents to a circle with centre O. A is the external point of the circle. The line AO intersect the chord BC at D. The measure of the ∠BDOis
60∘
90∘
45∘
75∘
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Understand the Configuration
We have a circle with center O and two tangents AB and AC drawn from an external point A. The line AO intersects the chord BC at point D. We need to find the measure of angle BDO.
Step 2: Identify Key Properties
Since AB and AC are tangents to the circle from point A, we know that:
- OA is the radius to the point of tangency, making angles OAB and OAC both equal to 90 degrees.
- The lengths of the tangents from a point outside the circle to the points of tangency are equal, i.e., AB = AC.
Step 3: Establish Congruent Triangles
We can observe two triangles:
- Triangle AOB
- Triangle AOC
Since:
- OA = OA (common side)
- AB = AC (tangent lengths)
- Angle OAB = Angle OAC = 90 degrees
By the criteria of congruence (RHS), we can conclude that:
- Triangle AOB is congruent to Triangle AOC.
Step 4: Analyze Angles in Congruent Triangles
From the congruence of triangles AOB and AOC, we have:
- Angle AOB = Angle AOC.
Step 5: Consider Triangles ABD and ACD
Now, we will look at triangles ABD and ACD:
- AD is a common side.
- AB = AC (from the tangents).
- Angle ADB = Angle ADC (as both angles subtend the same arc BC).
Thus, triangles ABD and ACD are also congruent by the criteria AAS (Angle-Angle-Side).
Step 6: Conclude the Measure of Angle BDO
From the congruence of triangles ABD and ACD, we have:
- Angle ADB = Angle ADC.
Let’s denote these angles as θ. Therefore:
- Angle ADB + Angle ADC = 180 degrees (since they are supplementary).
This gives us:
- 2θ = 180 degrees
- θ = 90 degrees.
Thus, angle BDO, which is equal to angle ADB, is also 90 degrees.
Final Answer
The measure of angle BDO is 90 degrees.
---
We have a circle with center O and two tangents AB and AC drawn from an external point A. The line AO intersects the chord BC at point D. We need to find the measure of angle BDO.
Since AB and AC are tangents to the circle from point A, we know that:
- OA is the radius to the point of tangency, making angles OAB and OAC both equal to 90 degrees.
- The lengths of the tangents from a point outside the circle to the points of tangency are equal, i.e., AB = AC.
We can observe two triangles:
- Triangle AOB
- Triangle AOC
- OA = OA (common side)
- AB = AC (tangent lengths)
- Angle OAB = Angle OAC = 90 degrees
- Triangle AOB is congruent to Triangle AOC.
From the congruence of triangles AOB and AOC, we have:
- Angle AOB = Angle AOC.
Now, we will look at triangles ABD and ACD:
- AD is a common side.
- AB = AC (from the tangents).
- Angle ADB = Angle ADC (as both angles subtend the same arc BC).
From the congruence of triangles ABD and ACD, we have:
- Angle ADB = Angle ADC.
- Angle ADB + Angle ADC = 180 degrees (since they are supplementary).
- 2θ = 180 degrees
- θ = 90 degrees.
The measure of angle BDO is 90 degrees.
Topper's Solved these Questions
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIV)
Explore 90 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:TRY YOURSELF
Explore 25 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XII)
Explore 90 Videos
- DISCOUNTBook:KIRAN PUBLICATIONChapter:DISCOUNTExercise:Test Yourself
Explore 10 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
Similar Questions
Knowledge Check
AB and AC are tangents to the circle with centre O. Then x equals.
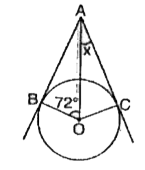 A22∘B18∘C20∘D36∘
A22∘B18∘C20∘D36∘The tangents are drawn at the extremities of diameter AB of a circle with centre P. If a tangent to the circle at the point C Intersects the other two tangents at Q and R, then the measure of the ∠QPR is
A45∘B60∘C90∘D180∘AB is a diameter of a circle with centre O. CD is a chord equal to the radius of the circle. AC and BD are produced to meet at P. Then the measure of ∠APB is:
A120∘B30∘C60∘D90∘
Two chords AB and CD of a circle with centre O intersect at point P within the circle. ∠AOC+∠BOD=?
View SolutionAB is the diameter of a circle with centre O. The tangent at a point C on the circle meets AB produced at Q. If ∠CAB=42∘, then what is the measure of ∠CQA?
AB एक वृत्त का व्यास है जिसका केंद्र O है | वत्त पर स्थित एक बिंदु C से गुजरने वाली स्पर्श रेखा AB से Q पर मिलती है | यदि ∠CAB=42∘ है, तो ∠CQA का मान क्या होगा ?
View SolutionA circle (with centre at O) is touching two intersecting lines AX and BY. The two points of contact A and B subtend an angle of 65∘ at any point C on the circumference of the circle. If P is the point of intersection for the two lines, then the measure of ∠APO is :
View SolutionA circle (with centre at O) is touching two intersecting lines AX and BY. The two points of contact A and B subtend an angle of 65∘ at any point C on the circumference of the circle. If P is the point of intersection for the two lines, then the measure of ∠APO is :
View SolutionAB is the chord of a circle with centre O and DOC is a line segment originating from a point D on the circle and intersecting AB produced at C such that BC = OD. If ∠BCD=20∘, then ∠AOD= ?
View Solution
