ΔABCis inscribed in a circle so that BC is diameter. The tangent at a point C intersects BA when produced at a point D. If ∠ABC=36∘ then the value of ∠ADCis
36∘
44∘
48∘
54∘
The correct Answer is:D
To solve the problem, we will follow these steps:
Step 1: Understand the given information
We have triangle ΔABC inscribed in a circle where BC is the diameter. The tangent at point C intersects line BA when extended at point D. We are given that ∠ABC=36∘.
Step 2: Identify the angles in the triangle
Since BC is the diameter of the circle, by the inscribed angle theorem, we know that ∠BAC is a right angle (90 degrees). This is because any angle inscribed in a semicircle is a right angle.
Step 3: Set up the equation for triangle ABC
In triangle ABC, we have:
- ∠ABC=36∘
- ∠BAC=90∘
- Let ∠ACB=θ.
Using the triangle sum property, we know that the sum of angles in a triangle is 180∘:
∠ABC+∠BAC+∠ACB=180∘
Substituting the known values:
36∘+90∘+θ=180∘
Step 4: Solve for θ
Now, we can solve for θ:
126∘+θ=180∘
θ=180∘−126∘=54∘
Thus, ∠ACB=54∘.
Step 5: Relate ∠ACB to ∠ADC
Since CD is a tangent to the circle at point C, we know that the angle between the tangent and the radius at the point of tangency is 90∘. Therefore, we have:
∠ACD=90∘
Step 6: Find ∠ADC
Now, we can find ∠ADC using the triangle ACD:
∠ACD+∠ACB+∠ADC=180∘
Substituting the known values:
90∘+54∘+∠ADC=180∘
144∘+∠ADC=180∘
∠ADC=180∘−144∘=36∘
Final Answer
The value of ∠ADC is 54∘.
We have triangle ΔABC inscribed in a circle where BC is the diameter. The tangent at point C intersects line BA when extended at point D. We are given that ∠ABC=36∘.
Since BC is the diameter of the circle, by the inscribed angle theorem, we know that ∠BAC is a right angle (90 degrees). This is because any angle inscribed in a semicircle is a right angle.
In triangle ABC, we have:
- ∠ABC=36∘
- ∠BAC=90∘
- Let ∠ACB=θ.
∠ABC+∠BAC+∠ACB=180∘
Substituting the known values:
36∘+90∘+θ=180∘
Now, we can solve for θ:
126∘+θ=180∘
θ=180∘−126∘=54∘
Thus, ∠ACB=54∘.
Since CD is a tangent to the circle at point C, we know that the angle between the tangent and the radius at the point of tangency is 90∘. Therefore, we have:
∠ACD=90∘
Now, we can find ∠ADC using the triangle ACD:
∠ACD+∠ACB+∠ADC=180∘
Substituting the known values:
90∘+54∘+∠ADC=180∘
144∘+∠ADC=180∘
∠ADC=180∘−144∘=36∘
The value of ∠ADC is 54∘.
Topper's Solved these Questions
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIV)
Explore 90 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:TRY YOURSELF
Explore 25 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XII)
Explore 90 Videos
- DISCOUNTBook:KIRAN PUBLICATIONChapter:DISCOUNTExercise:Test Yourself
Explore 10 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
Similar Questions
Knowledge Check
A, B and C are three points on a circle with centre O. The tangent at C meets BA produced to T. If ∠ATC=30∘ and ∠ACT=48∘, then what is the value of ∠AOB?
A78∘B96∘C102∘D108∘In figure , BOA is a diameter of circle and the tangent at point P meets BA produced at. T if ∠PBO=30∘ then ∠PTA=
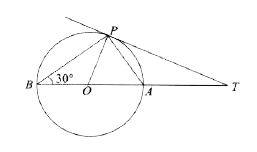 A30∘B60∘C90∘D45∘
A30∘B60∘C90∘D45∘AB is the diameter of a circle with centre O. The tangent at a point C on the circle meets AB produced at Q. If ∠CAB=42∘, then what is the measure of ∠CQA?
AB एक वृत्त का व्यास है जिसका केंद्र O है | वत्त पर स्थित एक बिंदु C से गुजरने वाली स्पर्श रेखा AB से Q पर मिलती है | यदि ∠CAB=42∘ है, तो ∠CQA का मान क्या होगा ?A5∘B7∘C17∘D6∘
In ΔABC,AB=AC.A circle is drawn with diameter AB and it intersects BC at D. Prove that D is the midpoint of BC.
View SolutionIn the figure, ray BC is tangent at point B and ray BA is secant. ∠ABC intercepts are AXB if m(arc AXB ) =130∘ then find the measure of ∠ABC.

View SolutionDraw the tangent, if two circle intersecting in two points.
View SolutionThe tangents are drawn at the extremities of diameter AB of a circle with centre P. If a tangent to the circle at the point C Intersects the other two tangents at Q and R, then the measure of the ∠QPR is
View SolutionThe radius of two concentric circles are 17cm and 10cm. A straight line ABCD intersects the larger circle at the point A and D and intersects the smaller circle at the points B and C. If BC = 12 cm, then the length of AD (in cm) is :
View Solution

