The radius of two concentric circles are 17cm and 10cm. A straight line ABCD intersects the larger circle at the point A and D and intersects the smaller circle at the points B and C. If BC = 12 cm, then the length of AD (in cm) is :
20
24
30
34
The correct Answer is:C
To find the length of AD in the given problem, we can follow these steps:
Step 1: Understand the Problem
We have two concentric circles with radii 17 cm (larger circle) and 10 cm (smaller circle). A straight line ABCD intersects the larger circle at points A and D, and the smaller circle at points B and C. We know that BC = 12 cm.
Step 2: Identify Key Points
Let O be the center of the circles. The line segment BC is perpendicular to the radius at point O, and it bisects the segment BC. Therefore, we can find the lengths of BE and CE:
- BE = CE = BC / 2 = 12 cm / 2 = 6 cm.
Step 3: Apply the Pythagorean Theorem
We can use the Pythagorean theorem in two right triangles: OBE and OAE.
1. For triangle OBE:
- OB (radius of smaller circle) = 10 cm
- BE = 6 cm
- OE (the perpendicular from O to BC) can be calculated as:
OE2+BE2=OB2OE2+62=102OE2+36=100OE2=64OE=8 cm
2. For triangle OAE:
- OA (radius of larger circle) = 17 cm
- AE (the segment we want to find) can be calculated as:
OE2+AE2=OA282+AE2=17264+AE2=289AE2=289−64AE2=225AE=15 cm
Step 4: Calculate Length of AD
Since AD is a chord of the larger circle, and OE bisects AD, we have:
- AE = ED = 15 cm
- Therefore, the total length of AD is:
AD=AE+ED=15+15=30 cm
Final Answer
The length of AD is 30 cm.
---
We have two concentric circles with radii 17 cm (larger circle) and 10 cm (smaller circle). A straight line ABCD intersects the larger circle at points A and D, and the smaller circle at points B and C. We know that BC = 12 cm.
Let O be the center of the circles. The line segment BC is perpendicular to the radius at point O, and it bisects the segment BC. Therefore, we can find the lengths of BE and CE:
- BE = CE = BC / 2 = 12 cm / 2 = 6 cm.
We can use the Pythagorean theorem in two right triangles: OBE and OAE.
- OB (radius of smaller circle) = 10 cm
- BE = 6 cm
- OE (the perpendicular from O to BC) can be calculated as:
OE2+BE2=OB2OE2+62=102OE2+36=100OE2=64OE=8 cm
- OA (radius of larger circle) = 17 cm
- AE (the segment we want to find) can be calculated as:
OE2+AE2=OA282+AE2=17264+AE2=289AE2=289−64AE2=225AE=15 cm
Since AD is a chord of the larger circle, and OE bisects AD, we have:
- AE = ED = 15 cm
- Therefore, the total length of AD is:
AD=AE+ED=15+15=30 cm
The length of AD is 30 cm.
Topper's Solved these Questions
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:TRY YOURSELF
Explore 25 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIII)
Explore 70 Videos
- DISCOUNTBook:KIRAN PUBLICATIONChapter:DISCOUNTExercise:Test Yourself
Explore 10 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
Similar Questions
The radii of two concentric circles are 17 cm and 25 cm. A straight line PQRS intersects the larger circle at the points P and S and intersects the smaller circle at the points Q and R. If RQ = 16 cm, then the length (in cm) of PS is
View SolutionIn Fig., the radii of two concentric circles are 13 cm and 8 cm. AB is diameter of the bigger circle. BD is the tangent to the smaller circle touching it at D. Find the length of AD.
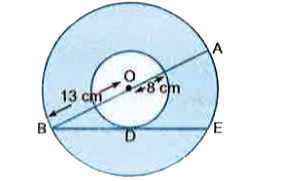
View Solution
Knowledge Check
In two concentric circles of radii 15 cm and 9 cm , then length of a biggest chord of the larger circle which is a tangent to the smaller circle is .
A24cmB20 cmC12 cmD10 cmThe radii of two concentric circle are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and the bigger circle at E. Point A is joined to D. Find the length of AD.
A20 cmB19 cmC18 cmD17 cmThe radius of two concentric circles are 9 cm and 15 cm. If the chord of the greater circle be a tangent to the smaller circle, then the length of that chord is
A24 cmB12 cmC30 cmD18 cm
The radii of two concentric circles are 13cm and 8cm, AB is a diameter of bigger circle. BD is a tangent to the smaller circle touching it at D. Find the length AD.
View SolutionTwo concentric circle of radii 13cm and 12 cm. What is the length of the chord of the larger circle which is tangent to the smaller circle?
View SolutionThe radii of two concentric circle are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and the bigger circle at E. Point A is joined to D. Find the length of AD.
View SolutionThe radius of the two concentric circles is 5 cm and 13 cm. The tangent to the smaller circle is the chord to the greater circle. What is the length (in cm) of that chord?
View SolutionThe radius of the two concentric circles is 5 cm and 13 cm. The tangent to the smaller circle is the chord to the greater circle. What is the length (in cm) of that chord?
View Solution
