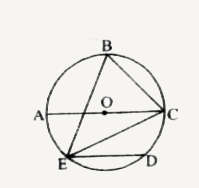
AC is the diameter of a circumcircle of ΔABC. Chord ED is par allel to the diameter AC. If ∠CBE=50∘, then the measure of ∠DECis
50∘
90∘
60∘
40∘
The correct Answer is:D
To solve the problem step by step, we will analyze the given information and apply the relevant geometric principles.
1. Identify the Given Information:
- AC is the diameter of the circumcircle of triangle ABC.
- Chord ED is parallel to the diameter AC.
- Angle CBE = 50°.
2. Determine Angle ABC:
- Since AC is the diameter of the circle, angle ABC is an inscribed angle that subtends the diameter. By the property of angles in a semicircle, angle ABC = 90°.
3. Calculate Angle ABE:
- We know that angle CBE = 50°.
- Since angle ABC = 90°, we can find angle ABE:
Angle ABE=Angle ABC−Angle CBE=90°−50°=40°.
4. Identify Angle DEC:
- We need to find angle DEC. Since ED is parallel to AC, we can use the property of alternate interior angles.
- Angle ABE (which we found to be 40°) is equal to angle DEC because they are alternate interior angles formed by the transversal BE intersecting the parallels AC and ED.
5. Conclusion:
- Therefore, angle DEC = angle ABE = 40°.
Final Answer:
Angle DEC=40°.
- AC is the diameter of the circumcircle of triangle ABC.
- Chord ED is parallel to the diameter AC.
- Angle CBE = 50°.
- Since AC is the diameter of the circle, angle ABC is an inscribed angle that subtends the diameter. By the property of angles in a semicircle, angle ABC = 90°.
- We know that angle CBE = 50°.
- Since angle ABC = 90°, we can find angle ABE:
Angle ABE=Angle ABC−Angle CBE=90°−50°=40°.
- We need to find angle DEC. Since ED is parallel to AC, we can use the property of alternate interior angles.
- Angle ABE (which we found to be 40°) is equal to angle DEC because they are alternate interior angles formed by the transversal BE intersecting the parallels AC and ED.
- Therefore, angle DEC = angle ABE = 40°.
Angle DEC=40°.
Topper's Solved these Questions
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:TRY YOURSELF
Explore 25 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIII)
Explore 70 Videos
- DISCOUNTBook:KIRAN PUBLICATIONChapter:DISCOUNTExercise:Test Yourself
Explore 10 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
Similar Questions
Knowledge Check
In the adjoining figure, chord ED is parallel to the diameter of the circle. If ∠CBE=65∘, then what is the value of ∠DEC ?
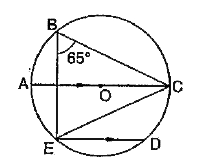 A35∘B55∘C45∘D25∘
A35∘B55∘C45∘D25∘DE is a tangent to the circumcircle of ΔABC at the vertex A such that DE∣∣BC. If AB=17cm, then the length of AC is equal to
A16.0cmB16.8cmC17.3cmD17cmIn the following figures, AB be diameter of a circle whose centre is O. If ∠AOE=150∘,∠DAO=51∘, then the measure of ∠CBE is-
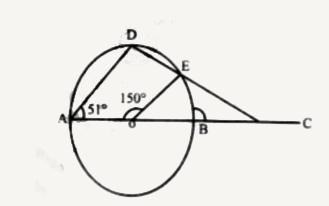 A115∘B110∘C105∘D120∘
A115∘B110∘C105∘D120∘
AC is the diameter of the circum-circle of the cyclic quadrilateral ABCD. IF ∠BDC=42∘ then what is ∠ACB equal to
View SolutionIn the following figures, AB be diameter of a circle whose centre is O. If ∠AOE=150∘,∠DAO=51∘, then the measure of ∠CBE is-

View SolutionThe tangent to the circumcircle of an isosceles ΔABC at A, in which AB= AC, is parallel to BC.
View SolutionIn the adjoining figure, O is the centre of a circle in which AB and CD are two diameters. Prove that AC| |BD and AD| |BC. If ∠OBD=50∘, then find the value of ∠AOC.

View SolutionAB is a diameter of a circle with centre O. CD is a chord equal to the radius of the circle. AC and BD are produced to meet at P. Then the measure of ∠APB is:
View Solution