XYandXZare tangents to a circle, STis another tangent to the circle at the point R on the circle, which intersects XYandXZat SandT respectively. If XY=15cmandTX=9cm, then RTis
4.5 cm
7.5 cm
6 cm
3 cm
The correct Answer is:C
To solve the problem step by step, we will use the properties of tangents to a circle.
1. Identify the Tangents: We have two tangents, XY and XZ, which are both drawn from point X to the circle. We are given that XY = 15 cm.
2. Use the Tangent Property: According to the property of tangents from an external point to a circle, the lengths of the tangents drawn from a point outside the circle to the points of tangency are equal. Therefore, we have:
XY=XZ=15 cm
3. Determine TX: We are given that TX = 9 cm.
4. Express XZ in Terms of TX and TZ: Since XZ can be expressed as:
XZ=TX+TZ
Substituting the known values:
15=9+TZ
5. Solve for TZ: Rearranging the equation gives us:
TZ=15−9=6 cm
6. Use the Tangent Property at Point T: Now, since TR is also a tangent from point T to the circle, we can apply the same tangent property. Therefore:
TZ=TR
Thus, we have:
TR=6 cm
7. Final Result: Therefore, the length of RT is:
RT=6 cm
Conclusion:
The length of RT is 6 cm.
XY=XZ=15 cm
XZ=TX+TZ
Substituting the known values:
15=9+TZ
TZ=15−9=6 cm
TZ=TR
Thus, we have:
TR=6 cm
RT=6 cm
The length of RT is 6 cm.
Topper's Solved these Questions
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIV)
90 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - TRY YOURSELF
25 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XII)
90 Videos
- DISCOUNTBOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself
10 Videos
- LCM AND HCF BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself
18 Videos
Similar Questions
Knowledge Check
Tangents to a circle at points P and Q on the circle intersect at a point R. If PQ= 6 and PR= 5 then the radius of the circle is
A133B4C154D165
CP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm, BC = 7cm, Then the length BR is :
View SolutionFrom an external point P, tangents PA and PB are drawn to a circle. CE is a tangent to the circle at D which intersect PA and PB at point E and C respectvely. If AP=15 cm, find the permeter of the △PEC.
View SolutionPQ and RS are common tangents of two circles intersection at A and B. AB, when produced both sides, meet the tangents PQ and RS at x and y, respectively. If AB = 3 cm, xy = 5 cm, then PQ (in cm) will be.
View SolutionA tangent to a circle intersects it in _________ points.
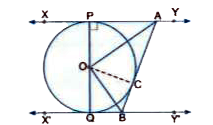
View SolutionIn Fig XY and X'Y' are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY and X'Y' at B , prove that ∠AOB=90∘
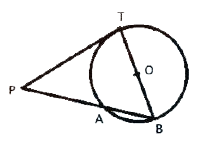
View SolutionIn the given figure, TB is a chord which passes through the centre of the circle. PT is a tangent to the circle at the point T on the circle. If PT = 10 cm, PA = 5 cm and AB = x cm. then the radius of the circle is:
View SolutionTwo circles are tangent internally at P and a chord, AB of the larger circle is tangent to the smaller circle at C. PB and PA cut the smaller circle at E and D, respectively. If AB = 15 cm, While PE = 2 cm and PD = 3 cm. Find AC
View Solution
