ABCD is a cyclic quadrilateral and O is the centre of the circle. If ∠COD=140∘and ∠BAC=40∘. then the value of ∠BCD is equal to
70∘
90∘
60∘
80∘
The correct Answer is:A
To solve the problem, we need to find the value of angle BCD in the cyclic quadrilateral ABCD, given that angle COD = 140° and angle BAC = 40°.
1. Understanding Cyclic Quadrilateral:
A cyclic quadrilateral is a four-sided figure where all vertices lie on the circumference of a circle. In a cyclic quadrilateral, the sum of the opposite angles is 180°.
2. Identify Given Angles:
We are given:
- Angle COD = 140°
- Angle BAC = 40°
3. Finding Angle BCD:
Since angle COD is the angle at the center of the circle, the angle subtended by the same arc (CD) at the circumference (angle BCD) is half of angle COD.
Angle BCD=12×Angle COD=12×140°=70°
4. Finding Angle ACD:
Now, we need to find angle ACD. Since angle BAC = 40°, and we have found angle BCD = 70°, we can find angle ACD using the property of cyclic quadrilaterals:
Angle ACD=180°−Angle BAC−Angle BCD
Angle ACD=180°−40°−70°=70°
5. Finding Angle BCD Again:
Now, we can find angle BCD again using the property of angles in a cyclic quadrilateral:
Angle BCD+Angle ACD=180°
Since we already calculated angle ACD = 70°, we can confirm:
Angle BCD=180°−Angle ACD=180°−70°=110°
6. Final Calculation:
Thus, we find that:
Angle BCD=110°
Conclusion:
The value of angle BCD is 110°.
A cyclic quadrilateral is a four-sided figure where all vertices lie on the circumference of a circle. In a cyclic quadrilateral, the sum of the opposite angles is 180°.
We are given:
- Angle COD = 140°
- Angle BAC = 40°
Since angle COD is the angle at the center of the circle, the angle subtended by the same arc (CD) at the circumference (angle BCD) is half of angle COD.
Angle BCD=12×Angle COD=12×140°=70°
Now, we need to find angle ACD. Since angle BAC = 40°, and we have found angle BCD = 70°, we can find angle ACD using the property of cyclic quadrilaterals:
Angle ACD=180°−Angle BAC−Angle BCD
Angle ACD=180°−40°−70°=70°
Now, we can find angle BCD again using the property of angles in a cyclic quadrilateral:
Angle BCD+Angle ACD=180°
Since we already calculated angle ACD = 70°, we can confirm:
Angle BCD=180°−Angle ACD=180°−70°=110°
Thus, we find that:
Angle BCD=110°
The value of angle BCD is 110°.
Topper's Solved these Questions
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XI)
Explore 22 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XII)
Explore 90 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-IX)
Explore 5 Videos
- DISCOUNTBook:KIRAN PUBLICATIONChapter:DISCOUNTExercise:Test Yourself
Explore 10 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
Similar Questions
Knowledge Check
ABCD is a quadrilateral inscribed in a circle with centre O. If ∠COD=120∘ and ∠BAC=30∘, then ∠BCD is :
A75∘B90∘C120∘D60∘ABCD is a cyclic quadrilateral whose diagonals intersect at P. If AB=BC,∠DBC=70∘and∠BAC=30∘, then the measure of ∠PCD is :
A35∘B50∘C55∘D30∘ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠CAB=48∘, then what is the value (in degrees) of ∠ADC?
A52B77C138D142
In the adjoining figure, ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠APC=120∘, then find the value of ∠CAB.
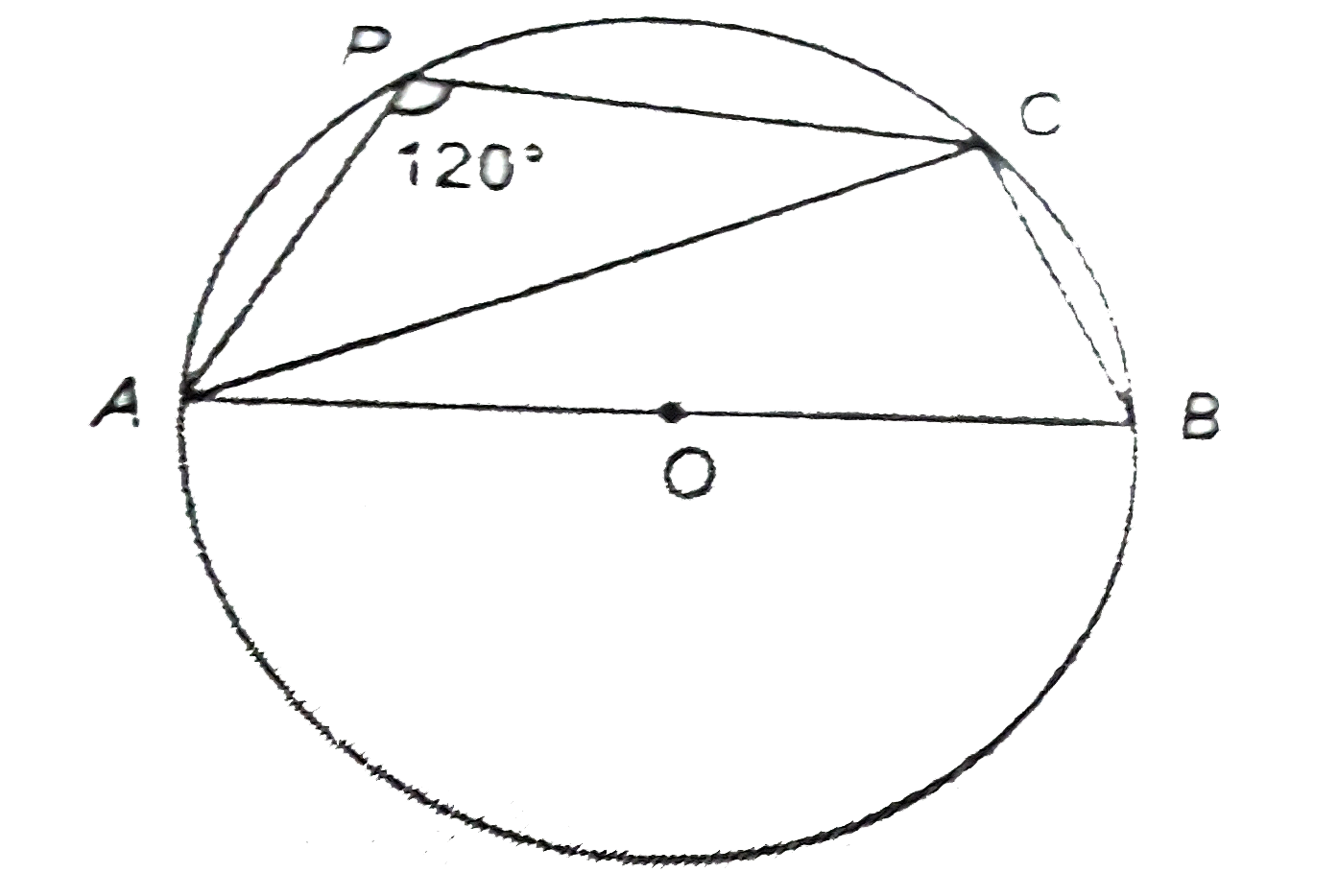
View SolutionIn the given figure if ∠DBC=70∘ and ∠BAC=40∘ then find the value of ∠BCD
View SolutionIn the given figure, ABCD is a cyclic quadrilateral; O is the centre of the circle.If ∠BOD=160∘, then find ∠BPD.
View SolutionIn Figure, ABCD is a cyclic quadrilateral. Find the value of x
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral whose side AB is the diameter of the circle . If ∠ADC=140∘ , then find the value of ∠BAC.

View Solution
