The diagonals AC and BD of a cyclic quadrilateral ABCD inter sect each other at the point P. Then, it is always true that
(a) BP.AB=CD.CP
(b) AP.CP=BP.DP
(c) AP.BP=CP.DP
(d) AP.CD=AB.CP
The correct Answer is:B
Step by step video, text & image solution for The diagonals AC and BD of a cyclic quadrilateral ABCD inter sect each other at the point P. Then, it is always true that by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XI)
22 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XII)
90 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-IX)
5 Videos
- DISCOUNTBOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself
10 Videos
- LCM AND HCF BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself
18 Videos
Similar Questions
The diagonals AC and BD of a cyclic quadrilateral ABCD interest at right angles at E (figure). A line l drawn through E and perpendicular to AB meets CD at F. Prove that F is the mid-point of CD.
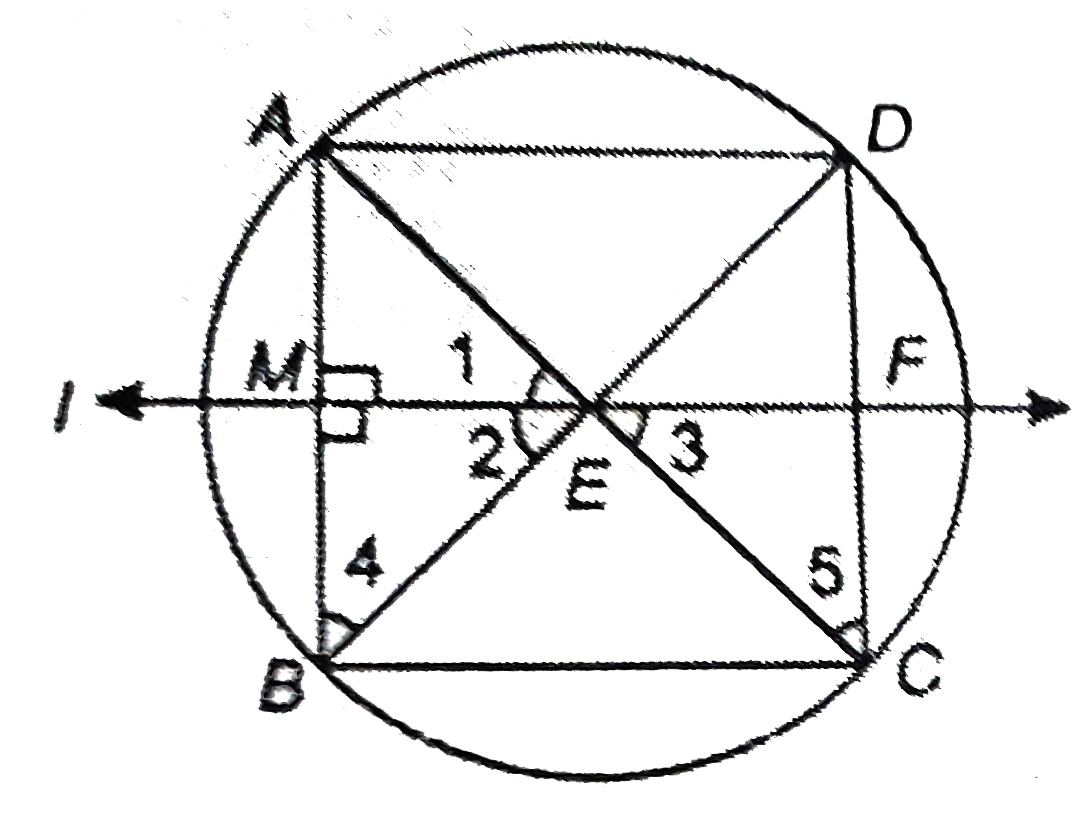
View SolutionThe diagonals of a quadrilateral ABCD intersect each other at the point O such that AOBO=CODO. Show that ABCD is a trapezium.
View Solution
Knowledge Check
The diagonals AC and BD of a cyclic quadrilateral ABCD intersect each other at the point P. Then,it is always true that
AAP. CP = BP. DPBAP.BP = CP. DPCAP. CD = AB. CPDBP. AB = CD.CPThe diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC=32∘and∠AOB=70∘, then ∠DBC is equal to
A24∘B86∘C38∘D32∘The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC=32∘and∠AOB=70∘, find ∠DBC.
A35∘B38∘C40∘D45∘
The diagonal of a quadrilateral ABCD intersect each other at the point D such that AOBO=CODO. Show that ABCD is a trapezium.
View SolutionThe diagonals AC and BD of a quadrilateral ABCD intersect at point 'O'. If BO = OD, then prove that the areas of ΔABCandΔADC are equal
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show thatar (APB) × ar (CPD) = ar (APD) × ar (BPC).
View SolutionThe diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC=32∘and∠AOB=70∘, then ∠DBC is equal to
View SolutionThe diagonal BD of a quadrilateral ABCD bisects ∠Band∠D, then :
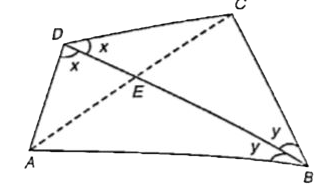
View Solution
