The length of the diagonal BD of the parallelogram ABCD is 18 cm. If PandQ are the centroid of the ΔABCandΔADC respectively then the length of the line segment PQ is
4 cm
6 cm
9 cm
12 cm
The correct Answer is:B
To find the length of the line segment PQ where P and Q are the centroids of triangles ABC and ADC respectively in the parallelogram ABCD with diagonal BD=18 cm, we can follow these steps:
1. Identify the Parallelogram and Diagonal:
- We have a parallelogram ABCD with diagonal BD measuring 18 cm.
2. Centroids of Triangles:
- The centroid P of triangle ABC divides the median AC in the ratio 2:1.
- The centroid Q of triangle ADC also divides the median AC in the ratio 2:1.
3. Length of the Diagonal:
- The entire length of diagonal BD is 18 cm.
4. Understanding the Ratio:
- The centroid divides the median into two segments, with the longer segment being twice the length of the shorter segment. Therefore, for the entire diagonal BD, we can express it in terms of units:
- The total length BD can be divided into 3 equal parts (since 2+1=3).
- Each part is 18 cm3=6 cm.
5. Finding Length of Segment PQ:
- The distance PQ is the distance between the two centroids P and Q.
- Since both centroids are 23 of the way from A to C along the diagonal AC, the distance PQ can be calculated as:
- PQ=2×length of one part=2×6 cm=12 cm.
Final Answer:
Thus, the length of the line segment PQ is 12 cm.
- We have a parallelogram ABCD with diagonal BD measuring 18 cm.
- The centroid P of triangle ABC divides the median AC in the ratio 2:1.
- The centroid Q of triangle ADC also divides the median AC in the ratio 2:1.
- The entire length of diagonal BD is 18 cm.
- The centroid divides the median into two segments, with the longer segment being twice the length of the shorter segment. Therefore, for the entire diagonal BD, we can express it in terms of units:
- The total length BD can be divided into 3 equal parts (since 2+1=3).
- Each part is 18 cm3=6 cm.
- The distance PQ is the distance between the two centroids P and Q.
- Since both centroids are 23 of the way from A to C along the diagonal AC, the distance PQ can be calculated as:
- PQ=2×length of one part=2×6 cm=12 cm.
Thus, the length of the line segment PQ is 12 cm.
Topper's Solved these Questions
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- X)
Explore 25 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XI)
Explore 22 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-VIII)
Explore 27 Videos
- DISCOUNTBook:KIRAN PUBLICATIONChapter:DISCOUNTExercise:Test Yourself
Explore 10 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
Similar Questions
ABCD is a parallelogram. E & F are centroid of triangles ABD and BDC respectively. Find the length of EF if length of diagonal AC = 12 cm.
View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively. Show that the line segments AF and EC trisect the diagonal BD.
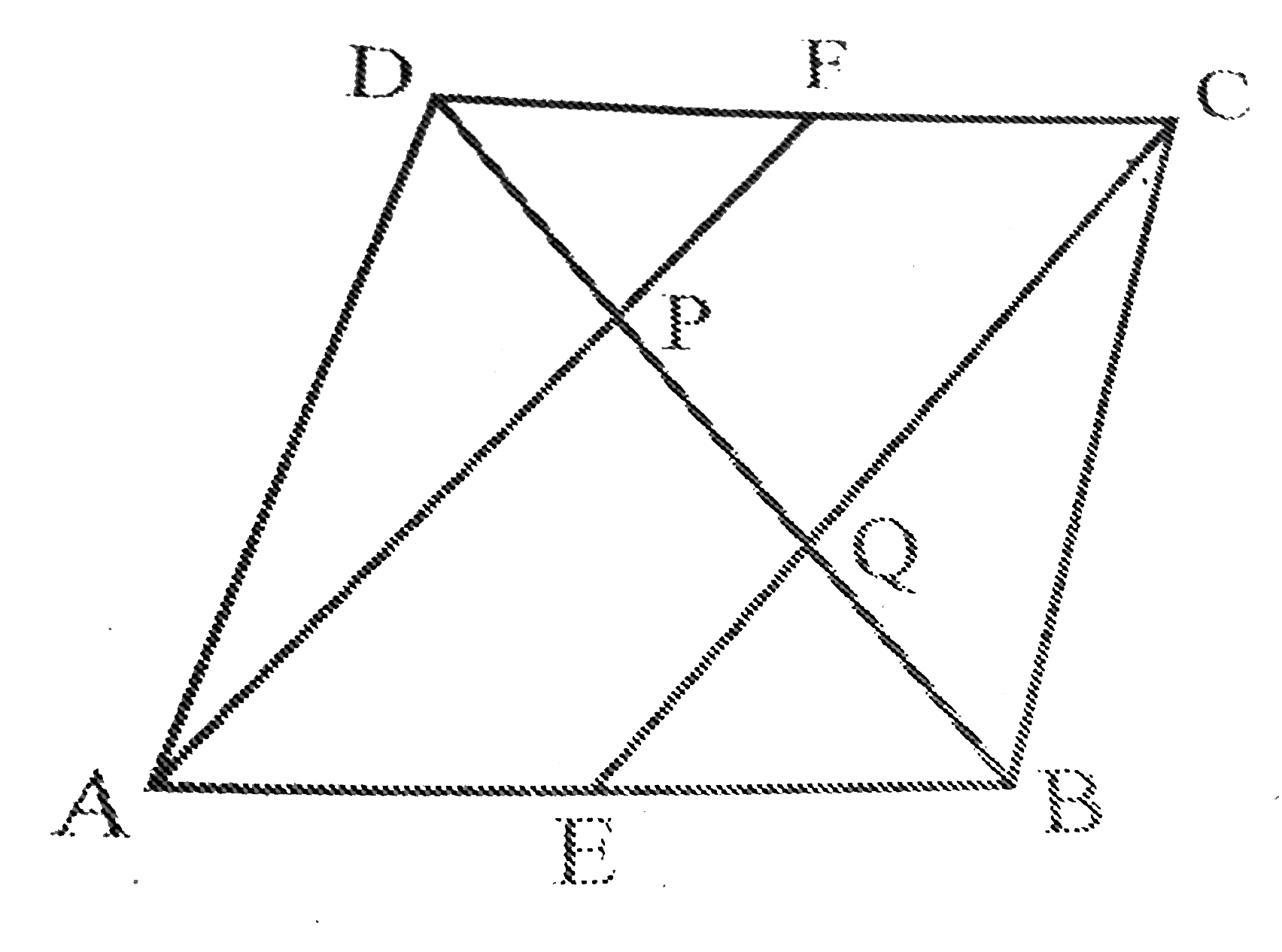
View Solution
Knowledge Check
If ABCD is a parallelogram in which P and Q are the centroids of ΔABDandΔBCD. then, PQ equals :
AAQBAPCBPDDQIf ABCD is a parallelogram in which P and Q are the centroids of ΔABDandΔBCD. then, PQ equals :
AAQBAPCBPDDQIn the given figure, ABCD is a parallelogram. E and F are the centroids of △ABD and △BCD, respectively.EF is equal to
AAEBBECCEDDE
In a parallelogram ABCD, E and F are the mid-points of sides BC and AD respectively. Show that the line segment BF and ED trisect the diagonal AC.
View SolutionIf the length of diagonal BD of a square ABCD is 4.8 cm, the area of the square ABCD is :
View SolutionIf the length of diagonal BD of a square ABCD is 4.8 cm, the area of the square ABCD is :
View SolutionOne of the diagonal of a parallelogram is 18 cm, whose adjacent sides are 16 cm and 20 cm respectively. What is the length of other diagonal?
View SolutionOne of the diagonal of a parallelogram is 18 cm, whose adjacent sides are 16 cm and 20 cm respectively. What is the length of other diagonal?
View Solution
