If ABCD is a parallelogram in which P and Q are the centroids of ΔABDandΔBCD. then, PQ equals :
AQ
AP
BP
DQ
The correct Answer is:B
To find the length of segment PQ in the parallelogram ABCD, where P and Q are the centroids of triangles ABD and BCD respectively, we can follow these steps:
Step 1: Understand the properties of centroids
The centroid of a triangle divides each median in the ratio 2:1. Therefore, if we consider triangle ABD, the centroid P divides the median AO (where O is the midpoint of BD) into segments AP and PO such that:
AP:PO=2:1
This means AP=2x and PO=x for some length x.
Step 2: Analyze triangle BCD
Similarly, for triangle BCD, the centroid Q divides the median CO (where O is the midpoint of AD) into segments CQ and OQ such that:
CQ:OQ=2:1
This means CQ=2y and OQ=y for some length y.
Step 3: Relate the segments
Since O is the midpoint of both diagonals AC and BD in the parallelogram, we have:
AO=OCandBO=OD
Thus, AO=OC implies that AP+PO=OQ+CQ.
Step 4: Set up the equations
From the previous steps, we have:
AP+PO=2x+x=3x
OQ+CQ=y+2y=3y
Since AO=OC, we can equate these two:
3x=3y⟹x=y
Step 5: Find PQ
Now, we can express PQ in terms of x:
PQ=PO+OQ=x+y=x+x=2x
Since AP=2x, we can conclude that:
PQ=AP
Conclusion
Thus, the length of segment PQ is equal to the length of segment AP.
Final Answer
PQ=AP
The centroid of a triangle divides each median in the ratio 2:1. Therefore, if we consider triangle ABD, the centroid P divides the median AO (where O is the midpoint of BD) into segments AP and PO such that:
AP:PO=2:1
This means AP=2x and PO=x for some length x.
Similarly, for triangle BCD, the centroid Q divides the median CO (where O is the midpoint of AD) into segments CQ and OQ such that:
CQ:OQ=2:1
This means CQ=2y and OQ=y for some length y.
Since O is the midpoint of both diagonals AC and BD in the parallelogram, we have:
AO=OCandBO=OD
Thus, AO=OC implies that AP+PO=OQ+CQ.
From the previous steps, we have:
AP+PO=2x+x=3x
OQ+CQ=y+2y=3y
Since AO=OC, we can equate these two:
3x=3y⟹x=y
Now, we can express PQ in terms of x:
PQ=PO+OQ=x+y=x+x=2x
Since AP=2x, we can conclude that:
PQ=AP
Thus, the length of segment PQ is equal to the length of segment AP.
PQ=AP
Topper's Solved these Questions
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.4
10 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.5
60 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.2
100 Videos
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 2
40 Videos
- HCF AND LCMBOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions
18 Videos
Similar Questions
In the given figure, ABCD is a parallelogram. E and F are the centroids of △ABD and △BCD, respectively.EF is equal to
View SolutionABCD is a parallelogram in which P and Q are midpoints of opposite sides AB and CD respectively (see figure). If AQ intersects DP at S and BQ intersects CP at R, show that:
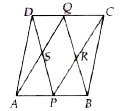
(i) APCQ is a parallelogram.
View Solution
Knowledge Check
If ABCD is a parallelogram in which P and Q are the centroids of ΔABDandΔBCD. then, PQ equals :
AAQBAPCBPDDQIn the given figure, ABCD is a parallelogram. E and F are the centroids of △ABD and △BCD, respectively.EF is equal to
AAEBBECCEDDEIn the given figure, ABCD is a parallelogram. E and F are the centroids of △ABD and △BCD, respectively.EF is equal to
AAEBBECCEDDE
ABCD is a parallelogram in which P and Q are midpoints of opposite sides AB and CD respectively (see figure). If AQ intersects DP at S and BQ intersects CP at R, show that:

DPBQ is a parallelogram
View SolutionABCD is a parallelogram in which P and Q are midpoints of opposite sides AB and CD respectively (see figure). If AQ intersects DP at S and BQ intersects CP at R, show that:

PSQR is a parallelogram.
View SolutionABCD is a parallelogram. Points P and Q are taken on the sides AB and AD respectively and the parallelogram PRQA is formed. If ∠C=45∘, find ∠R.
View SolutionThe length of the diagonal BD of the parallelogram ABCD is 18 cm. If PandQ are the centroid of the ΔABCandΔADC respectively then the length of the line segment PQ is
View SolutionABCD is a parallelogram. P and Q are mid points of BC & CD. Find the area of ΔAPQ if area of ΔABC is 12.
View Solution
