For the arrangement shown in figure, the spring is initially compressed by 3cm. When the spring is released the block collides with the wall and rebounds to compress the spring again.

(a) If the coefficient of restitution is 1√2 , find the maximum compression in the spring after collision.
(b) If the time starts at the instant when spring is released, find the minimum time after which the block becomes stationary.
Velocity of the block just before collision,
12mv20+12kx2=12kx20
or v0=√km(x20−x2)
here, x0=0.03m,x=0.01m,k=104N/m,m=1kg
∴v0=2√3m/s
After collision, v=ev0=(0.7)2√2=2m/s.
Maximum compression in the spring is
12kx2m=12kx2+12mv2
or xm=√x2+mkv2=√(0.01)2+1(2)2104=√5cm
Similar Questions
The system shown in the figure can move on a smooth surface. The spring is initially compressed by 6 cm and then released.

View Solution .
.
In the figure shown, AB=BC=2m. Friction coefficient everywhere is μ=0.2. Find the maximum compression of the spring.
View SolutionA ball is placed on a compressed spring. When the spring is released, the ball is observed to fly away.

What form of energy does the compressed spring possess ?
View SolutionA block of mass m strikes a light pan fitted with a vertical spring after falling through a distance h. If the stiffness of the spring is k, find the maximum compression of the spring.
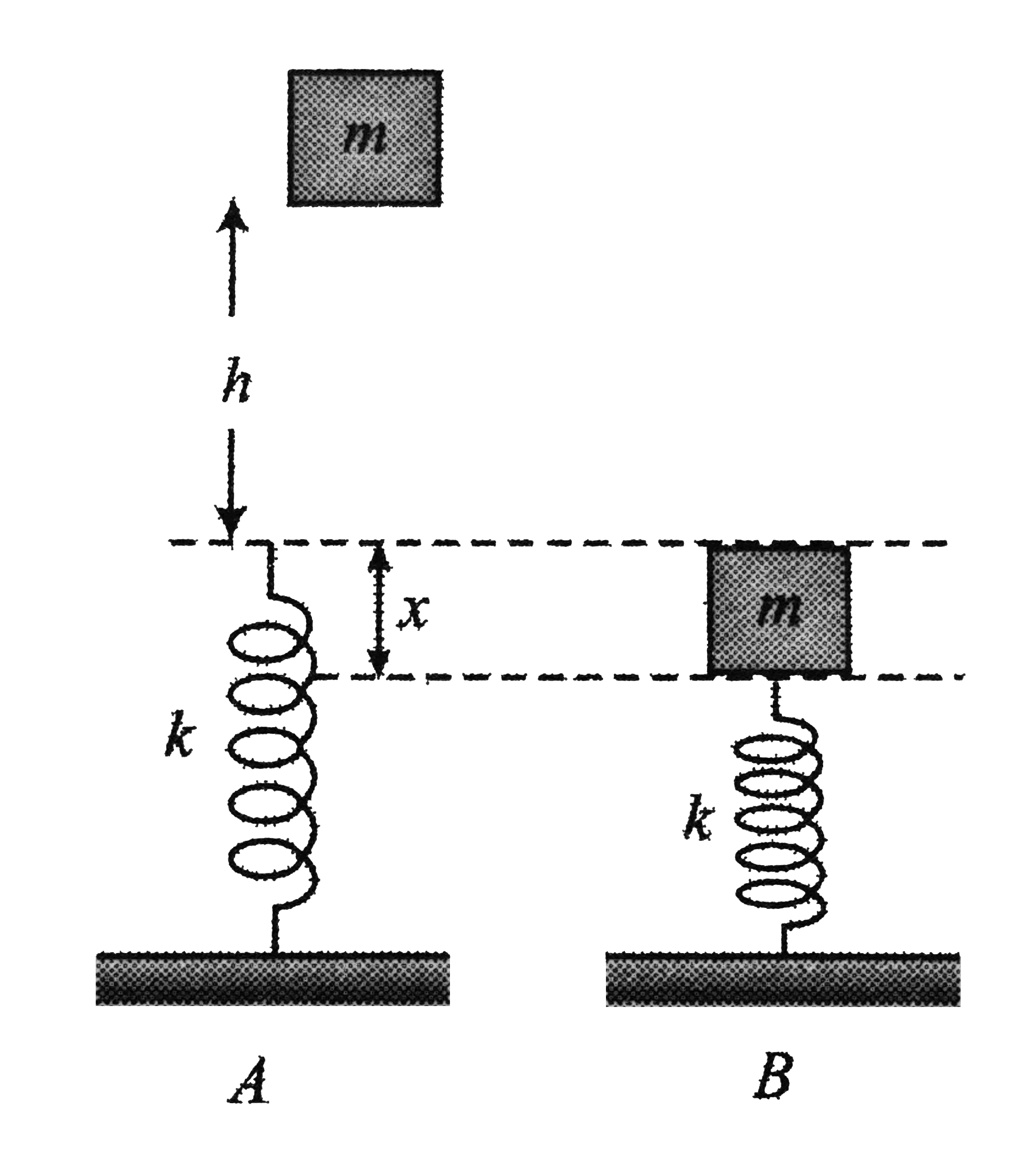
View SolutionFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.

View SolutionThe spring is compressed by a distance a and released. The block again comes to rest when the spring is elongated by a distance b. During this
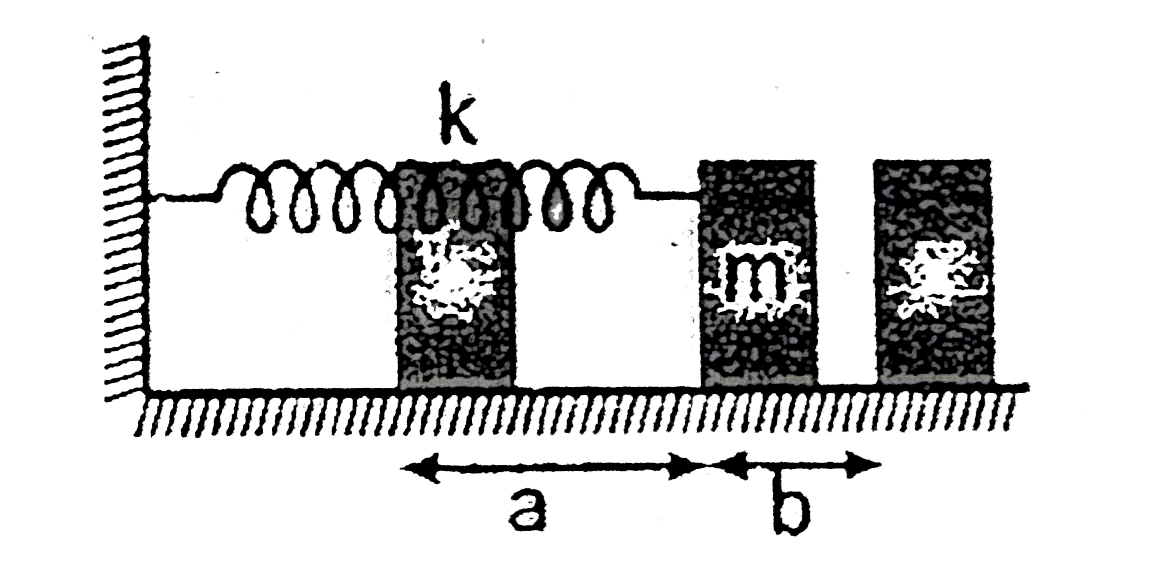
View SolutionA ball is placed on a compressed spring. When the spring is released, the ball is observed to fly away.

Why does the ball fly away?
View SolutionConsider the situation shown in figure. Initially the spring is unstretched when the system is released from rest. Assuming no friction in the puley, find the maximum eleongation of the spring.
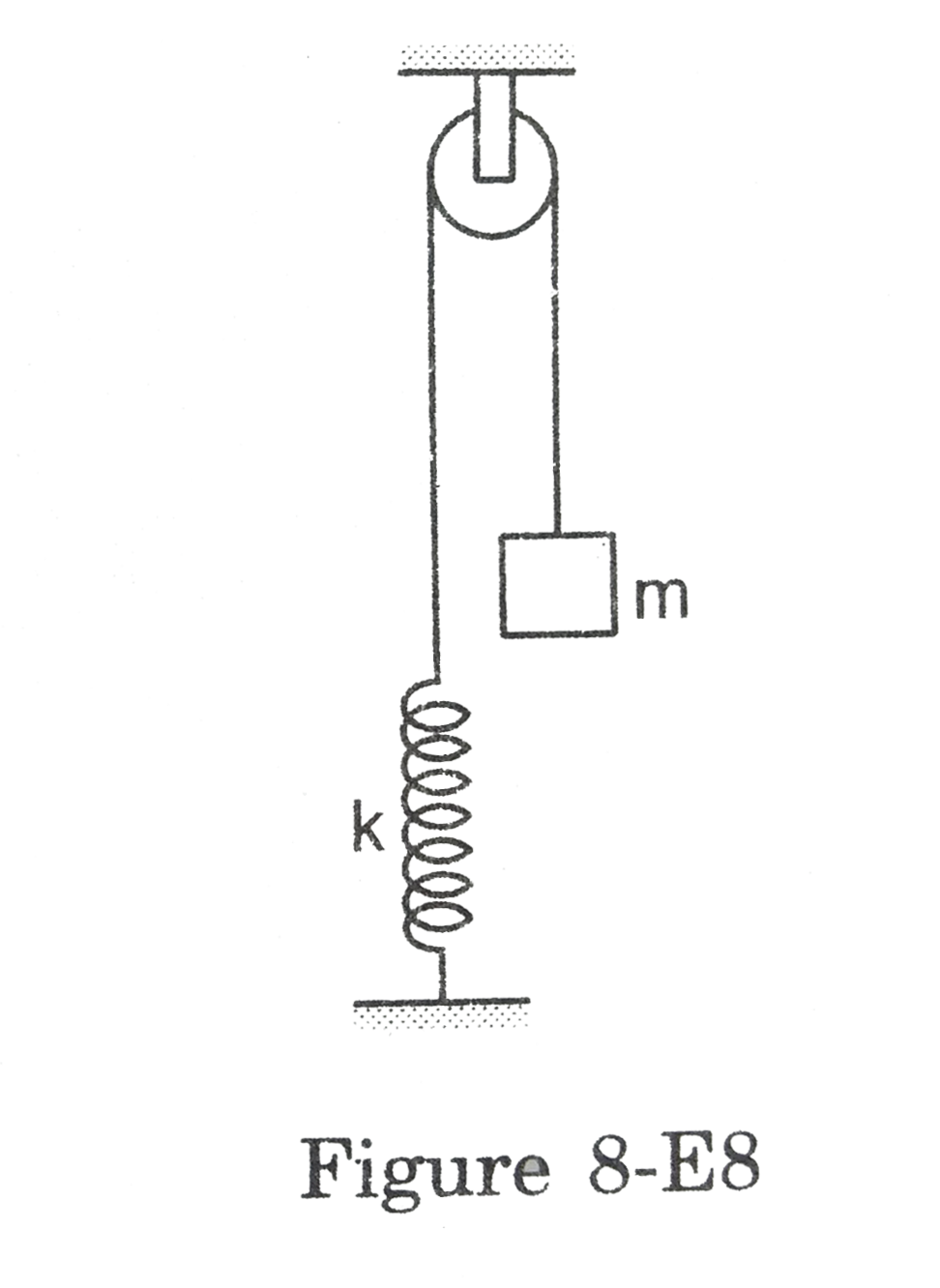
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionA block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)

View Solution
