 .
.
In the figure shown, AB=BC=2m. Friction coefficient everywhere is μ=0.2. Find the maximum compression of the spring.
The correct Answer is:B, D
Let x be the maximum extension.
 .
.
h=(2+x)sin30∘=(1+0.5x)m
The block has travelled d1=2m on rough horizontal ground and d2=(2+x)m on rough inclined ground . In the initial position block has only kinetic enetgy and in the final position spring and gravitational potential energy. so, applying the equation.
Ei−Ef= work done against friction
⇒(12mv2)−(12kx2+mgh)=μmgd1+(μmgcosθ)d2
⇒12×2×(10)2−12×x2−2×10×(1+0.5x)=0.2×2×10×2+(0.2×2×10×cos30∘)(2+x)
Solving this equation we get,
x=2.45m.
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - TYPE2
1 Video
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Miscellaneous Example
6 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
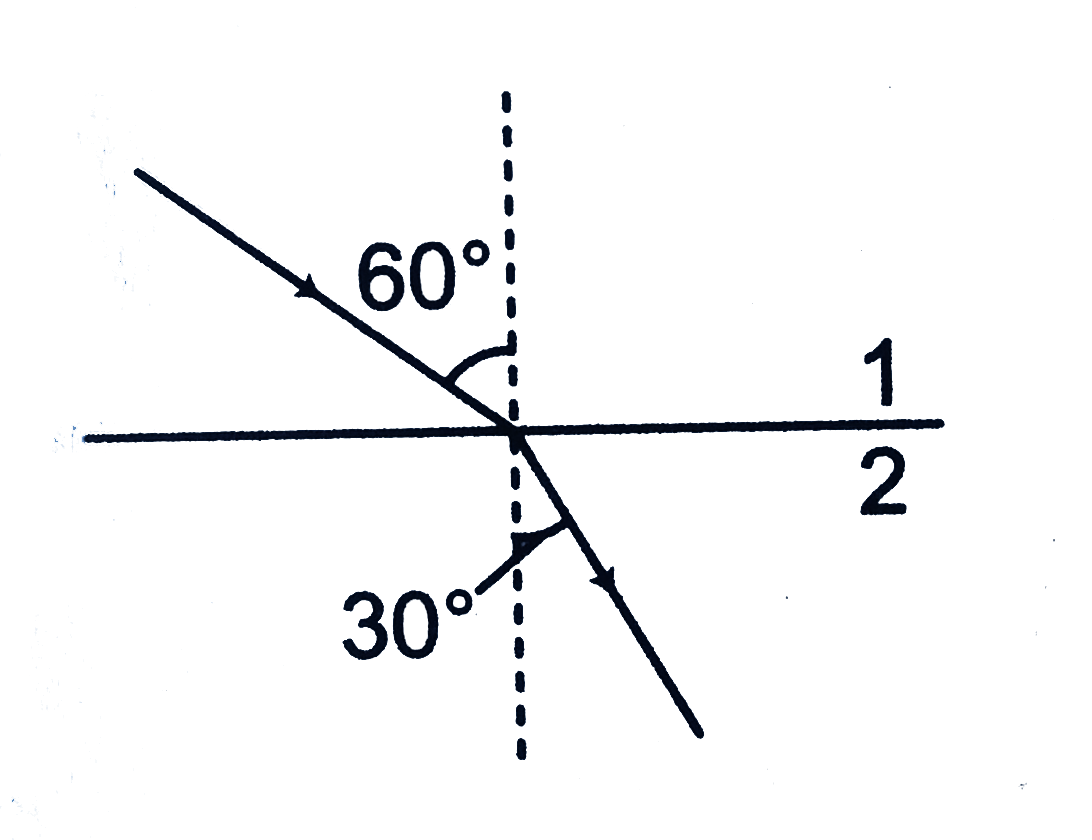
In the figure shown, find .1μ2.
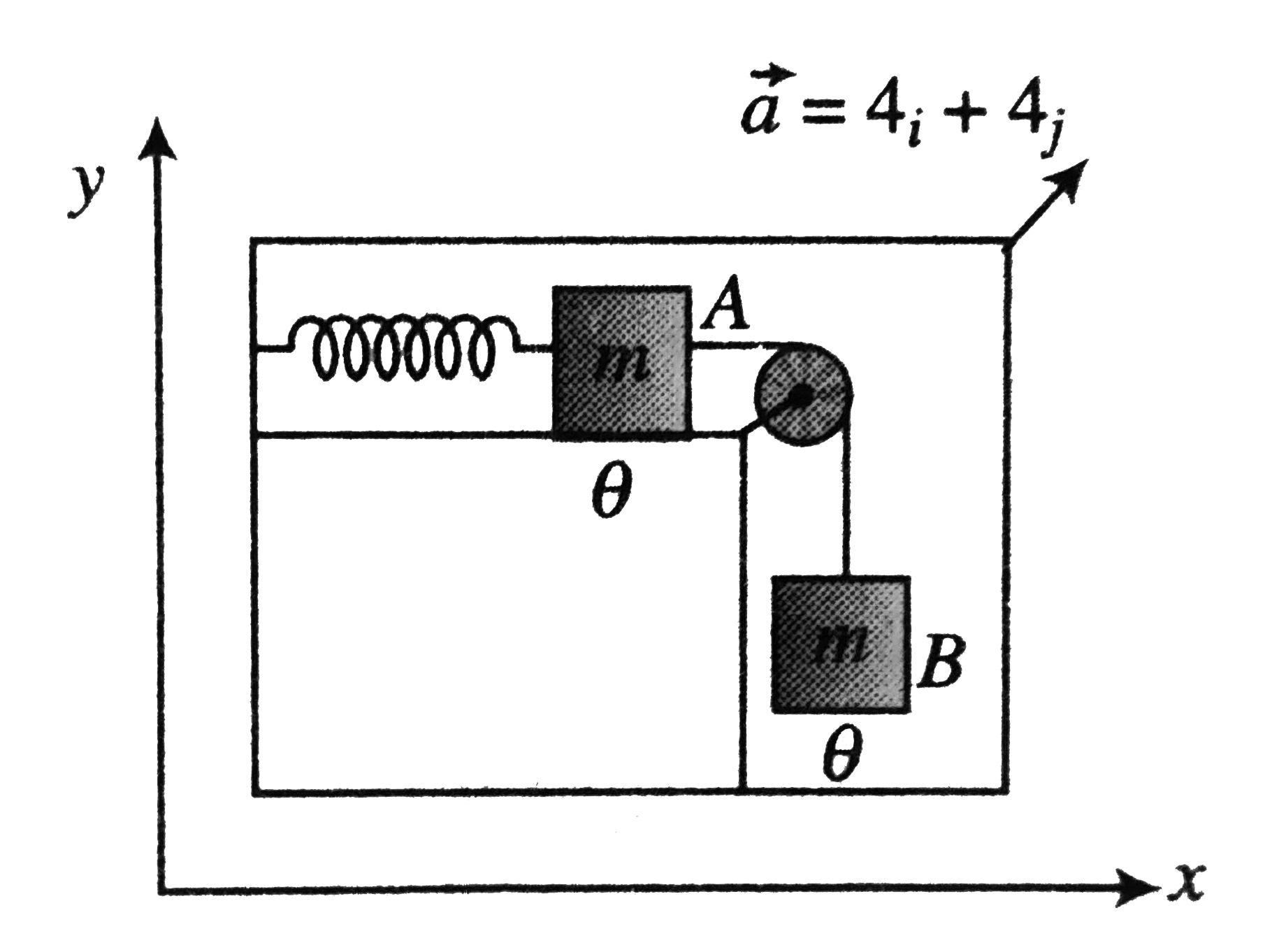
View SolutionThe arrangement shown in figure is at rest. An ideal spring of natural length l0 having spring constant k=220Nm−1, is connected to block A. Blocks A and B are connected by an ideal string passing through a friction less pulley. The mass of each block A and B is equal to m=2kg when the spring was in natural length, the whole system is given an acceleration →a as shown. If coefficient of friction of both surfaces is μ=0.25, then find the maximum extension in 10(m) of the spring. (g=10ms−2).
View SolutionFor the arrangement shown in figure, the spring is initially compressed by 3cm. When the spring is released the block collides with the wall and rebounds to compress the spring again.

(a) If the coefficient of restitution is 1√2 , find the maximum compression in the spring after collision.
(b) If the time starts at the instant when spring is released, find the minimum time after which the block becomes stationary.
View SolutionThere are two block as shown in the figure of masses 1kg and 4kg. Friction coefficient between any two surfaces are 0.2 then find maximum value of horizontal force F so that both blocks moves together.
_2019_CBT6_E01_036_Q01.png)
View SolutionA block of mass 2.0 kg is moving on a frictionless horizontal surface with a velocity of 1.0 m/s figure towards another block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100 N/m. Find the maximum compression of the spring.

View SolutionEach of the blocks shown in figure has mass 1 kg. The rear block moves with a speed of 2 m/s towards the front block kept at rest. The spring attached to the front block islight and has a spring constant 50 N/m. find the maximum compression of the spring.

View SolutionConsider Example 8, taking the coefficient of friction, μ, to be 0.5 and calculate the maximm compression of the spring.
View SolutionTwo identical blocks each of mass M=9kg are placed on a rough horizontal surface of frictional coefficient μ=0.1. The two blocks are joined by a light spring and block B is in contact with a vertical fixed wall as shown in figure. A bullet of mass m=1kg and v0=10m/s hits block A and gets embedded in it. Find the maximum compression of spring. (Spring constant =240N/m,g=10m/s2)

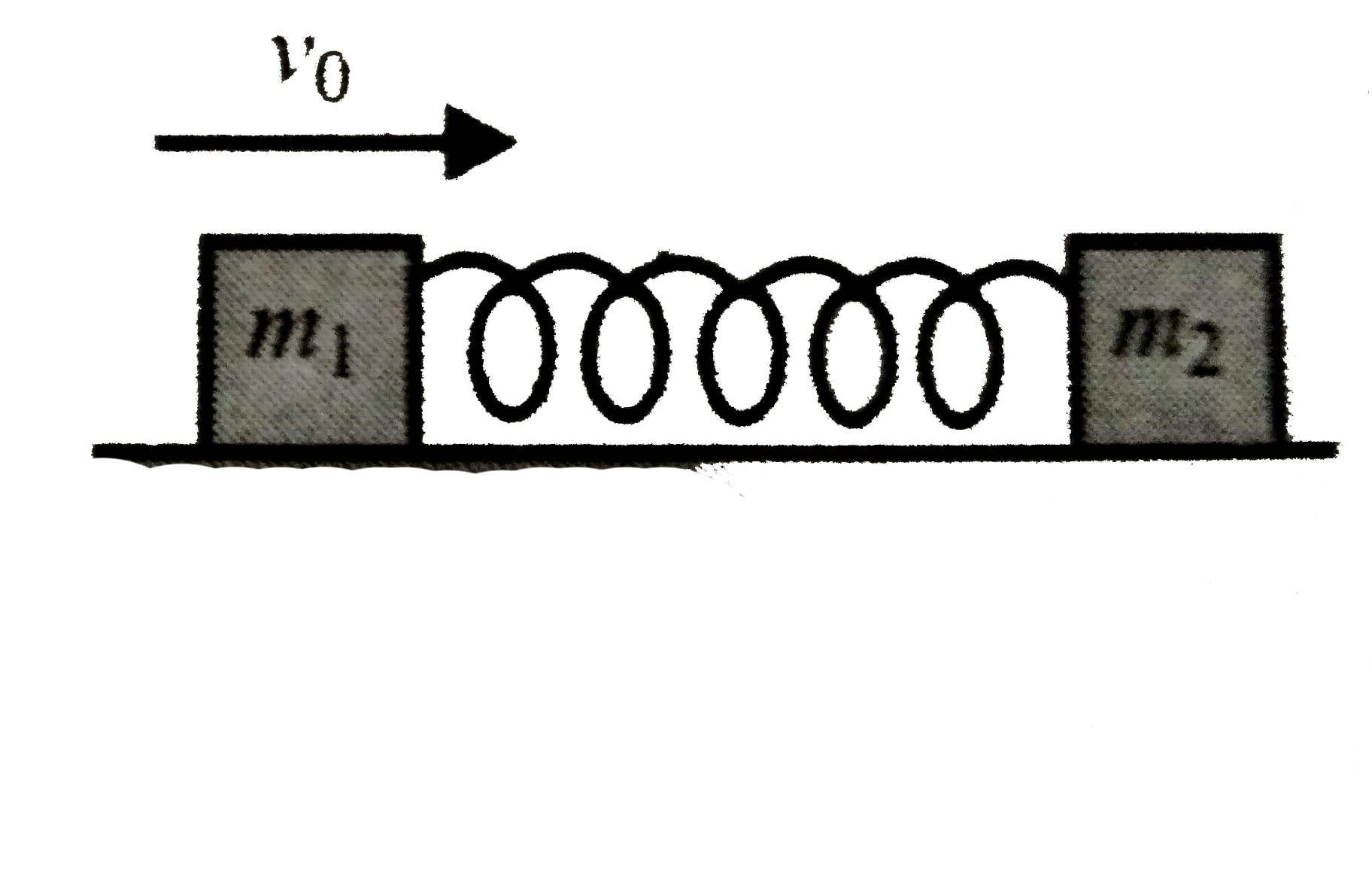
View SolutionTwo smooth blocks of mases m1andm2 attached with an ideal spring of stiffness k and kept on hrozontal surface. If m1 is projected with a horizontal velocity v0. Find the maximum compression of the spring.
View SolutionA block of mass m sliding n a smooth horizontal surface with velocity →v meets a long horizontal spring fixed ast one end and having spring constant k as shown n figure. Find the maximum compression of the spring. Will the velocity of the block be the same as v whenit comes back to the original position shown?

View Solution
