One end of a light spring of natural length d and spring constant k is fixed on a rigid wall and the other is attached to a smooth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the wall. Initially the spring makes an angle of 37∘ with the horizontal as shown in fig. When the system is released from rest, find the speed of the ring when the spring becomes horizontal.
[ sin 37∘ = 3/5]
![One end of a light spring of natural length d and spring constant k is fixed on a rigid wall and the other is attached to a smooth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the wall. Initially the spring makes an angle of 37^(@) with the horizontal as shown in fig. When the system is released from rest, find the speed of the ring when the spring becomes horizontal. [ sin 37^(@) = 3/5]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/MOT_CON_JEE_PHY_C08_SLV_016_Q01.png)
The correct Answer is:A, B, C, D
If l is the stretched length of the spring, then figure
dl=cos37∘=45, i.e. l=54d
So, the stretch x=l−d=54d−d=d4
and h=l sin 37∘=54d×35=34d
Now, taking point B as reference level and applying law of conservation of mechanical energy between A and B,
EA=EB
or mgh+12kx2=12mv∘ , [At B,h=0andx=0]
or 34mgd+12k(d4)2=12mv2 [as for A,h=34d and y=14d]
or v=d√3g2d+k16m)
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - TYPE2
1 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Miscellaneous Example
6 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
On end of a light spring of natural length d and spring constant k is fixed on a rigid wall and the other is attached to a smooth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the wall. Initially the spring makes an angle of 37∘ with the horizontal. as shown in figure. When the system is released from rest, find the speed of the ring when the spring becomes horizontal. (sin37∘=35).

View SolutionOne end of a light spring of natural length 4m and spring constant 170 N/m is fixed on a rigid wall and the other is fixed to a smooth ring of mass 12 kg which can slide without friction in a verical rod fixed at a distance 4 m from the wall. Initially the spring makes an angle of 37∘ with the horizontal as shown in figure. When the system is released from rest, find the speed of the ring when the spring becomes horizontal.
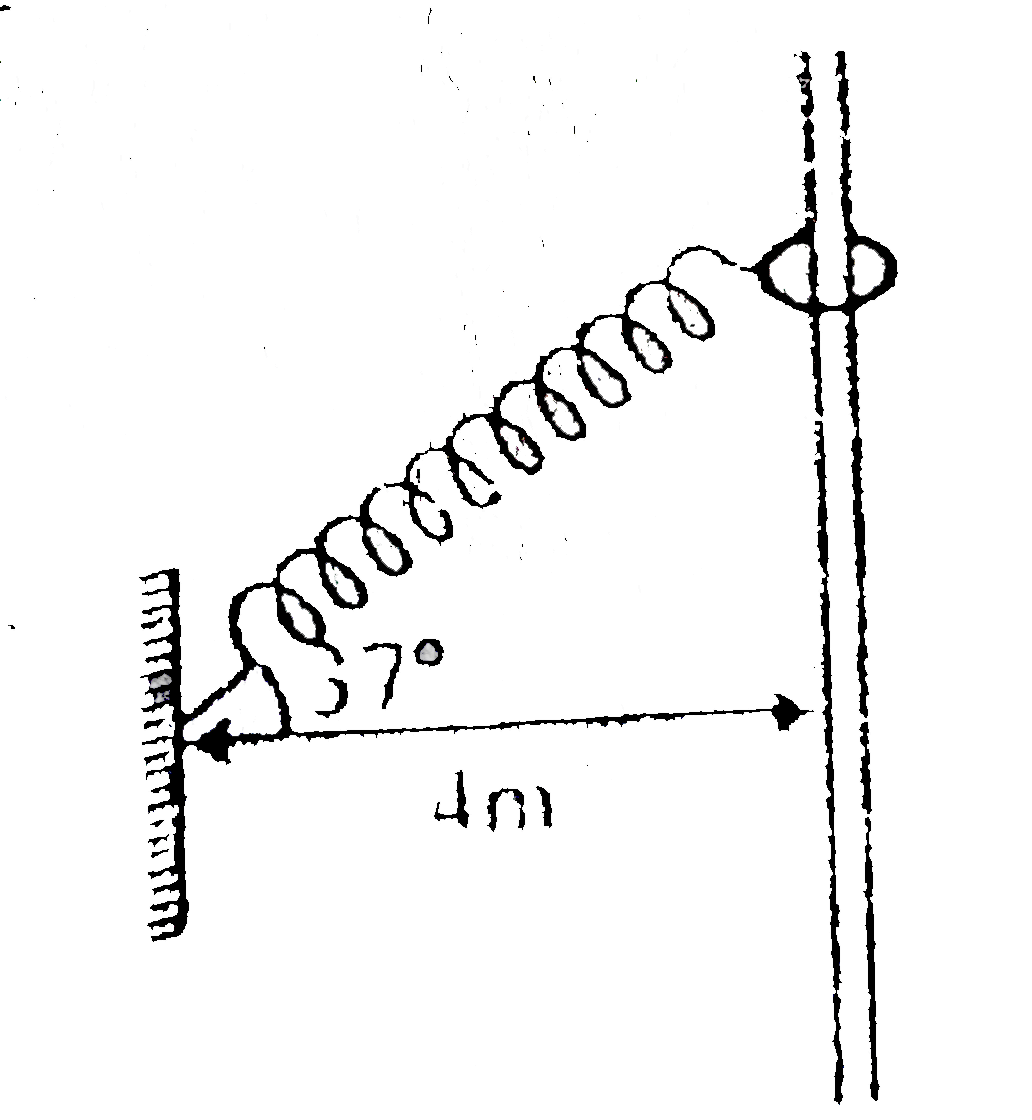
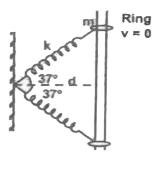
View SolutionOne end a light spring of natural length d and spring constant k(=mg/d) is fixed on a rigid support and the other end is fixed to a smoth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the support. Initially , the spring makes an angle of 37∘ with the horizontal as shown in the figure. The system is released from rest. The speed of the ring at the same angle subtended downward will be
View Solutionone end of a spring of natural length ha and spring constant k is fixed at the ground and the other is fitted with a smooth ring of mass m which is allowed to slide on a horizontal rod fixed at a height h figure. Initially, the spring makes an angle of 370 with the vertical when the system is released from rest. find the speed of the ring when the spring becomes vertical.

View SolutionOne end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacement, the work by the spring is 12kx2. The possible cases are
View SolutionOne end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacment, the work done by the spring is +(12)kx2. The possible cases are.
View SolutionOne end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacement, the work done by the spring is +(12)kx2. The possible cases are.
View SolutionOne end of a spring of force constant k is fixed to a vertical wall and the other to a blcok of mass m resting on a smooth horizontal surface. There is another wall at distance x0 from the block. The spring is then compressed by 2x0 and released. The time taken to strike the wall is

View SolutionOne end of a spring of force constant k is fixed to a vertical wall and the other to a blcok of mass m resting on a smooth horizontal surface. There is another wall at distance x0 from the block. The spring is then compressed by 2x0 and released. The time taken to strike the wall is

View SolutionA ring of mass m=10kg can slide through a vertical rod with friction. It is connected with a spring of force constant k=100Nm−1. The relaxed length of spring is 4m. The ring is displaced 3m as shown in the figure and released. Find velocity of ring when spring becomes horizontal.
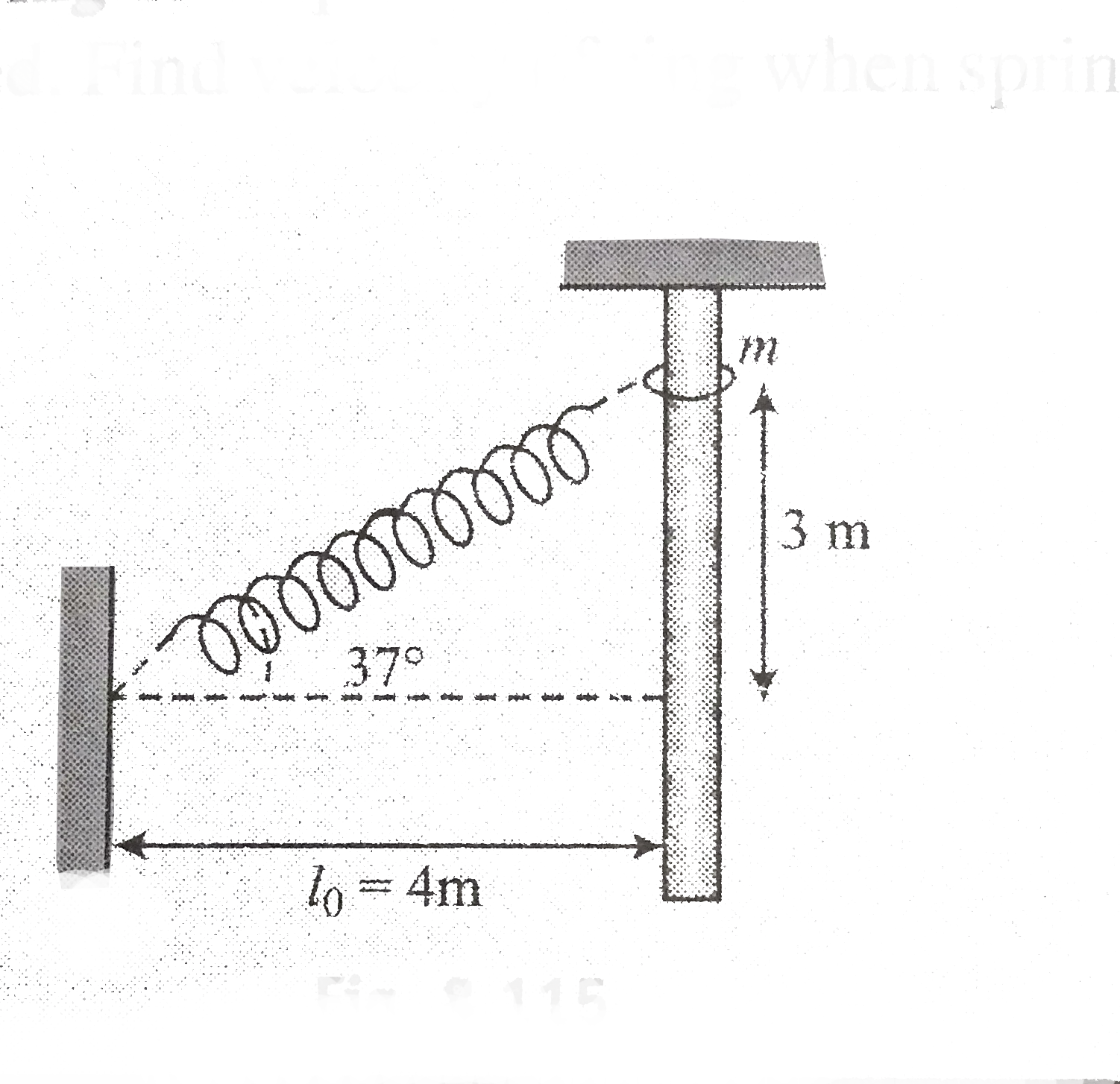
View Solution
