A force F=−k(^ˆi+xˆj) (where k is a positive constant) acts on a particle moving in the x−y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0) and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
(a) −2ka2 , (b) 2ka2,(c)-ka^(2),(d)ka^(2)
The correct Answer is:A, B, C
To solve the problem, we need to calculate the total work done by the force F=−k(^i+x^j) on a particle moving in the x−y plane from the origin to the point (a,0) and then to the point (a,a).
Step 1: Define the Work Done
The work done by a force F when moving along a path is given by the integral:
W=∫F⋅dr
where dr is the differential displacement vector.
Step 2: Set Up the Displacement Vector
In the x−y plane, the displacement vector can be expressed as:
dr=dx^i+dy^j
Step 3: Express the Force Vector
The force vector is given as:
F=−k(0^i+x^j)=−k(0^i+y^j)
Step 4: Calculate Work Done Along Path OA (from O to A)
1. From the origin O(0,0) to point A(a,0), the movement is along the x-axis, where y=0.
2. Therefore, dy=0 and y=0 during this segment.
The work done along OA is:
WOA=∫a0F⋅dr=∫a0(−k(0^i+0^j))⋅(dx^i+0^j)=∫a00dx=0
Step 5: Calculate Work Done Along Path AB (from A to B)
1. From point A(a,0) to point B(a,a), the movement is along the y-axis, where x=a is constant.
2. Therefore, dx=0 and x=a during this segment.
The work done along AB is:
WAB=∫a0F⋅dr=∫a0(−k(0^i+a^j))⋅(0^i+dy^j)=∫a0−kady=−ka∫a0dy=−ka2
Step 6: Total Work Done
The total work done W is the sum of the work done along both segments:
W=WOA+WAB=0+(−ka2)=−ka2
Conclusion
The total work done by the force F on the particle is:
−ka2
The work done by a force F when moving along a path is given by the integral:
W=∫F⋅dr
where dr is the differential displacement vector.
In the x−y plane, the displacement vector can be expressed as:
dr=dx^i+dy^j
The force vector is given as:
F=−k(0^i+x^j)=−k(0^i+y^j)
1. From the origin O(0,0) to point A(a,0), the movement is along the x-axis, where y=0.
2. Therefore, dy=0 and y=0 during this segment.
WOA=∫a0F⋅dr=∫a0(−k(0^i+0^j))⋅(dx^i+0^j)=∫a00dx=0
1. From point A(a,0) to point B(a,a), the movement is along the y-axis, where x=a is constant.
2. Therefore, dx=0 and x=a during this segment.
WAB=∫a0F⋅dr=∫a0(−k(0^i+a^j))⋅(0^i+dy^j)=∫a0−kady=−ka∫a0dy=−ka2
The total work done W is the sum of the work done along both segments:
W=WOA+WAB=0+(−ka2)=−ka2
The total work done by the force F on the particle is:
−ka2
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - TYPE2
1 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Miscellaneous Example
6 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
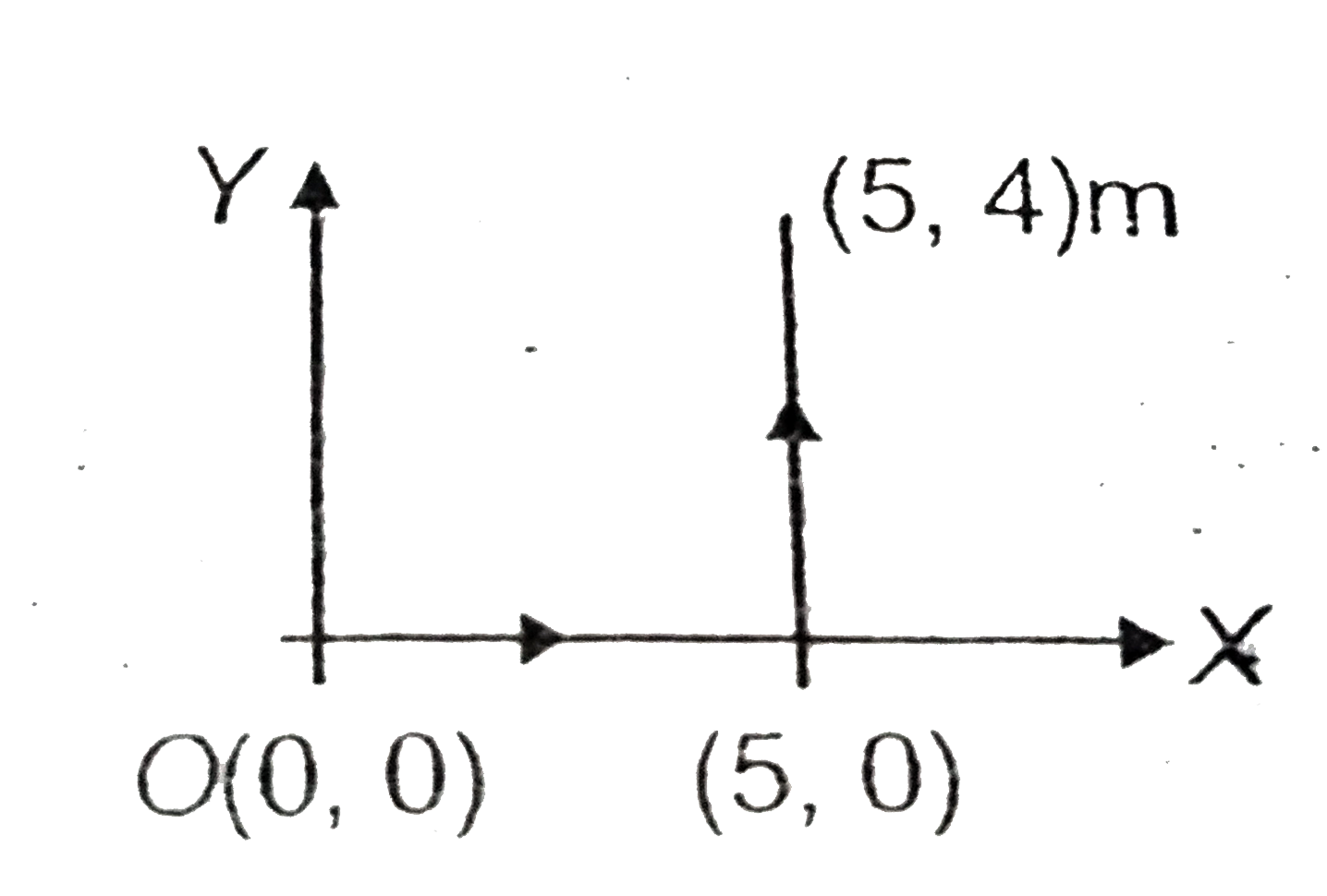
A force →F=(4ˆi+5ˆj)N acts on a particle moving in XY plane. Starting from origin, the particle first goes along x-axis to the point (5.0) m and then parallel to the Y-axis to the point (5,4 m. The total work done by the force on the particle is
View SolutionA particle moves along the x-axis from x=0 to x=5m under the influence of a given by F=7−2x+3x2. The work done by the applied force to the particle is.
View Solution
Knowledge Check
A force F is related to the position of a particle by the relation F=(10x2)N . Find the work done by the force when the particle moves from x=2m→x=4m.
A563 JB560 JC5603 JD3560 J
A uniform force of (3ˆi+ˆj) N acts on a particle of mass 2kg. Hence, the particle is displaced from position (2ˆi+ˆk)m to position (4ˆi+3ˆj−ˆk)m. The work done by the force on the particle is
View SolutionA particle is moving along the x-axis and force acting on it is given by F=F0sinωxN, where ω is a constant. The work done by the force from x=0 to x=2 will be
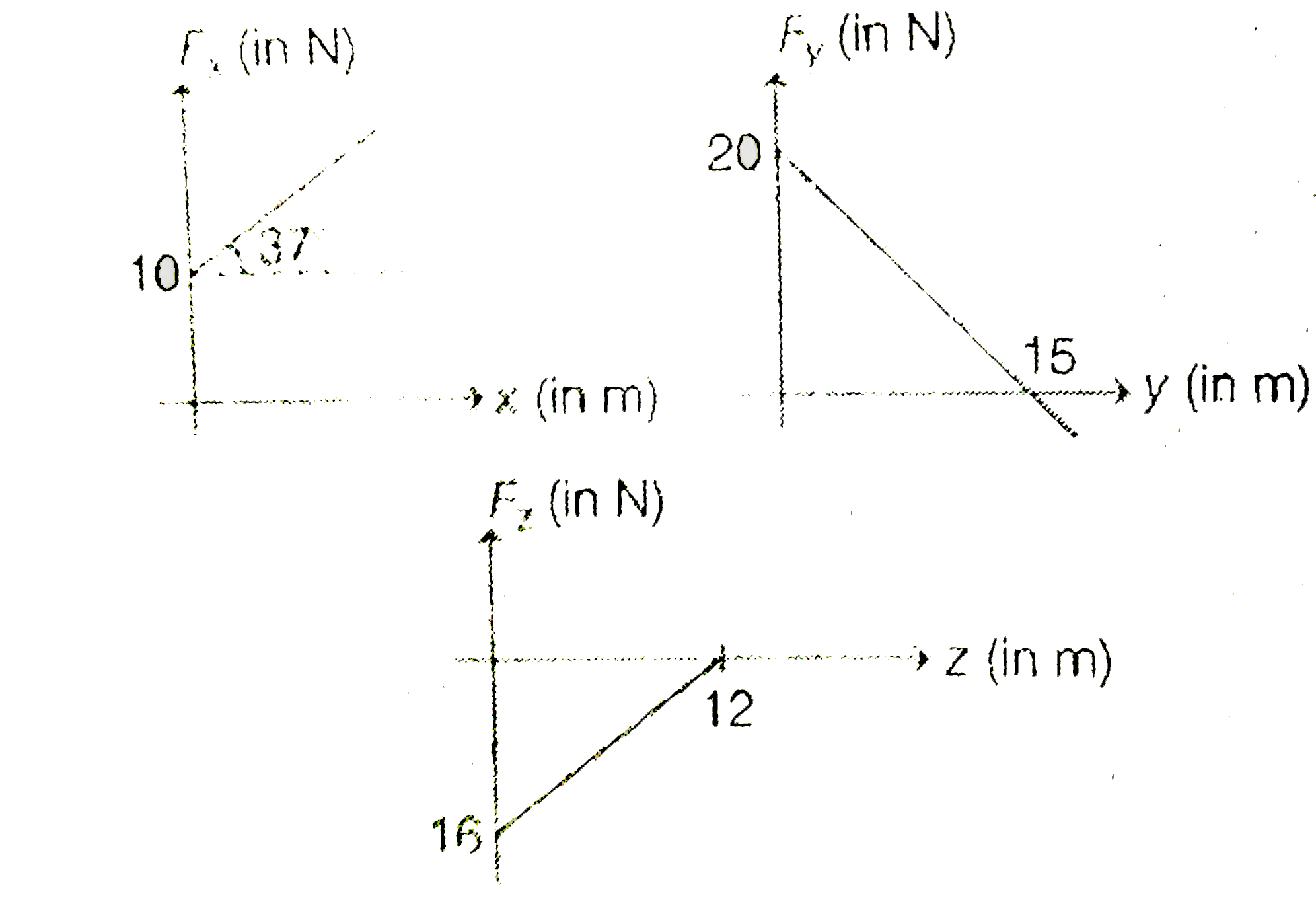
View SolutionThree components of a force acting on a particle are varying according to the graphs as shown. To reach at point B(8, 20, 0)m from point A(0, 5, 12)m the particle moves on paths parallel to x-axis then y-axis and then z-axis, then work done by this force is:
View SolutionA particle of mass m initially moving with speed v.A force acts on the particle f=kx where x is the distance travelled by the particle and k is constant. Find the speed of the particle when the work done by the force equals W.
View SolutionA force bar F = (3hat i-4 hat j +b hat k)N is acting on the particle which is moving from point A ( 0-1, 1) m to the point B(2, 2 3) m If net work done by the force on the particle is zero then value of b is
View SolutionA force F=−kx3 is acting on a block moving along x-axis. Here, k is a positive constant. Work done by this force is
View SolutionA particle of mass m initially at rest. A variabl force acts on the particle f=kx2 where k is a constant and x is the displacment. Find the work done by the force f when the speed of particles is v.
View Solution
