A small mass m starts from rest and slides down the smooth spherical surface of F. Assume zero potential energy at the top. Find
(a) the change in potential energy,
(b) the kinetic energy,
(c) the speed ot the mass as a function of the angle θ made by the radius through the mass with the vertical.
The correct Answer is:A, C
To solve the problem step by step, we will analyze the situation of a mass sliding down a smooth spherical surface.
Step 1: Understanding the Setup
- We have a small mass m that starts from rest at the top of a smooth spherical surface of radius R.
- The potential energy is considered zero at the top of the sphere.
- As the mass slides down, it descends a height h which can be expressed in terms of the angle θ made with the vertical.
Step 2: Finding the Change in Potential Energy
- At the top of the sphere, the height h is R (the radius).
- When the mass descends to an angle θ, the height h can be expressed as:
h=R−Rcosθ=R(1−cosθ)
- The change in potential energy ΔU as the mass descends is given by:
ΔU=−mgh
Substituting for h:
ΔU=−mg(R(1−cosθ))=−mgR(1−cosθ)
Step 3: Finding the Kinetic Energy
- The change in kinetic energy ΔK is equal to the change in potential energy (due to conservation of mechanical energy):
ΔK=−ΔU=mgR(1−cosθ)
Step 4: Relating Kinetic Energy to Speed
- The kinetic energy can also be expressed as:
K=12mv2
- Setting the two expressions for kinetic energy equal gives:
12mv2=mgR(1−cosθ)
- We can cancel m from both sides (assuming m≠0):
12v2=gR(1−cosθ)
- Solving for v2:
v2=2gR(1−cosθ)
- Taking the square root to find v:
v=√2gR(1−cosθ)
Final Answers
(a) The change in potential energy:
ΔU=−mgR(1−cosθ)
(b) The kinetic energy:
K=mgR(1−cosθ)
(c) The speed of the mass as a function of the angle θ:
v=√2gR(1−cosθ)
- We have a small mass m that starts from rest at the top of a smooth spherical surface of radius R.
- The potential energy is considered zero at the top of the sphere.
- As the mass slides down, it descends a height h which can be expressed in terms of the angle θ made with the vertical.
- At the top of the sphere, the height h is R (the radius).
- When the mass descends to an angle θ, the height h can be expressed as:
h=R−Rcosθ=R(1−cosθ)
- The change in potential energy ΔU as the mass descends is given by:
ΔU=−mgh
Substituting for h:
ΔU=−mg(R(1−cosθ))=−mgR(1−cosθ)
- The change in kinetic energy ΔK is equal to the change in potential energy (due to conservation of mechanical energy):
ΔK=−ΔU=mgR(1−cosθ)
- The kinetic energy can also be expressed as:
K=12mv2
- Setting the two expressions for kinetic energy equal gives:
12mv2=mgR(1−cosθ)
- We can cancel m from both sides (assuming m≠0):
12v2=gR(1−cosθ)
- Solving for v2:
v2=2gR(1−cosθ)
- Taking the square root to find v:
v=√2gR(1−cosθ)
(a) The change in potential energy:
ΔU=−mgR(1−cosθ)
K=mgR(1−cosθ)
v=√2gR(1−cosθ)
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Exercise 9.1
10 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Exercise 9.2
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - TYPE2
1 Video
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
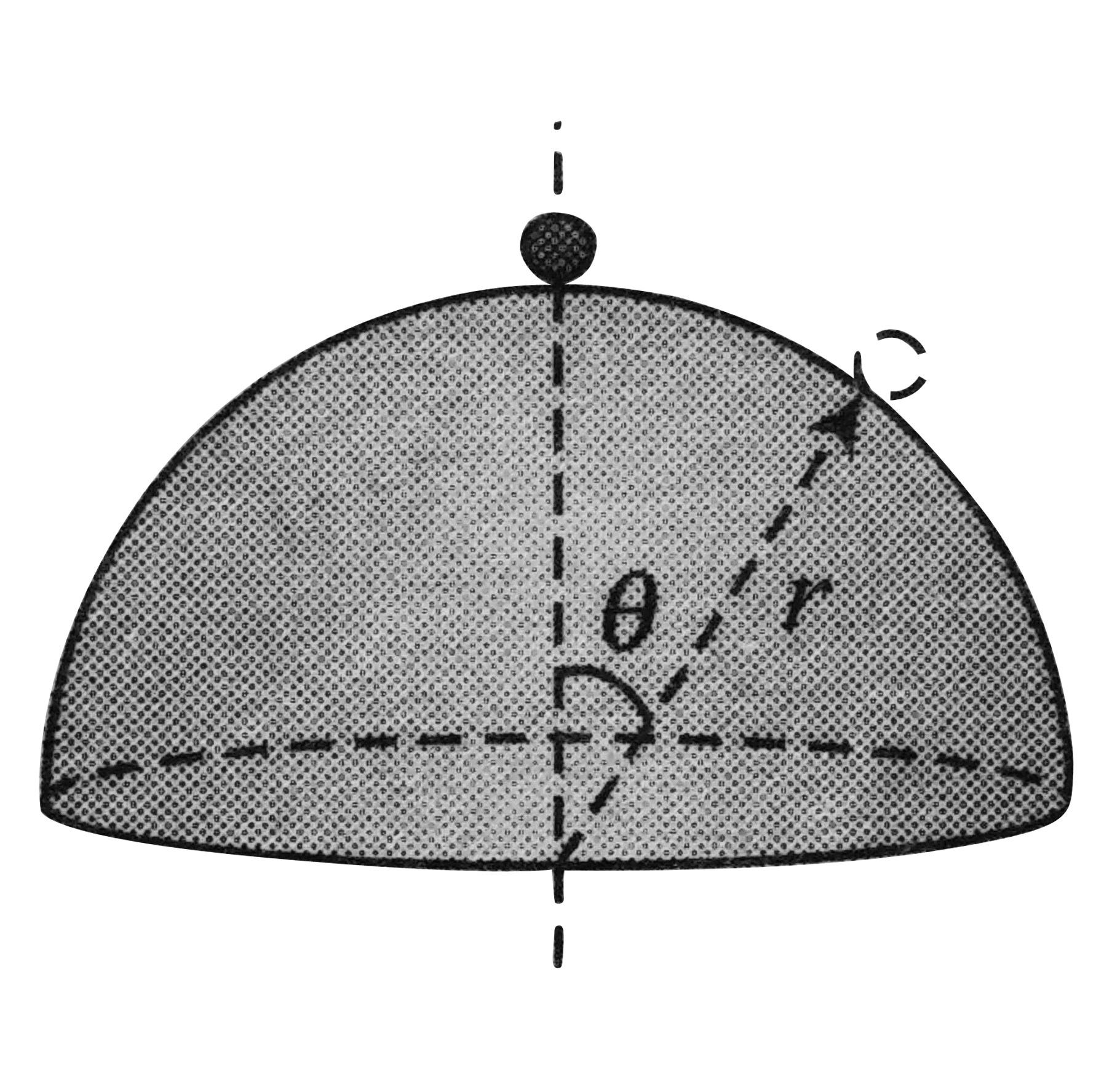
A point mass m starts from rest and slides down the surface of a frictionless hemisphere of radius r as shown figure. Measure angle from the vertical and potential energy from the top. Find
a. Find the changes in potential energy of the mass with angle
b. Find the kinetic energy as a function of angle
c. Find the radial and tangential acceleration as a function of angle
d. Find the angle at which the mass files off the hemisphere
e. If there is friction between the mass and hemisphere, does the mass fly off at a greater or lesser angle than in part (d) ?
View SolutionA small mass m starts from rest and slides down the surface of a frictionless solid sphere of radius R. Calculate the angle at which the mass flies off the sphere. If there is friction between the mass and the sphere, does the mass of fly off at a greater or lesser angle than the previous one ?
View Solution
Knowledge Check
The change in the gravitational potential energy when a body of a mass m is raised to a height nR above the surface of the earth is (here R is the radius of the earth)
AmgREn(n−1)BmgRECmgREn(n+1)DmgREn
Find the change in the gravitational potential energy when a body of mass m is raised to a height nR above the surface of the earth. (Here, R is the radius of the earth)
View SolutionA body of mass m is lifted up from the surface of earth to a height three times the radius of the earth R. The change in potential energy of the body is
View SolutionA mass is taken from surface to a height h. The change in potential energy in this process is equal to the change in potential energy if it is now taken from that point to infinity. What is the value of h?
View SolutionA particle of mass m starts to slide down from the top of the fixed smooth sphere. What is the tangential acceleration when it break off the sphere ?
View SolutionWhat is the change is potential energy (in calories) of a 10 kg mass after 41.8m fall?
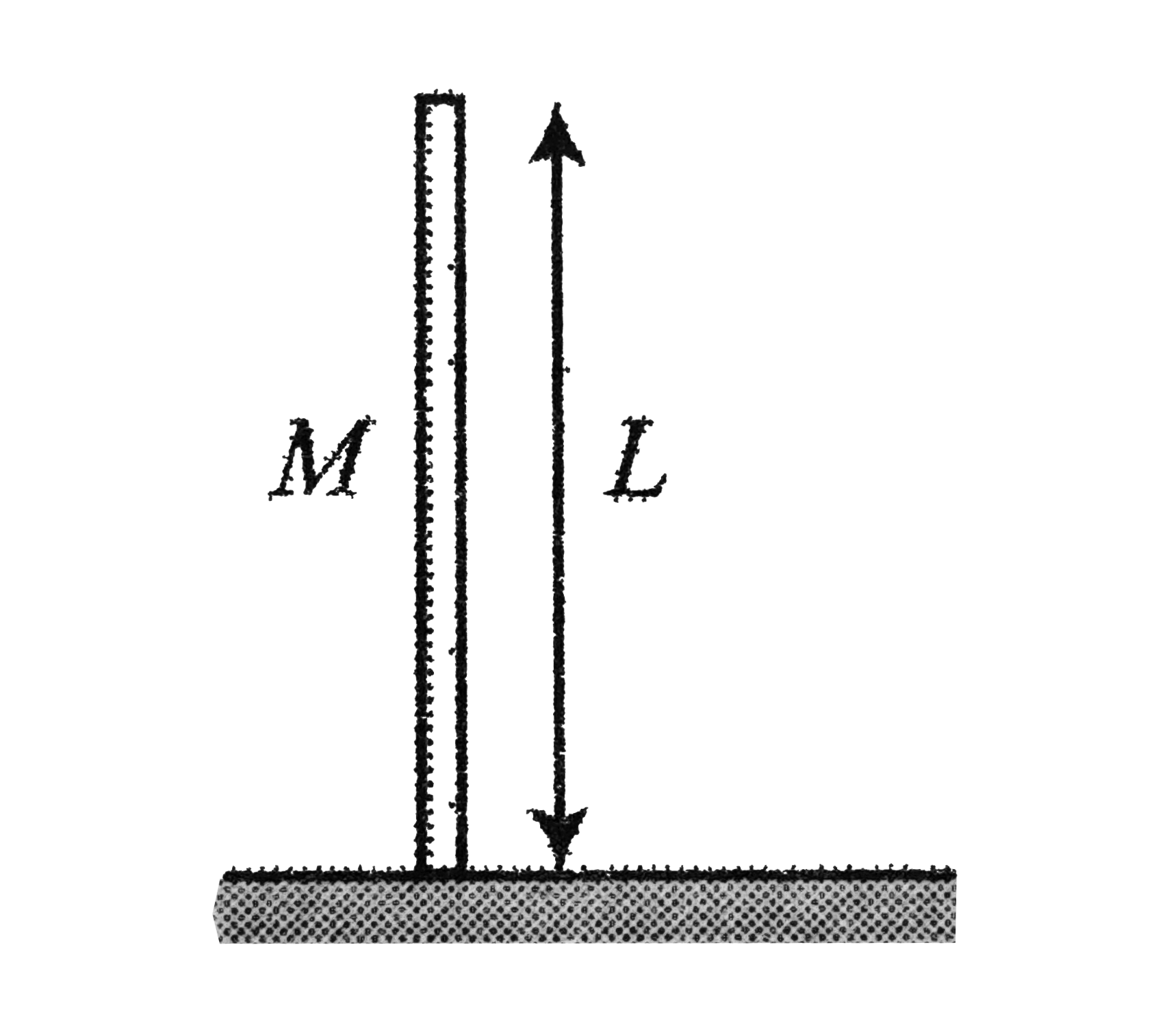
View SolutionA uniform rod of mass M and length L is held vertically upright on a horizontal surface as shown in figure. Assuming zero potential energy at the base of the rod, determine the potential energy of the rod.
View SolutionDefine potential energy. Derive an expression for the potential energy of a body of mass m, at a height h above the surface of the Earth.
View Solution
