A small disc of mass m slides down a smooth hill of height h without initial velocity and gets onto a plank of mass M lying on the horizontal plane at the base of the hill. (figure). Due to friction between the disc and the plank the disc slows down and, beginning with a certain moment, moves in one piece with the plank.
(1) Find the total work performed by the friction forces in this process.
(2) Can it be stated that the result of obtained does not depend on the choice of the reference frame?
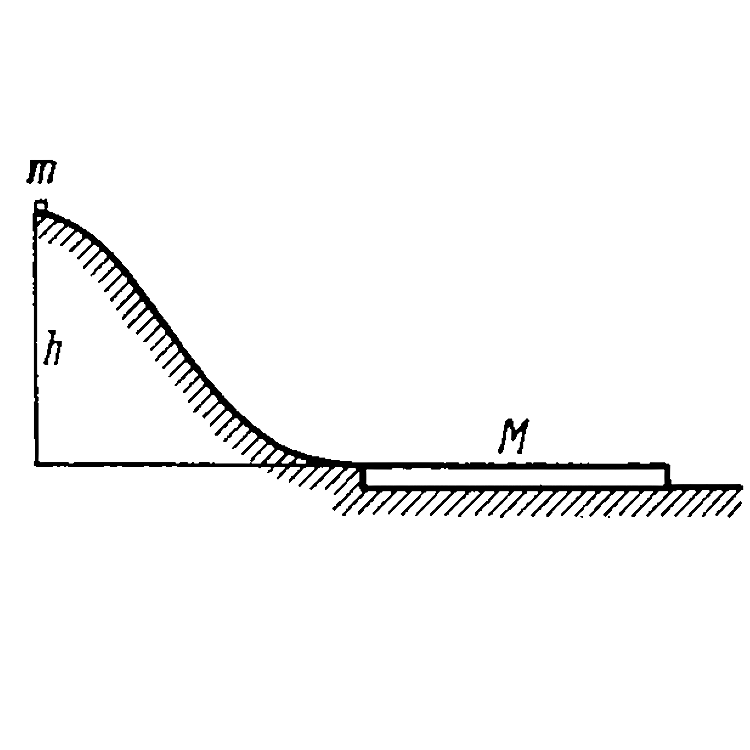
(a) whan the disc slides down and comes onto the plank, then
mgh=12mv2
∴v=√(2gh)
Let v1 be the common velocity of both, the disc and plank when they move together. From law of conservation of linear momentum,
mv=(M+m)v1
∴v1=mv(M+m)
Now, change in KE=(K)f−(K)i=(work done)friction
∴12(M+m)v21−12mv2=(work done)friction
or Wfr=12(M=m)[mvM+m]2−12mv2
=12mv2[mM+m−1]
as12mv2=mgh
Wfr=−mgh[MM+m]
(b) In part (a), we have calculated work done from the ground frame of reference. Now let us take plank as the reference frame.
 .
.
Accleration of plank a0=fm=μmgM
Free body diagram of disc with respect to plank is shown in figure.
Here, ma0=pseudo force.
Retardation of disc w.r.t. plank.
ar=f+ma0m=μmg+μm2gMm=μmg+μmgM
=(M+mM)μg
The disc will stop after travalling a distance Sr relative to plank, where
Sr=v2r2arMgh(M+m)μg,(0=v2r−2arSr)
∴ Work done by friction in this frame of reference
Wfr=−fSr−(μmg)[Mgh(M+m)μg]
=−Mmgh(M+m)
which is same as part (a).
Topper's Solved these Questions
- WORK, ENERGY & POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY & POWERExercise:Exercise 9.1
Explore 10 Videos
- WORK, ENERGY & POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY & POWERExercise:Exercise 9.2
Explore 9 Videos
- WORK, ENERGY & POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY & POWERExercise:TYPE2
Explore 1 Video
- WAVE MOTIONBook:DC PANDEY ENGLISHChapter:WAVE MOTIONExercise:Integer Type Question
Explore 11 Videos
- WORK, ENERGY AND POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY AND POWERExercise:MEDICAL ENTRACES GALLERY
Explore 33 Videos
Similar Questions
A disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Force of friction between the disc and the plank is
View SolutionA block of mass m is pushed with a velocity v0 along the surface of a trolley car of mass M. If the horizontal ground is smooth and the coefficient of kinetic friction between the block of plank is μ. Find the minimum distance of relative sliding between the block and plank.

View SolutionIn the figure shown, a solid sphere of mass 'm' and radius r is released from a height 6r to slide down a smooth surface. A plank of same mass 'm' touches the horizontal portion of the surface at the ground. The co-efficient of friction between the plank and the sphere is μ and that between the plank and the ground is μ/4. Find the work done by the friction force between the plank and the ground till the sphere starts pure rolling on the plank. Neglect the height of the plank.

View SolutionA man of mass m starts moving on a plank of mass M with constant velocity v with respect to plank. If the plank lies on a smooth horizontal surface, then velocity of plank with respect to ground is
View SolutionA small disc A slides down with initial velocity equal to zero from the top of a smooth hill of height H having a horizontal portion. What must be the height of the horizontal portion h to ensure the maximum distance s covered by the disc? What is it equal to?

View SolutionA plank of mass 10 kg and a block of mass 2 kg are placed on a horizontal plane as shown in the figure. There is no friction between plane and plank. The coefficient of friction between block and plank is 0.5 .A force of 60 N is applied on plank horizontally. In first 2 s the work done by friction on the block is

View SolutionA uniform circular disc of mass m is set rolling on a smooth horizontal table with a uniform linear velocity v. Find the total K.E. of the disc.
View SolutionA block of mass m=2kg of shown dimensions is placed on a plank of mass M = 6Kg which is placed on smooth horizontal plane. The coefficient of friction between the block and the plank is μ=13. If a horizontal froce F is applied on the plank, then find the maximum value of F (in N) for which the block and the plank move together

View SolutionA force F acts tangentially at the highest point of a disc of mass m kept on a rough horizontal plane. If the disc rolls without slipping, the acceleration of centre of the disc is:

View SolutionA man of mass m moves on a plank of mass M with a constant velocity u with respect to the plank, as shown in figure.
a.If the plank rests on smooth horizontal surface, determine the velocity of the plank. .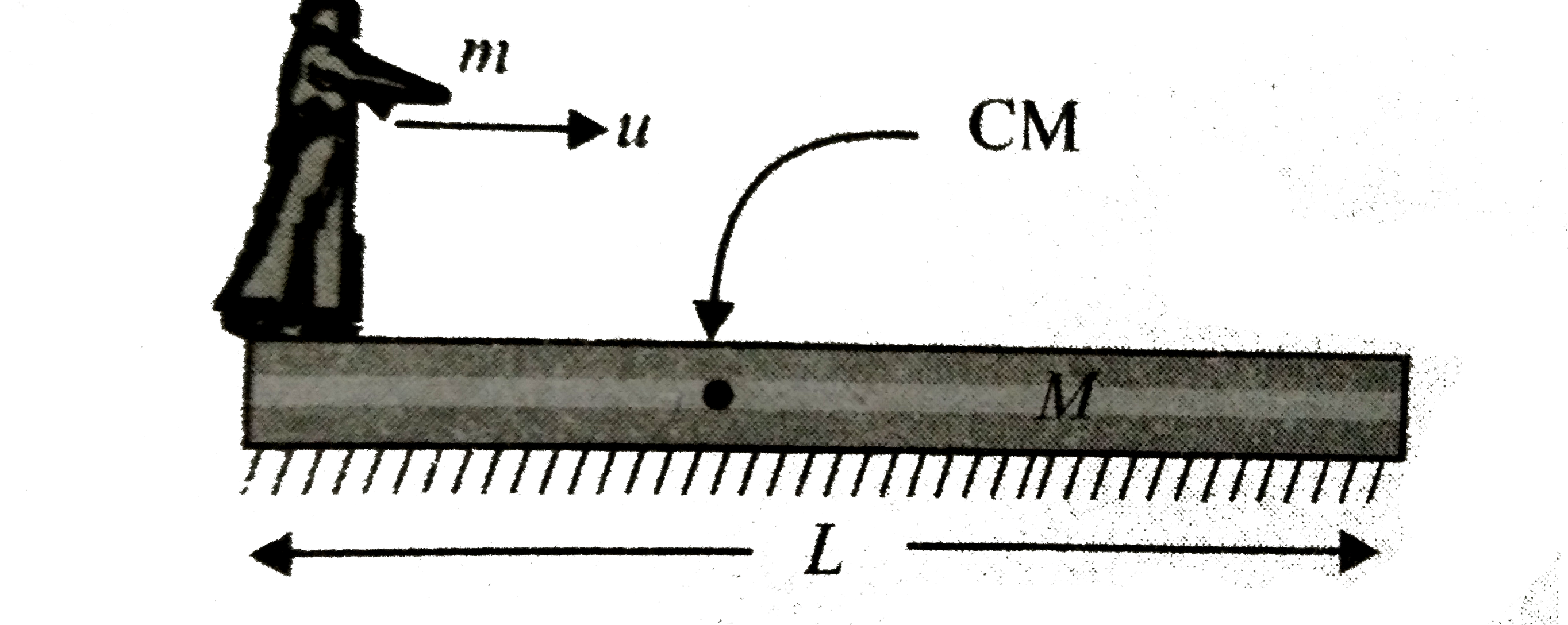
View Solution

