Question

A single conservative force F(x) acts on a on a (1.0kg ) particle that moves along the x-axis. The potential energy U(x) is given by:
$U\left(x\right)=20+{(x-2)}^2$
where, x is meters. At $x=5.0m$ the particle has a kinetic energy of $20J$
(a) What is the mechanical energy of the system?
(b) Make a plot of U(x) as a function of x for $-10m\le x\le 10m$, and on the same graph draw the line that represents the mechanical energy of the system. Use part (b) to determine.
(c) The least value of x and
(d) the greatest value of x between which the particle can move.
(e) The maximum kinetic energy of the particle and
(f) the value of x at which it occurs.
(g) Datermine the equation for $F\left(x\right)$ as a function of x.
(h) For what (finite ) value of x does $F\left(x\right)=0$?.

Answer

B::C

Explanation

(a) Potential energy at `x=5.0 m` is
`U=20 + (5-2)^(2) =29J`
`:.` Mechanical energy
`E=K + U=20 + 29=49J`
.
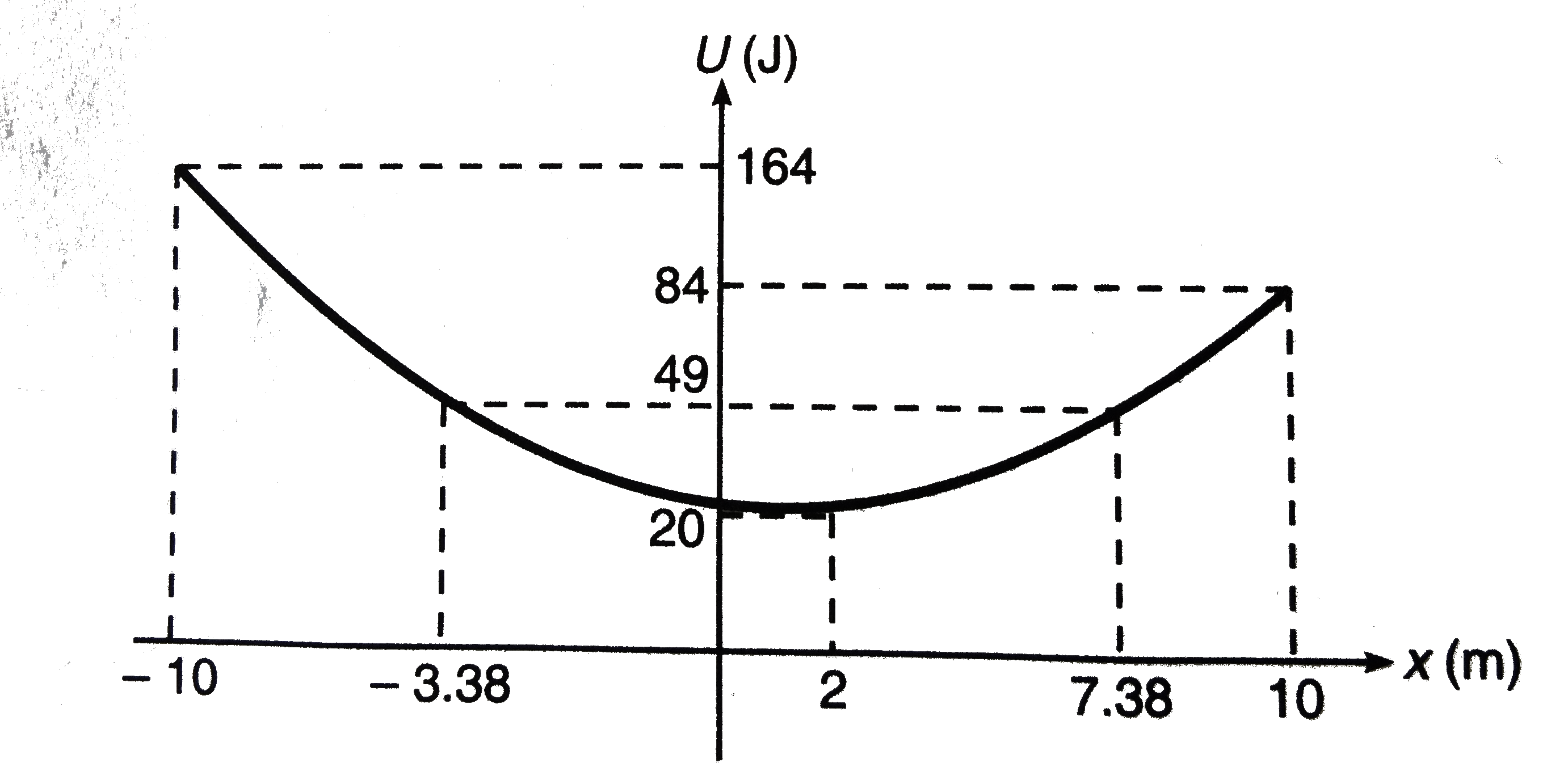(b) At `x=10m` `U=84J` at `x=-10m`, `U=164J`
and at `x=2m`, `U="minimum"=20J`
(c) and (d) Particle will move between the points where its kinetic energy becomes zero or its potential energy is equal to its mechanical energy.
Thus, `49=20 + (x-2)^(2)`
or `(x-2)^(2) =29`
or `x-2 =+-sqrt(29) =+-5.38m`
`:. x=7.38m` and `-3.38m`
or the particle will move between `x=-3.38 m` and `x=7.38 m`
(e) and (f) Maximum kinetic energy is at `x=2m`, where the potential energy is minimum and this maximum kinetic energy is,
`K_("max")=E-U_("min")=49-20`
`=29 J`
(g) `F =-(dU)/(dx) =-2(x-2) =2(2-x)`
(h) `F(x) =0`, at `x=2.0m`
where potential energy is minimum (the position of stable equilibrium).