In the figure shown the spring is compressed by 'x0' and released . Two block 'A' and 'B' of masses 'm' and '2m' respectively are attached at the ends of the spring. Blocks are kept on a smooth horizontal surface and released. Find the work done by the spring on 'A' by the time compression of the spring reduced to x02.

The correct Answer is:14kx20

Let the block A shift to left by x1 and block B shift to right by x2. The centre of mass of the two block system is at rest.
Hence mx1=2ms2.
or x2=x12…..(1)
and the spring force on either block is k(x0−[x1+x2]), where x0 is the initial compression in the spring.
Let the block A shift further left by dx1
∴work donw on block by spring is
dW=(k(x0−x1−x2)dx1.....(2)
=k(x0−x1−x12)dx1
∴Net work done
∫dW=x0/3∫x1=0k(x0−32x1)dx1=kx204
Ans.12kx20
Alternative Solution
Let the speeds of blocks A and B at the instant compression is x02 be vA andvB as shown in figure
[l0] natural length of spring ]

No external forces act on the system in the horizontal direction
Applying conservation of momentum in horizontal direction
Initial momentum = final momentum
0=m(−vA)+2mvB
or vA=2vB......(1)
from conservation of energy
12kx20=12k(x02)2+12mv2A+122mv2B....(2)
from (1) and (2) we get
12mv2A=14kx20
work done on block A by spring = change in kinetic energy of block A
=12mv2A=14kx20
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 53
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 54
8 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 51
7 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
54 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
Two blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View SolutionTwo blocks A and B of masses m and 2m, respectively , are connected by a massless spring of force constant k and are placed on a smooth horizontal plane. The spring is stretched by an amount x and then released . The relative velocity of the blocks when the spring comes to its natural length is

View Solution
Knowledge Check
A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0a block of mass 0.1 kg attached to a spring of spring constant400Nm pulled horizontally from x=0 tox1=10mm. Find the work done by the spring force
A2⋅10−2JB2⋅10−6JC3⋅10−6JD4⋅10−2JAll surfaces shown in figure are smooth. System is released with the spring instretched. In equilibrium, compression in the spring will be
 A2mgkB(M+m)g√2kCmg√2kDmgk
A2mgkB(M+m)g√2kCmg√2kDmgk
Two smooth blocks of mases m1andm2 attached with an ideal spring of stiffness k and kept on hrozontal surface. If m1 is projected with a horizontal velocity v0. Find the maximum compression of the spring.
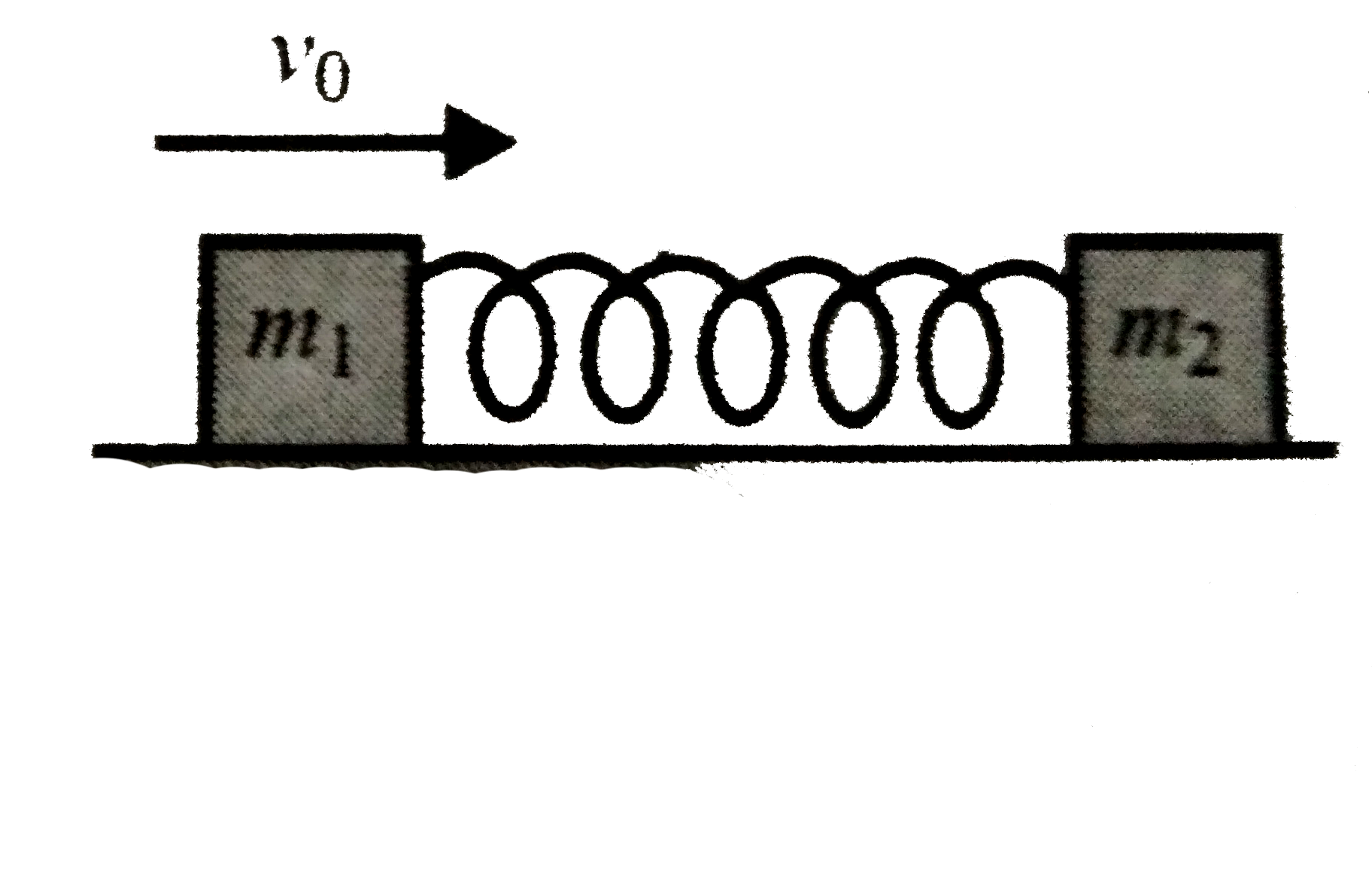
View SolutionTwo blocks of masses m and M connected by a light spring of stiffness k, are kept on a smooth horizontal surface as shown in figure. What should be the initial compression of the spring so that the system will be about to break off the surface, after releasing the block m1?
View SolutionAll surfaces shown in figure are smooth. System is released with the spring unstretched. In equilibrium, compression in the spring will be

View SolutionTwo blocks of masses 6 kg and 3 kg are attached to the two ends of a massless spring of spring constant 2π2N/m. If spring is compressed and released on a smooth horizontal surface then find the time period (in seconds) of each block.
View SolutionTwo blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
View Solution