Two smooth blocks of mases m1andm2 attached with an ideal spring of stiffness k and kept on hrozontal surface. If m1 is projected with a horizontal velocity v0. Find the maximum compression of the spring.
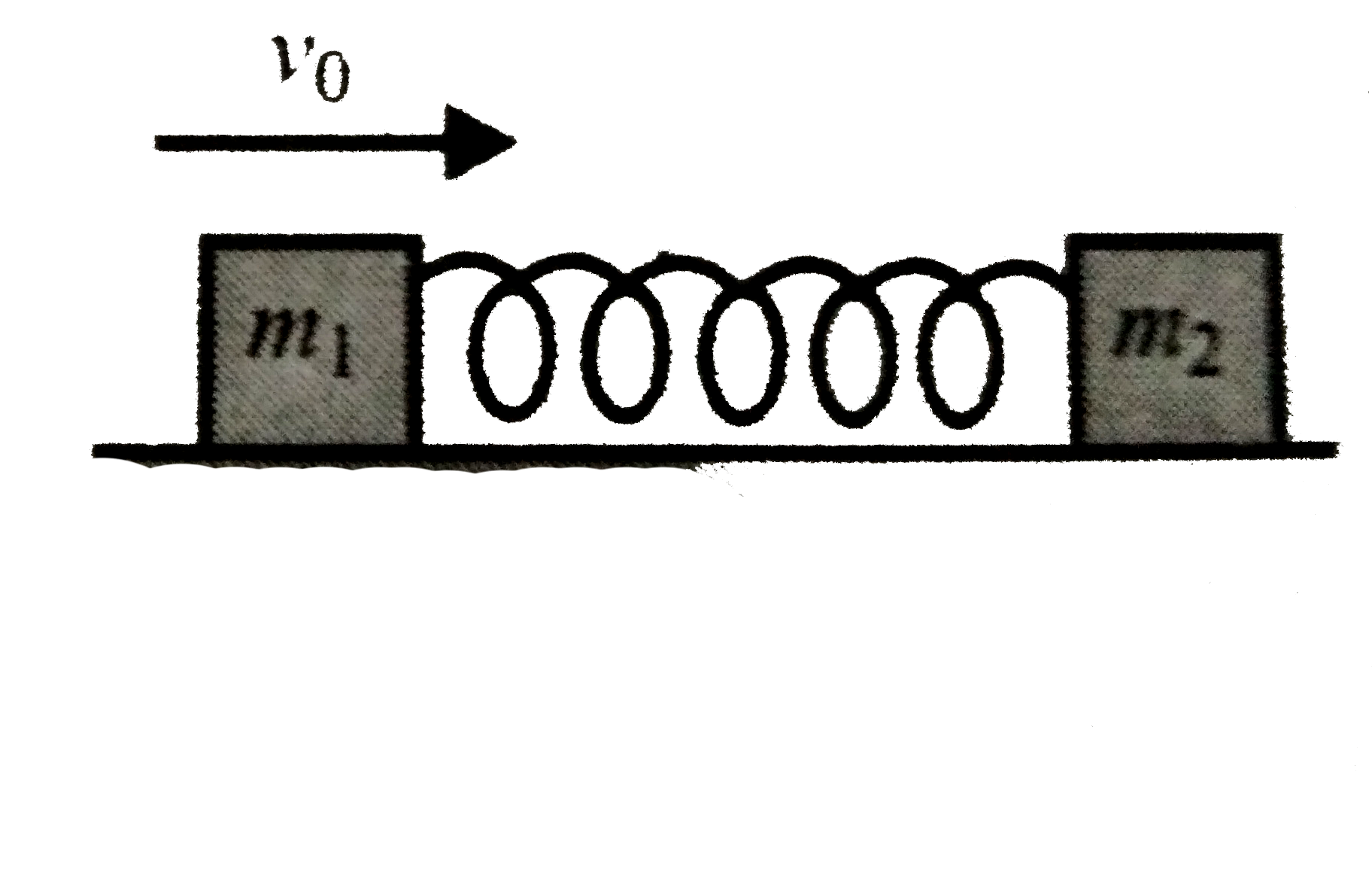
Method 1 (using ground frame method)
Decide system: Blocks and spring
Observation: no external force acting on system in horizontal direction.
Conclusion: linear momentum as well as mechanical energy of system will be move with common velocity.
Problem solving: Using conservation of linear momentum at initial time and at time of maximum compression of spring. Let the common velocity of system be V.
pi=m1v0+0 and pf=(m1+m2)V
As pi=pf⇒m1v0=(m1+m2)V.............i
Now using conservation of mechanical energy.
△K+△U=0
(Kf−Ki)+△Uspring=0
[12(m1+m2)V2−12m1v20]+12kx2=0...........i
From i and ii we get
x=⎡⎣√m1m2(m1_m2)k⎤⎦v0
Method 2: (work energy theorem from centre of mass frame)
The linear momentum of system from CM frame is zero and no external force is acting on the system. We can apply work energy theorem from CM frame
Wext+W∫=△Kcm=(Kf−Ki)cm .............iii
Initial kinetic energy of system w.r.t CM
(Ki)cm=12(m1m2m1+m2)v20
Final kinetic energy of system w.r.t CM
(Kf)cm=12μ(vnet)2_(final)=0
as both the blocks move with common velocity hence (vnet)final=0 which gives (Kf)cm=0
Hence from 1
0+(−12kx2)0−12(m1m2m1+m2)v20
⇒x=⎡⎣√m1m2(m1+m2)k⎤⎦v0
Topper's Solved these Questions
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Solved Examples
Explore 13 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Exercise 1.1
Explore 20 Videos
- CALORIMETRYBook:CENGAGE PHYSICSChapter:CALORIMETRYExercise:Solved Example
Explore 13 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
Similar Questions
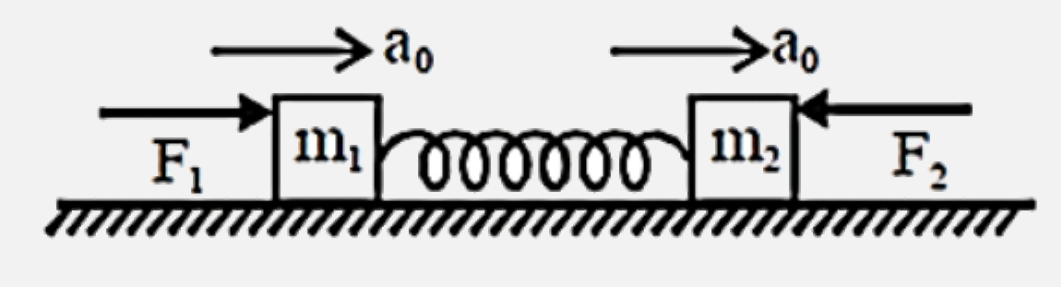
Two blocks of masses m1andm2 being connected with a light spring of stiffness k are driven with forces F1andF2 on a smooth horizontal plane.
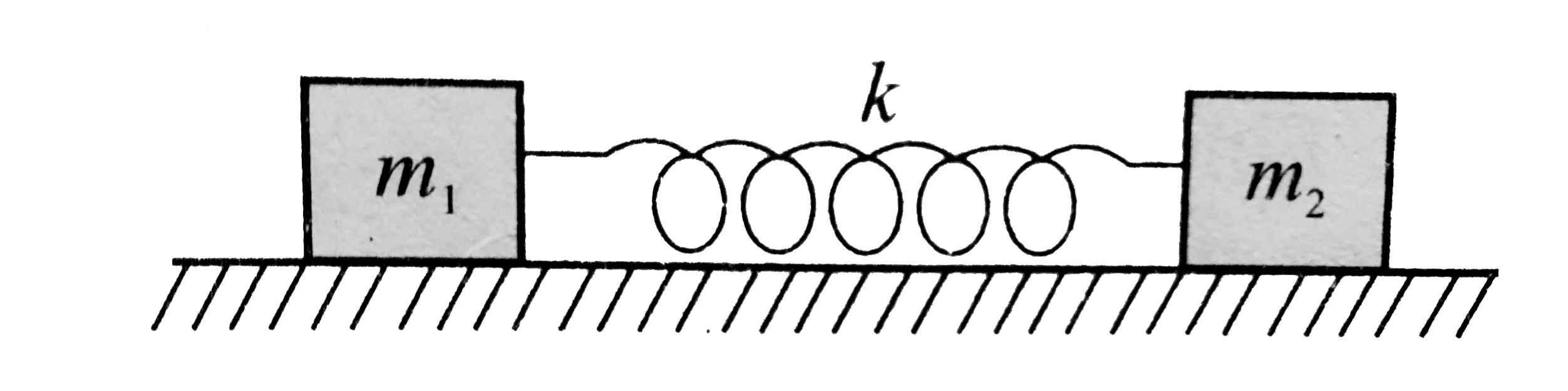
View SolutionTwo blocks of masses m1 and m2 interconnect with a spring of stiffness K, are kept on as smooth horizontal surface. Find out the ratio of velocity, displacement, kinetic energy and acceleration block with mass m1 of block with mass m2.
View Solution
Knowledge Check
Two blocks of masses m1=1kg and m2 = 2kg are connected by a spring of spring constant k = 24 N/m and placed on a frictionless horizontal surface. The block m1 is imparted an initial velocity v0 = 12cm/s to the right. The amplitude of osciallation is
A2 cmB1 cmC3 cmD4 cmTwo blocks m1 and m2 are pulled on a smooth horizontal surface, and are joined together with a spring of stiffness k as shown in Fig. Suddenly, block m2 receives a horizontal velocity v0, then the maximum extension xm in the spring is
 Av0√m1m2m1+m2Bv0√2m1m2((m1+m2)k)Cv0√m1m22(m1+m2)kDv0√m1m2(m1+m2)k
Av0√m1m2m1+m2Bv0√2m1m2((m1+m2)k)Cv0√m1m22(m1+m2)kDv0√m1m2(m1+m2)kA block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
 A14√mv2kB√mv2kC12√mv2kD2√mv2k
A14√mv2kB√mv2kC12√mv2kD2√mv2k
Two blocks of masses m and M connected by a light spring of stiffness k, are kept on a smooth horizontal surface as shown in figure. What should be the initial compression of the spring so that the system will be about to break off the surface, after releasing the block m1?
View SolutionAn external unknown horizontal force F pulls a smooth block of mass m attached with an ideal spring of stiffness k. Block is initially at rest and spring is relaxed. Find the work done (in J) by the force F, when the block moves with a velocity v and the deformation of the spring is x (k = 25 N/m, v = 1 m/s, m = 1 kg, x =20 cm)
View SolutionTwo blocks of mass m1 and m2 (m1<m2) are connected with an ideal spring on a smooth horizontal surface as shown in figure. At t = 0 m1 is at rest and m2 is given a velocity v towards right. At this moment, spring is in its natural length. Then choose the correct alternative :

View SolutionA block attached with an ideal spring is kept on a smooth horizontal surface. Now the free end of the spring is pulled with a constant velocity u horizontally. Then the maximum energy stored in the spring and bock system during subsequent motion is :
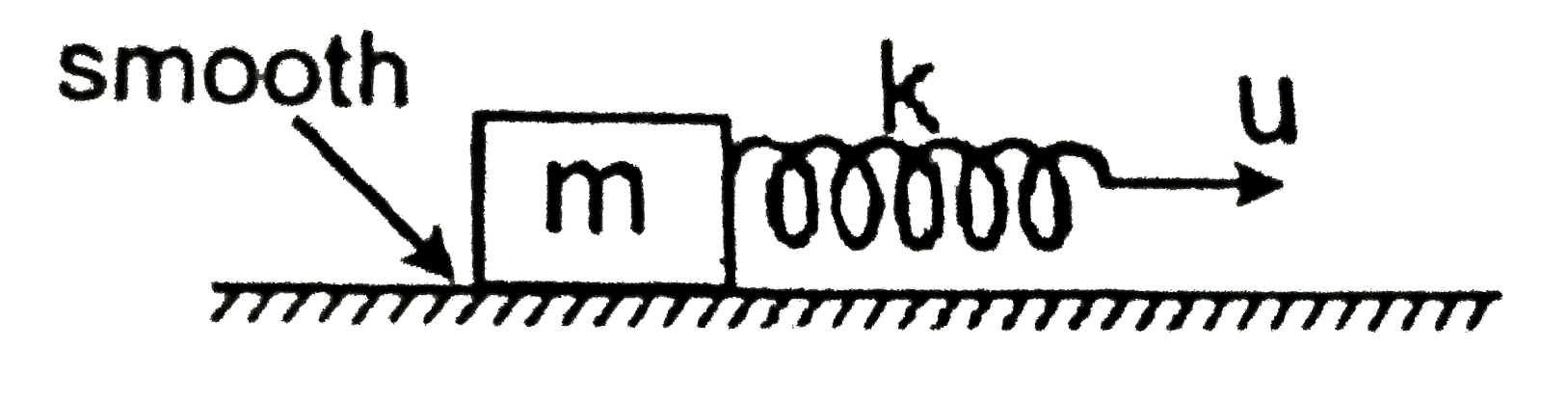
View SolutionTwo blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
View Solution

