Find the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is λ
We split the semicircular arc into small segments ds. We have point charge on each segment as λds. The electric field due to this small segment of charges, from Coulomb's law,
dE=14πε0λdsR2
Each little portion of the arc will give dE, in a different direction. We must therefore take components in order to find the total field at the centre.
Here X-component of the electric field is zero. This is the result of the fact that dEx shown in the figure will be cancelled by the contribution from a symmetrically placed ds on the left half of the arc.
Hence we need only to compute dEy which is vertically downward.
dEy=λdscosθ4πε0R2=λ(Rdθ)cosθ4πε0R2
Ey=∫dEy=λ4πε0Rπ/2∫−π/2cosθdθ=λ2πεθR

Similar Questions
Electric field at centre of a uniforly charged semicirlce of radius a is
View SolutionFind the centre of mass of a uniform semicircular ring of radius R and mass M.
View SolutionFind the electric field at centre of semicircular ring shown in figure .
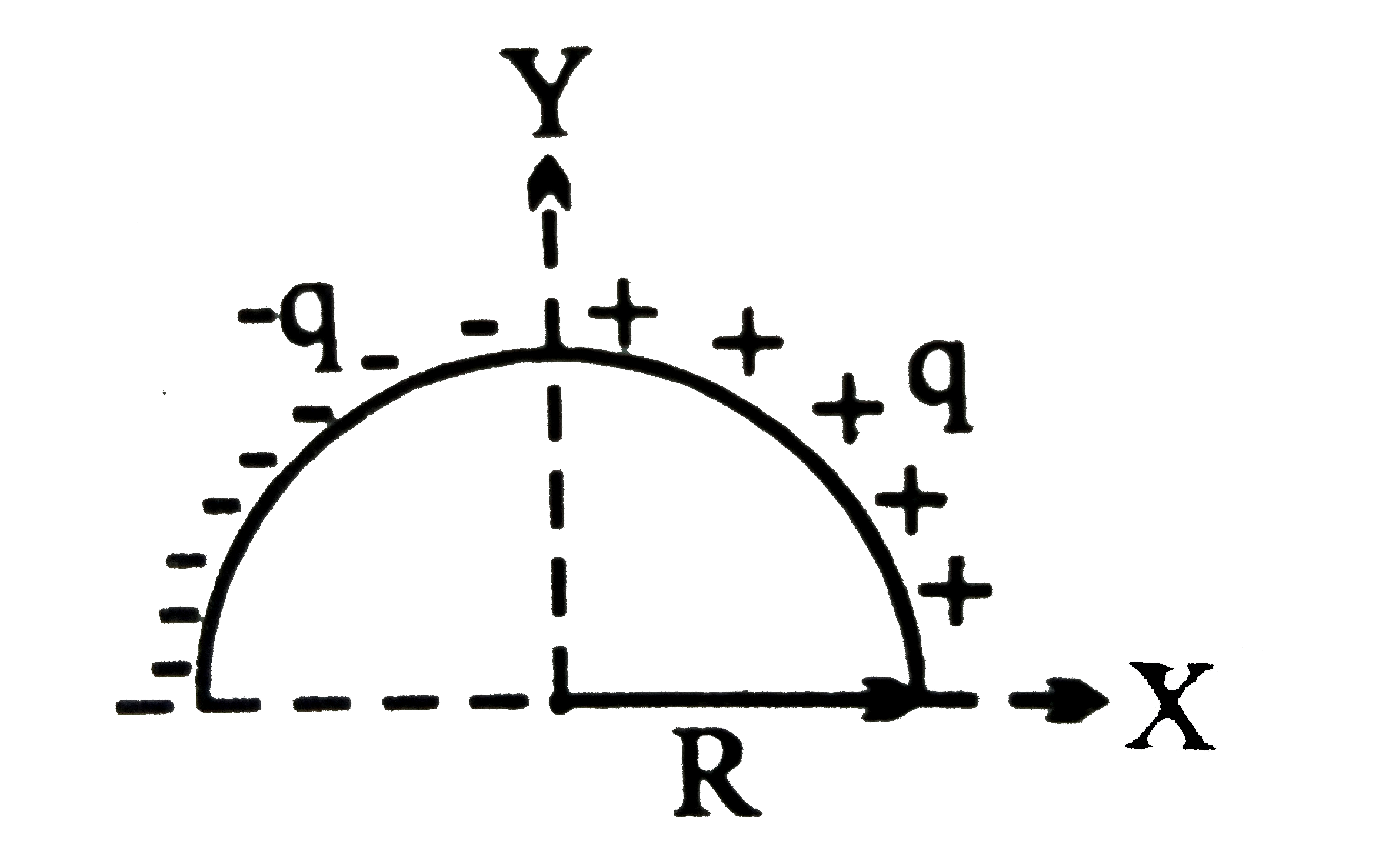 .
.
View SolutionElectric field at centre O of semicircule of radius 'a' having linear charge density λ given is given by

View SolutionElectric field at the centre of uniformly charge hemispherical shell of surface charge density σ is σnε0 then find the value of n.
View SolutionThe electric field at 2R from the centre of a uniformly charged non - conducting sphere of rarius R is E. The electric field at a distance R2 from the centre will be
View Solution(a) Using Gauss's law, derive an expression for the electric field intensity at any point outside a uniformly charged thin spherical shell of radius R and charge density σC/m2. Draw the field lines when the charge density of the sphere is (i) positive, (ii) negative.
(b) A uniformly charged conducting sphere of 2.5 m in diameter has a surface charge density of 100 μC/m2. Calculate the
(i) charge on the sphere
(ii) total electric flux passing through the sphere.
View SolutionElectric field at a point of distance r from a uniformly charged wire of infinite length having linear charge density λ is directly proportional to
View SolutionFind the electric field due to an infinitely long cylindrical charge distribution of radius R and having linear charge density λ at a distance half of the radius from its axis.
View SolutionA point charge q0 is placed at the centre of uniformly charges ring of total charge Q and radius R. If the point charge is slightly displaced with negligible force along axis of the ring then find out its speed when it reaches a large distance.
View Solution
