A point charge q0 is placed at the centre of uniformly charges ring of total charge Q and radius R. If the point charge is slightly displaced with negligible force along axis of the ring then find out its speed when it reaches a large distance.
To solve the problem, we will follow these steps:
Step 1: Understand the System
We have a point charge q0 placed at the center of a uniformly charged ring with total charge Q and radius R. When the charge q0 is slightly displaced along the axis of the ring, we need to find its speed when it reaches a large distance.
Step 2: Calculate the Electric Potential at the Center
At the center of the ring, the electric potential V due to the uniformly charged ring is given by the formula:
V=kQR
where k is Coulomb's constant.
Step 3: Work Done on the Charge
When the charge q0 is displaced from the center, it will experience a change in potential energy. The work done W on the charge when it moves from the center to a large distance is equal to the change in potential energy, which can be expressed as:
W=q0⋅V
Substituting the expression for V:
W=q0⋅kQR
Step 4: Relate Work Done to Kinetic Energy
According to the work-energy theorem, the work done on the charge is equal to the change in kinetic energy. If we assume the charge starts from rest, the initial kinetic energy is zero, so:
W=ΔKE=12mv2
where m is the mass of the charge q0 and v is its final speed.
Step 5: Set Up the Equation
From the previous steps, we can equate the work done to the change in kinetic energy:
q0⋅kQR=12mv2
Step 6: Solve for Speed v
Rearranging the equation to solve for v:
12mv2=q0⋅kQR
v2=2q0kQmR
v=√2q0kQmR
Final Answer
The speed of the charge q0 when it reaches a large distance is given by:
v=√2q0kQmR
---
We have a point charge q0 placed at the center of a uniformly charged ring with total charge Q and radius R. When the charge q0 is slightly displaced along the axis of the ring, we need to find its speed when it reaches a large distance.
At the center of the ring, the electric potential V due to the uniformly charged ring is given by the formula:
V=kQR
where k is Coulomb's constant.
When the charge q0 is displaced from the center, it will experience a change in potential energy. The work done W on the charge when it moves from the center to a large distance is equal to the change in potential energy, which can be expressed as:
W=q0⋅V
Substituting the expression for V:
W=q0⋅kQR
According to the work-energy theorem, the work done on the charge is equal to the change in kinetic energy. If we assume the charge starts from rest, the initial kinetic energy is zero, so:
W=ΔKE=12mv2
where m is the mass of the charge q0 and v is its final speed.
From the previous steps, we can equate the work done to the change in kinetic energy:
q0⋅kQR=12mv2
Rearranging the equation to solve for v:
12mv2=q0⋅kQR
v2=2q0kQmR
v=√2q0kQmR
The speed of the charge q0 when it reaches a large distance is given by:
v=√2q0kQmR
Topper's Solved these Questions
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Problems
Explore 22 Videos
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Exercise-1 Section (A)
Explore 9 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCE ENGLISHChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
Similar Questions
Find out energy stored in the electric field of uniformly charged thin spherical shell of total charge Q and radius R.
View SolutionFind the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is λ
View SolutionThe maximum electric field intensity on the axis of a uniformly charged ring of charge q and radius R will be
View SolutionA charge Q is placed at the centre of the line joining two point charges +q and +q as shown in figure. The ratio of charges Q and q is

View SolutionConsider a uniformly charged ring of radius R. Find the point on the axis where the electric field is maximum.
View SolutionA thin circular wire of radius r has a charge Q. If a point charge q is placed at the centre of the ring, then find the increase in tension in the wire.
View SolutionThe electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
View SolutionA short dipole is placed on the axis of a uniformly charged ring (total charge -Q, radius R) at a distance R√2 from centre of ring as shown in figure. Find the Force on the dipole due to that ring

View SolutionA charge q is placed at the point P as shown in figure on the axis of the ring of elemental thickness 't' and radius R then flux through the ring is :-
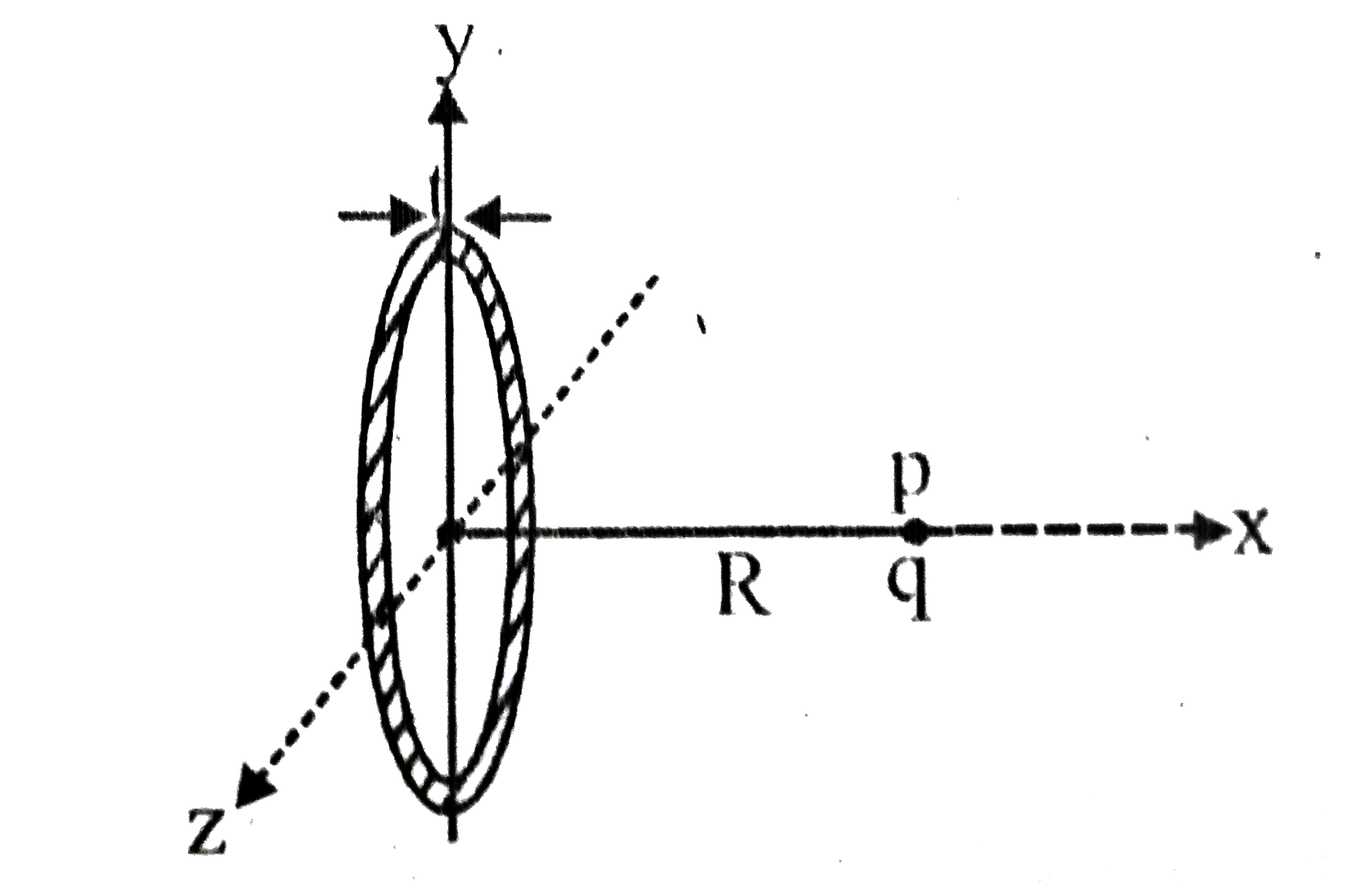
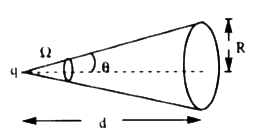
View SolutionA point charge q is placed at a distance d from the centre of a circular disc of radius R. Find electric flux flowing through the disc due to that charge
View Solution

