Consider a uniformly charged ring of radius R. Find the point on the axis where the electric field is maximum.
To find the point on the axis of a uniformly charged ring where the electric field is maximum, we can follow these steps:
Step 1: Understand the Configuration
Consider a uniformly charged ring of radius R with total charge Q. We are interested in the electric field at a point P located on the axis of the ring at a distance x from its center.
Step 2: Expression for Electric Field
The electric field E at point P due to the charged ring can be expressed as:
E=kQx(R2+x2)3/2
where k is Coulomb's constant.
Step 3: Differentiate the Electric Field
To find the point where the electric field is maximum, we need to differentiate E with respect to x and set the derivative equal to zero:
dEdx=0
Step 4: Apply the Quotient Rule
Using the quotient rule for differentiation, where u=kQx and v=(R2+x2)3/2:
dEdx=vdudx−udvdxv2
Calculating dudx and dvdx:
- dudx=kQ
- dvdx=32(R2+x2)1/2⋅2x=3x(R2+x2)1/2
Step 5: Set the Derivative to Zero
Now, we set the numerator of the derivative to zero:
(R2+x2)3/2⋅kQ−kQx⋅3x(R2+x2)1/2=0
Simplifying this gives:
(R2+x2)3/2=3x2(R2+x2)1/2
Step 6: Simplify the Equation
Dividing both sides by (R2+x2)1/2 (assuming R2+x2≠0):
(R2+x2)=3x2
Rearranging gives:
R2=2x2
Step 7: Solve for x
From the equation R2=2x2, we can solve for x:
x2=R22⟹x=R√2
Conclusion
Thus, the point on the axis of the uniformly charged ring where the electric field is maximum is at a distance:
x=R√2
---
Consider a uniformly charged ring of radius R with total charge Q. We are interested in the electric field at a point P located on the axis of the ring at a distance x from its center.
The electric field E at point P due to the charged ring can be expressed as:
E=kQx(R2+x2)3/2
where k is Coulomb's constant.
To find the point where the electric field is maximum, we need to differentiate E with respect to x and set the derivative equal to zero:
dEdx=0
Using the quotient rule for differentiation, where u=kQx and v=(R2+x2)3/2:
dEdx=vdudx−udvdxv2
Calculating dudx and dvdx:
- dudx=kQ
- dvdx=32(R2+x2)1/2⋅2x=3x(R2+x2)1/2
Now, we set the numerator of the derivative to zero:
(R2+x2)3/2⋅kQ−kQx⋅3x(R2+x2)1/2=0
Simplifying this gives:
(R2+x2)3/2=3x2(R2+x2)1/2
Dividing both sides by (R2+x2)1/2 (assuming R2+x2≠0):
(R2+x2)=3x2
Rearranging gives:
R2=2x2
From the equation R2=2x2, we can solve for x:
x2=R22⟹x=R√2
Thus, the point on the axis of the uniformly charged ring where the electric field is maximum is at a distance:
x=R√2
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBook:HC VERMA ENGLISHChapter:ELECTRIC FIELD AND POTENTIALExercise:question for short answer
Explore 14 Videos
- ELECTRIC FIELD AND POTENTIALBook:HC VERMA ENGLISHChapter:ELECTRIC FIELD AND POTENTIALExercise:Objective 1
Explore 9 Videos
- ELECTRIC FIELD AND POTENTIALBook:HC VERMA ENGLISHChapter:ELECTRIC FIELD AND POTENTIALExercise:worked out Examples
Explore 19 Videos
- ELECTRIC CURRENT THROUGH GASESBook:HC VERMA ENGLISHChapter:ELECTRIC CURRENT THROUGH GASESExercise:Short answer
Explore 6 Videos
- ELECTROMAGNETIC INDUCTIONBook:HC VERMA ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Questions for short answer
Explore 9 Videos
Similar Questions
The maximum electric field at a point on the axis of a uniformly charged ring is E0. At how many points on the axis will the magnitude of the electric field be E0/2.
View SolutionA uniformly charged disc of radius R with a total charge Q lies in the XY -plane. Find the electric field at a point at a point P, along the Z-a xis that passes through the centre of the discc perpendicular to its plane. Discuss the limit when R>>z.
Strategy : By treating the disc as a set of concentric uniformly charged rings, the problem could be solved by using the result obtained in example for ring. Consider a ring of radius of radius r' and thickness as shown in figure.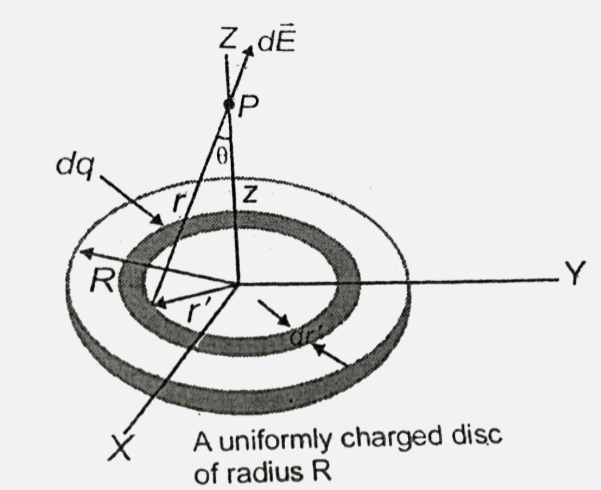
View SolutionFor a uniformly charged ring of radius R, the electric field on its exis has the largest magnitude at a distance h from its centre. Then value of h is :
View SolutionFigure shows a uniformly charged hemisphere of radius R. It has a volume charge density ρ. If the electric field at a point 2R, above the its center is E, then what is the electric field at the point 2R below its center?

View SolutionA ring of radius R is placed in the plane its centre at origin and its axis along the x-asis and having uniformly distributed positive charge. A ring of radius r(<<R) and coaxial with the larger ring is moving along the axis with constant velcity , then the variation of electrical flux (ϕ) passing through the smaller ring with position will be best represent by :
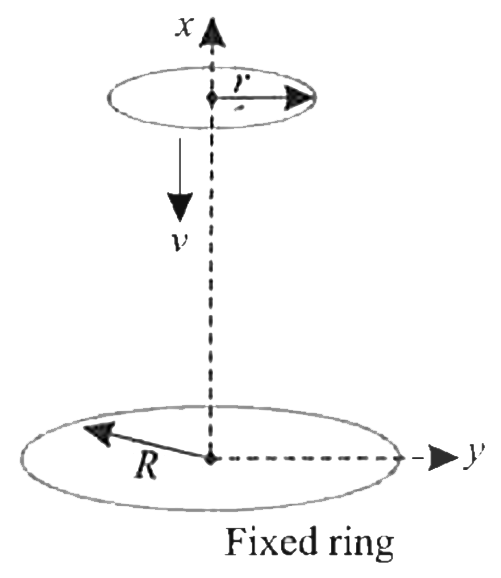
View SolutionAn unchanged conducting sphere of radius R is placed near a uniformly charge ring of radius R. Total charge on ring is Q. The centre of sphere lies on axis of ring and distance of centre of sphere from centre of ring is R

View SolutionA point charge of charge -q and mass m is released with negligible speed from a distance √3R on the axis of a fixed uniformly charged ring of charge Q and radius R. Find out its velocity when it reaches it reaches at the centre of the ring.

View SolutionAssertion : For a non-uniformly charged thin circular ring with net charge zero, the electric field at any point on axis of the ring is zero.
Reason : For a non-uniformly charged thin circular ring with net charge zero, the electric potential at each point on axis of the ring is zero.
View SolutionA uniformly charged ring of radius R is rotated about its axis with constant linear speed v of each of its particle. The ratio of electric field to magnetic field at a point P on the axis of the ring distant x=R from centre of ring is (c is speed of light )

View SolutionA charge of 5 nC is uniformly distributed on a ring of radius 4 cm. Find the potential at the axis at a distance of 3 cm from the center.
View Solution

