An electric field of 20N/C exists along the x-axis in space. Calculate the potential difference VB−VA where the points A and B are given by
a. A=(0,0),B=(4m,2m)
b. A=(4m,2m),B=(6m,5m)
To solve the problem, we will calculate the potential difference VB−VA for the two given pairs of points in an electric field of 20N/C along the x-axis.
Part (a): Points A and B
1. Identify the electric field and points:
- The electric field E=20N/C is directed along the x-axis.
- Point A is at (0,0) and point B is at (4m,2m).
2. Use the formula for potential difference:
VB−VA=−∫BAE⋅dr
Since the electric field is only along the x-axis, we can simplify the integral.
3. Evaluate the integral:
- The displacement vector dr can be expressed as (dx,dy). However, since the electric field is only in the x-direction, we only consider the x-component.
- The potential difference can be simplified to:
VB−VA=−E⋅(xB−xA)
where xA=0m and xB=4m.
4. Calculate the potential difference:
VB−VA=−20N/C⋅(4m−0m)=−20⋅4=−80V
Part (b): Points A and B
1. Identify the new points:
- Point A is at (4m,2m) and point B is at (6m,5m).
2. Use the same formula for potential difference:
VB−VA=−∫BAE⋅dr
3. Evaluate the integral:
- Again, we focus on the x-component:
VB−VA=−E⋅(xB−xA)
where xA=4m and xB=6m.
4. Calculate the potential difference:
VB−VA=−20N/C⋅(6m−4m)=−20⋅2=−40V
Final Answers:
- For part (a): VB−VA=−80V
- For part (b): VB−VA=−40V
1. Identify the electric field and points:
- The electric field E=20N/C is directed along the x-axis.
- Point A is at (0,0) and point B is at (4m,2m).
VB−VA=−∫BAE⋅dr
Since the electric field is only along the x-axis, we can simplify the integral.
- The displacement vector dr can be expressed as (dx,dy). However, since the electric field is only in the x-direction, we only consider the x-component.
- The potential difference can be simplified to:
VB−VA=−E⋅(xB−xA)
where xA=0m and xB=4m.
VB−VA=−20N/C⋅(4m−0m)=−20⋅4=−80V
1. Identify the new points:
- Point A is at (4m,2m) and point B is at (6m,5m).
VB−VA=−∫BAE⋅dr
- Again, we focus on the x-component:
VB−VA=−E⋅(xB−xA)
where xA=4m and xB=6m.
VB−VA=−20N/C⋅(6m−4m)=−20⋅2=−40V
- For part (a): VB−VA=−80V
- For part (b): VB−VA=−40V
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBook:HC VERMA ENGLISHChapter:ELECTRIC FIELD AND POTENTIALExercise:question for short answer
Explore 14 Videos
- ELECTRIC FIELD AND POTENTIALBook:HC VERMA ENGLISHChapter:ELECTRIC FIELD AND POTENTIALExercise:Objective 1
Explore 9 Videos
- ELECTRIC FIELD AND POTENTIALBook:HC VERMA ENGLISHChapter:ELECTRIC FIELD AND POTENTIALExercise:worked out Examples
Explore 19 Videos
- ELECTRIC CURRENT THROUGH GASESBook:HC VERMA ENGLISHChapter:ELECTRIC CURRENT THROUGH GASESExercise:Short answer
Explore 6 Videos
- ELECTROMAGNETIC INDUCTIONBook:HC VERMA ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Questions for short answer
Explore 9 Videos
Similar Questions
A uniform electric field of 400Vm is directed at 45∘ above the x-axis as shown in the figure. The potential difference VA−VB is given by
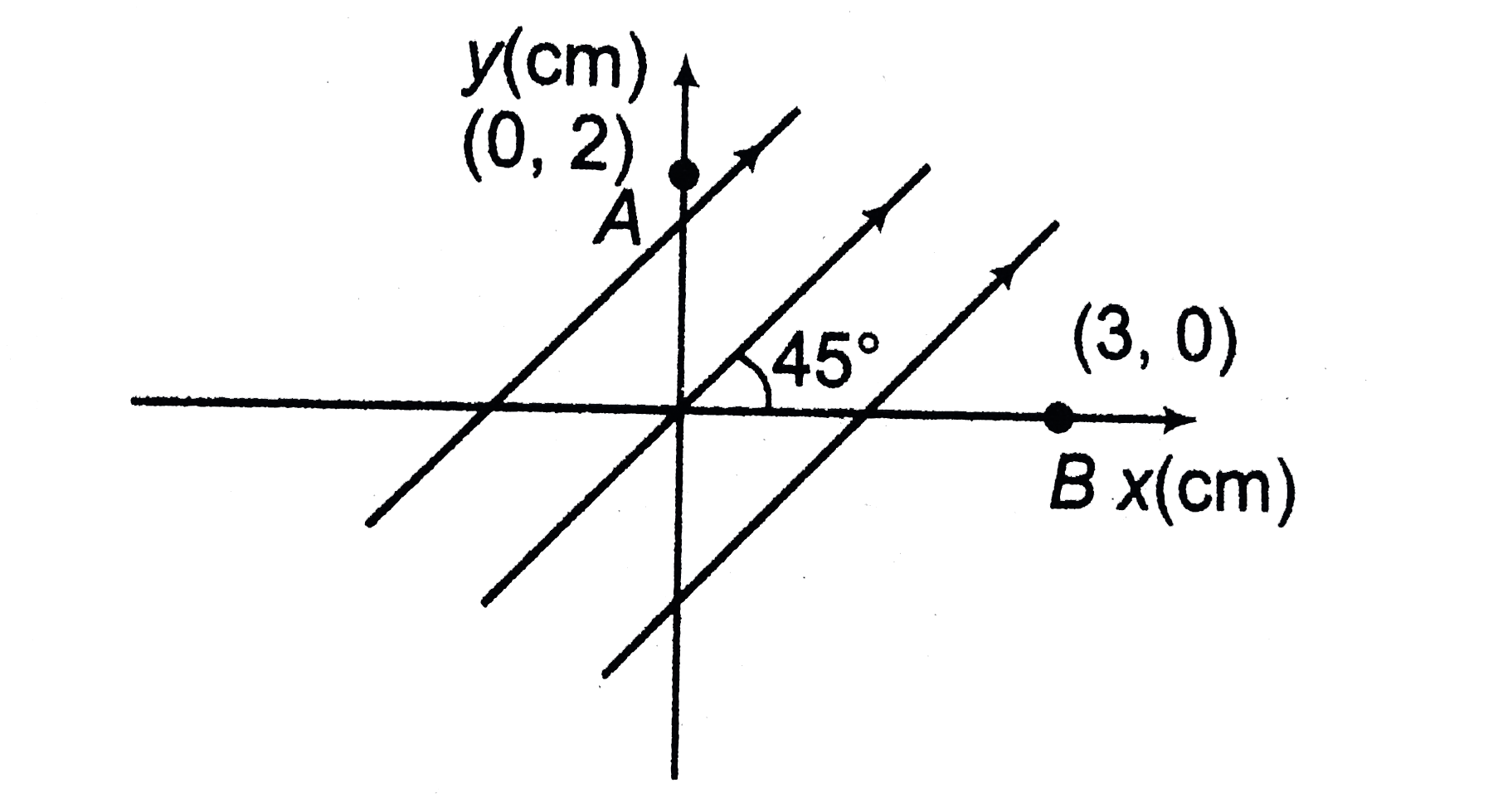
View SolutionAssume that an electric field →E=30x2ˆi exists in space. Then the potential difference VA−VO, where VO is the potential at the origin and VA the potential at x=2m is:
View SolutionA uniform electric field of 100V/m is directed at 3∘ with the positive x-axis as shown in figure. Find the potential difference VBA if OA=2m and OB=4m.

View SolutionA uniform electric field of 100V/m is directed at 30∘ with the positive x-axis as shown in figure. Find the potential difference VBA if OA=2m and OB=4m.

View SolutionA uniform electric field is along x-axis. The potential difference VA−VB=10V is between two points A (2m, 3m) and (4m, 8m). Find the electric field intensity.
View SolutionAssume that an electric field →E=30x2ˆi exists in space. Then the potential differences VA−V0 where V0 is the potential at the origin and VA, the potential at x=2m is
View SolutionA uniform electric field of 100 V/m is directed at 30∘ with the positive x-axis as shown in figure Find the potential difference Va−VA if OA = 2 m and OB = 4m.

View SolutionA uniform electric field is present in the positive x - direction. If the intensity of the field is 5NC−1 then find the potential difference (VB−VA) between two points A (0 m, 2 m) and B (5 m, 3 m).
View SolutionIn a certain region, electric field E exists along the x - axis which is uniform. Given B=2√3m and BC=4m. Points A, B, and C are in xy plane.
 .
.
Find the potential difference VA−VB between the points AandB.
View SolutionThe electric field in a certain region is given by E=5ˆi−3ˆjkv/m. The potential difference VB−VA between points a and B having coordinates (4, 0, 3) m and (10, 3, 0) m respectively, is equal to
View Solution

