A disc of radius R rotates at an angular velocity ω about the axis perpendicular to its surface and passing through its centre. If the disc has a uniform surface charge density σ, find the magnetic induction on the axis of rotation at a distance x from the centre. (Given R=3m, x=4m and μ0σω=20Tesla/m.)
To find the magnetic induction (magnetic field) on the axis of rotation at a distance x from the center of a rotating disc with a uniform surface charge density σ, we can follow these steps:
Step 1: Define the Problem
We have a disc of radius R rotating with an angular velocity ω and a uniform surface charge density σ. We want to find the magnetic induction at a distance x from the center along the axis of rotation.
Step 2: Consider a Differential Ring Element
To simplify the calculation, we can consider the disc as composed of an infinite number of concentric ring elements. Each ring has a radius r and thickness dr.
Step 3: Calculate the Area and Charge of the Ring
The area dA of the ring is given by:
dA=2πrdr
The charge dq on this ring is:
dq=σ⋅dA=σ⋅(2πrdr)
Step 4: Determine the Current due to the Rotating Ring
The ring rotates with angular velocity ω, which induces a current dI due to the moving charge:
dI=dqT=dq⋅ω2π=σ⋅(2πrdr)⋅ω2π=σ⋅ω⋅rdr
Step 5: Magnetic Field Contribution from the Ring
The magnetic field dB at a distance x from the center due to the current in the ring can be expressed using the Biot-Savart law:
dB=μ04π⋅dI⋅r(r2+x2)3/2
Substituting dI:
dB=μ04π⋅σ⋅ω⋅rdr⋅r(r2+x2)3/2=μ0σωr2dr4π(r2+x2)3/2
Step 6: Integrate to Find Total Magnetic Field
To find the total magnetic field B, we integrate dB from r=0 to r=R:
B=∫R0dB=∫R0μ0σωr2dr4π(r2+x2)3/2
Step 7: Solve the Integral
The integral can be solved using standard calculus techniques. The result of the integral gives:
B=μ0σω2(R2+2x2(R2+x2)3/2)
Step 8: Substitute Given Values
Given R=3m, x=4m, and μ0σω=20T/m:
B=202(32+2⋅42(32+42)3/2)
Calculating the values:
B=10(9+32(9+16)3/2)=10(41253/2)=10(41125)=410125=3.28T
Final Answer
The magnetic induction on the axis of rotation at a distance x=4m from the center is approximately 3.28T.
---
We have a disc of radius R rotating with an angular velocity ω and a uniform surface charge density σ. We want to find the magnetic induction at a distance x from the center along the axis of rotation.
To simplify the calculation, we can consider the disc as composed of an infinite number of concentric ring elements. Each ring has a radius r and thickness dr.
The area dA of the ring is given by:
dA=2πrdr
The charge dq on this ring is:
dq=σ⋅dA=σ⋅(2πrdr)
The ring rotates with angular velocity ω, which induces a current dI due to the moving charge:
dI=dqT=dq⋅ω2π=σ⋅(2πrdr)⋅ω2π=σ⋅ω⋅rdr
The magnetic field dB at a distance x from the center due to the current in the ring can be expressed using the Biot-Savart law:
dB=μ04π⋅dI⋅r(r2+x2)3/2
Substituting dI:
dB=μ04π⋅σ⋅ω⋅rdr⋅r(r2+x2)3/2=μ0σωr2dr4π(r2+x2)3/2
To find the total magnetic field B, we integrate dB from r=0 to r=R:
B=∫R0dB=∫R0μ0σωr2dr4π(r2+x2)3/2
The integral can be solved using standard calculus techniques. The result of the integral gives:
B=μ0σω2(R2+2x2(R2+x2)3/2)
Given R=3m, x=4m, and μ0σω=20T/m:
B=202(32+2⋅42(32+42)3/2)
Calculating the values:
B=10(9+32(9+16)3/2)=10(41253/2)=10(41125)=410125=3.28T
The magnetic induction on the axis of rotation at a distance x=4m from the center is approximately 3.28T.
Similar Questions
A metal disc of radius R rotates with an angular velcoity ω about an axis perpendiclar to its plane passing through its centre in a magnetic field B acting perpendicular to the plane of the disc. Calculate the induced emf between the rim and the axis of the disc.
View SolutionFind the electric field caused by a disc of radius a with a uniform surfce charge density σ (charge per unit area) at a point along the axis of the disc a distance x from its centre.
View Solution
Knowledge Check
One quarter sector is cut from a uniform circular disc of radius R. The sector has mass M. IT is made to rotate about a line perpendicular to its plane and passing through the centre of the original disc. Its moment of inertia about the axis of rotation is
AMR2/2BMR2/4CMR2/8D√2MR2
A disc of radius R rotates with constant angular velocity ω about its own axis. Surface charge density of this disc varies as σ=αr2, where r is the distance from the centre of disc. Determine the magnetic field intensity at the centre of disc.
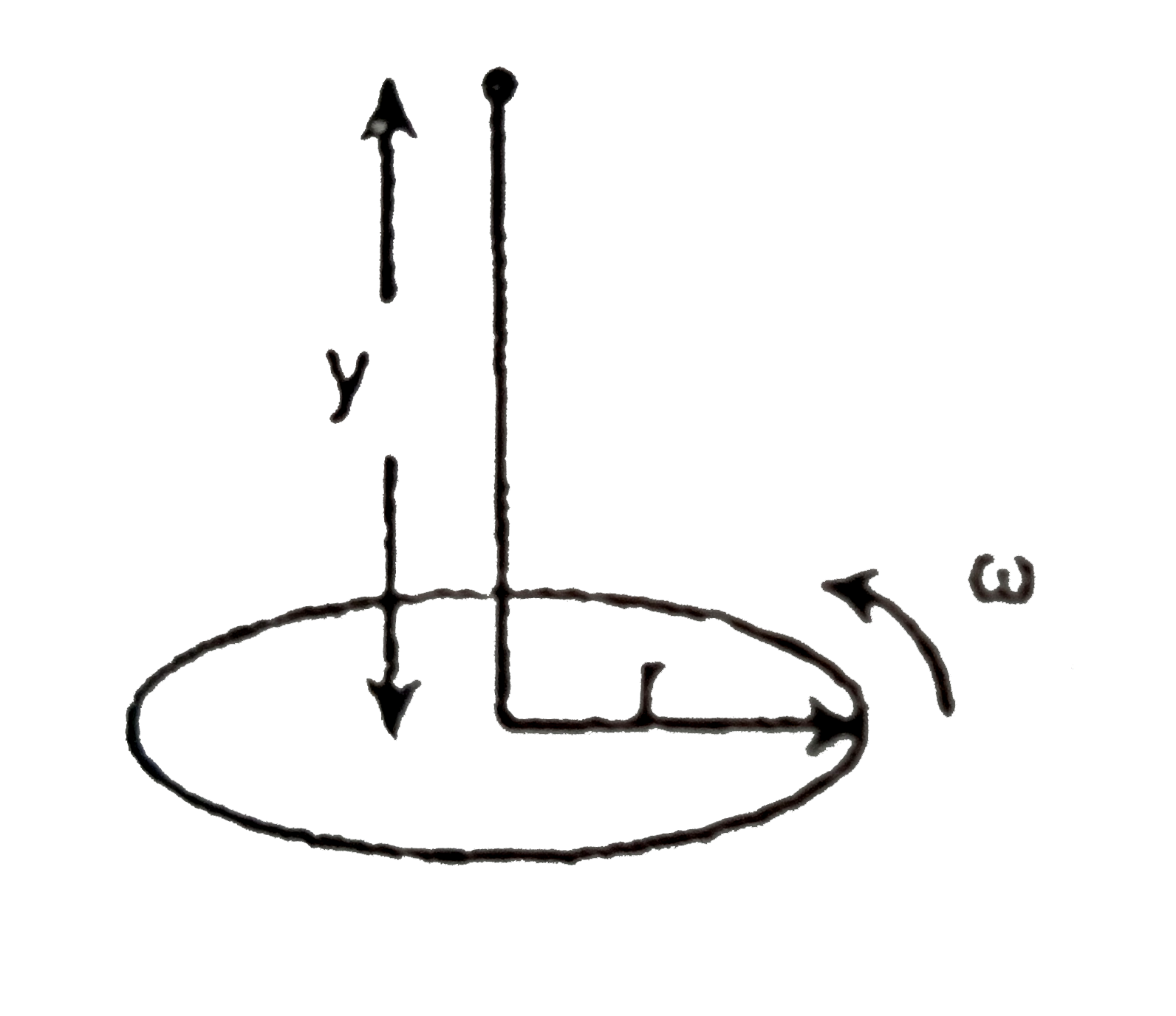
View SolutionCalculate the magnetic field at distance y from the centre of the axis of a disc of radius r and unifrom surface charge density σ, If the disc spins with angular velocity ω ?
View SolutionA metal disc of radius a rotates with a constant angular velocity ω about its axis. The potential difference between the center and the rim of the disc is (m = mass of electron, e = charge on electro)
View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionCircular disc of mass 2 kg and radius 1 m is rotating about an axis perpendicular to its plane and passing through its centre of mass with a rotational kinetic energy of 8 J. The angular momentum is (Js) is
View SolutionA sphere of radius R, uniformly charged with the surface charge density σ rotates around the axis passing through its centre at an angular velocity. (a) Find the magnetic induction at the centre of the rotating sphere. (b) Also, find its magnetic moment.
View Solution
