Circular disc of mass 2 kg and radius 1 m is rotating about an axis perpendicular to its plane and passing through its centre of mass with a rotational kinetic energy of 8 J. The angular momentum is (Js) is
8
4
2
1
The correct Answer is:B
To find the angular momentum of the circular disc, we can follow these steps:
Step 1: Determine the Moment of Inertia (I)
The moment of inertia I for a circular disc rotating about an axis perpendicular to its plane and passing through its center of mass is given by the formula:
I=12MR2
where M is the mass of the disc and R is the radius.
Given:
- Mass M=2kg
- Radius R=1m
Substituting the values:
I=12×2×(1)2=12×2×1=1kg m2
Step 2: Use the Rotational Kinetic Energy to Find Angular Velocity (ω)
The rotational kinetic energy K is given by the formula:
K=12Iω2
We know the rotational kinetic energy K=8J and we have calculated I=1kg m2.
Substituting the values into the equation:
8=12×1×ω2
This simplifies to:
8=12ω2
Multiplying both sides by 2:
16=ω2
Taking the square root:
ω=√16=4radians/second
Step 3: Calculate Angular Momentum (L)
The angular momentum L is given by the formula:
L=Iω
Substituting the values we found:
L=1×4=4Js
Final Answer
The angular momentum of the circular disc is 4Js.
---
The moment of inertia I for a circular disc rotating about an axis perpendicular to its plane and passing through its center of mass is given by the formula:
I=12MR2
where M is the mass of the disc and R is the radius.
- Mass M=2kg
- Radius R=1m
I=12×2×(1)2=12×2×1=1kg m2
The rotational kinetic energy K is given by the formula:
K=12Iω2
We know the rotational kinetic energy K=8J and we have calculated I=1kg m2.
8=12×1×ω2
This simplifies to:
8=12ω2
Multiplying both sides by 2:
16=ω2
Taking the square root:
ω=√16=4radians/second
The angular momentum L is given by the formula:
L=Iω
Substituting the values we found:
L=1×4=4Js
The angular momentum of the circular disc is 4Js.
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.3
15 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (A) Chapter Exercises
83 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.1
20 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
A flywheel of mass 0.2 kg and radius 10 cm is rotating with 5πrevs about an axis perpendicular to its plane passing through its centre. Calculate angular momentum and kinetic energy of flywheel.
View SolutionA quarter disc of radius R and mass m is rotating about the axis OO' (perpendicular to the plane of the disc) as shown. Rotational kinetic energy of the quarter disc is
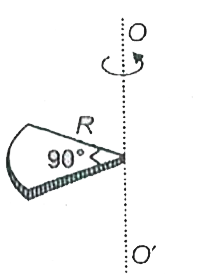
View Solution
Knowledge Check
One quarter sector is cut from a uniform circular disc of radius R. The sector has mass M. IT is made to rotate about a line perpendicular to its plane and passing through the centre of the original disc. Its moment of inertia about the axis of rotation is
AMR2/2BMR2/4CMR2/8D√2MR2
A circular disc of mass 100 g and radius 10 cm' is making 2 rps about an axis passing through its centre and perpendicular to its plane. Calculate its kinetic energy.
View SolutionOne quarter sector is cut from a uniform circular disc of radius R. This sector has mass M. It is made to rotate about a line perpendicular to its plane and passing through the centre of the original disc. It moment of inertia about the axis of rotation is.
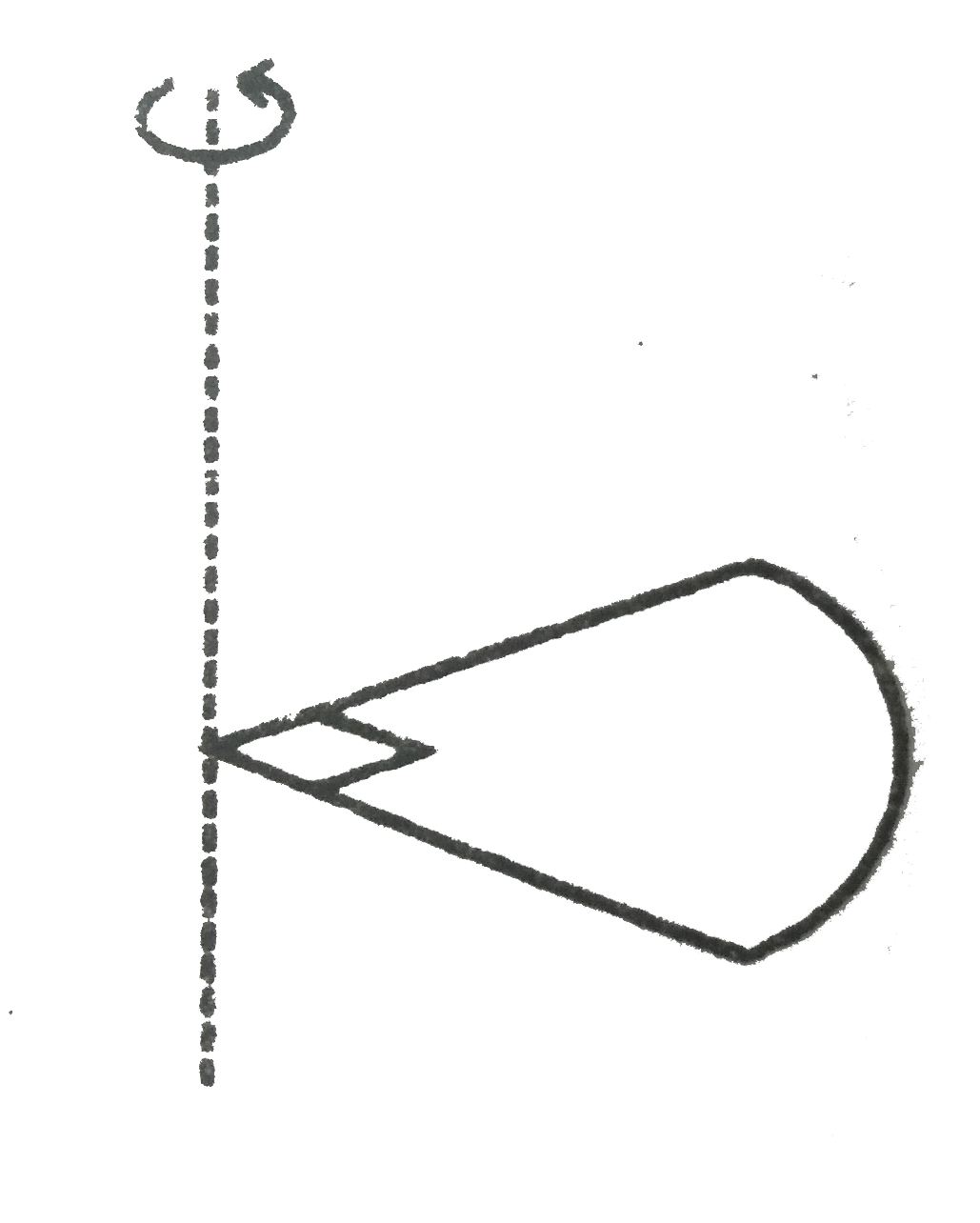 .
.
View SolutionA charge Q is uniformly distributed over the surface of non - conducting disc of radius R. The disc rotates about an axis perpendicular to its plane and passing through its centre with an angular to its plane and passing through its centre of the disc. If we keep both the amount of charge placed on the disc and its angular velocity to be constant and vary the radius of the disc then the variation of the magnetic induction at the centre of the disc will br represented by the figure:
View SolutionA uniform circular disc of mass 200 g and radius 4.0 cm is rotated about one of its diameter at an angular speed of 10 rad/s. Find the kinetic energy of the disc and its angular momentum about the axis of rotation.
View SolutionA ring of mass m and radius r rotates about an axis passing through its centre and perpendicular to its plane with angular velocity ω. Its kinetic energy is
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω . Another disc of same dimensions but of mass 14 M is placed gently on the first disc co-axially. The angular velocity of the system is
View SolutionA circular disc has a mass of 1kg and radius 40 cm. It is rotating about an axis passing through its centre and perpendicular to its plane with a speed of 10rev/s. The work done in joules in stopping it would be-
View Solution
