A door 1.6 m wide requires a force of 1 N to be applied at the free end to open or close it. The force that is required at a point 0.4 m distant from the hinges for opening or closing the door is
1.2 N
3.6 N
2.5 N
4 N
The correct Answer is:D
To solve the problem, we need to determine the force required to open or close a door when the force is applied at a distance of 0.4 m from the hinges, given that a force of 1 N is required at the free end (1.6 m from the hinges).
1. Understand the Torque Concept:
Torque (T) is defined as the product of the force (F) applied and the distance (r) from the pivot point (hinges). The formula for torque is:
T=F×r
2. Calculate the Torque at the Free End:
Given that a force of 1 N is applied at the free end of the door (1.6 m from the hinges):
T=1N×1.6m=1.6Nm
3. Set Up the Equation for the Force at 0.4 m:
Now, we need to find the force F that must be applied at a distance of 0.4 m from the hinges to produce the same torque of 1.6 Nm:
T=F×0.4m
4. Equate the Two Torque Values:
Since both torques must be equal for the door to open or close in the same manner:
F×0.4=1.6
5. Solve for F:
Rearranging the equation to solve for F:
F=1.60.4=4N
6. Conclusion:
The force required at a point 0.4 m distant from the hinges to open or close the door is 4 N.
Final Answer:
The required force is 4 N.
---
Torque (T) is defined as the product of the force (F) applied and the distance (r) from the pivot point (hinges). The formula for torque is:
T=F×r
Given that a force of 1 N is applied at the free end of the door (1.6 m from the hinges):
T=1N×1.6m=1.6Nm
Now, we need to find the force F that must be applied at a distance of 0.4 m from the hinges to produce the same torque of 1.6 Nm:
T=F×0.4m
Since both torques must be equal for the door to open or close in the same manner:
F×0.4=1.6
Rearranging the equation to solve for F:
F=1.60.4=4N
The force required at a point 0.4 m distant from the hinges to open or close the door is 4 N.
The required force is 4 N.
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.3
15 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (A) Chapter Exercises
83 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.1
20 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
Why is it easier to open a door by applying the force at the free end of it.
View Solutionforce F is applied at the topmost point of block of mass M. The force required to topple the block before sliding is (µ = coefficient of friction)
View SolutionThe breadth of an iron door is 2.4 m. If the minimum torque required to open the door is 50 Nm, what is the minimum force required to open the door?
View SolutionA block of mass m is pulled by a uniform chain of mass m tied to it by applying a force F at the other end of the chain.The tension at a point P which is at a distance of quarter of the length of the chain from the free end,will be

View SolutionA : It is very difficult to open or close a door if force is applied near the hinge.
R : The moment of applied force is minimum near the hinge.
View SolutionThe amount of force to be applied on the spanner at a length of 0.25 m from the bolt is 400 N. Find the torque to open a bolt.
View SolutionFigure a) shows a spring of force constant k clamped rigidly at once end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure b) shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in figure is stretched by the same force F.
(a) What is the maximum extension of the spring in the two cases ?
(b) If the mass in figure and the two masses in figure are released free, what is the period of oscillation in each case?
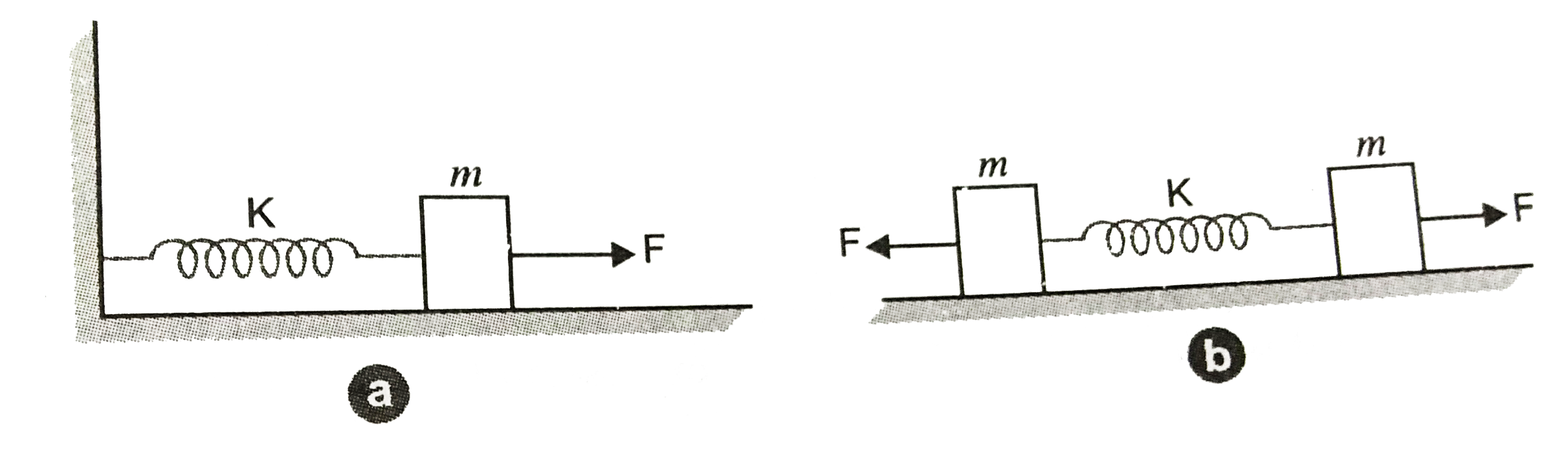
View SolutionFigure a) shows a spring of force constant k clamped rigidly at once end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure b) shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in figure is stretched by the same force F.
(a) What is the maximum extension of the spring in the two cases ?
(b) If the mass in figure and the two masses in figure are released free, what is the period of oscillation in each case?

View SolutionA rod of mass m and length l is hinged at one of its end A as shown in figure. A force F is applied at a distance x from A. The acceleration of centre of mass a varies with x as

View SolutionThe iron door of a building is 3m broad. It can be opened by applying a force of 100N normally at the middle of the door. Calculate (a) the torque needed to open the door, (b) the least force and its point of application to open the door.
View Solution
