One quarter sector is cut from a uniform circular disc of radius R. This sector has mass M. It is made to rotate about a line perpendicular to its plane and passing through the centre of the original disc. It moment of inertia about the axis of rotation is.
 .
.
12MR2
14MR2
18MR2
√2MR2
The correct Answer is:A
We cannot consider the quadrant as a single mass as the distance of different particles is different form the axis of rotation. So we take the help of calculus. Let us consider a segment as shown in figure. All masses lying in this segment are at a distance r form the axis and hence considered as a small differential mass dm. Let te thickness of the segment be dr.
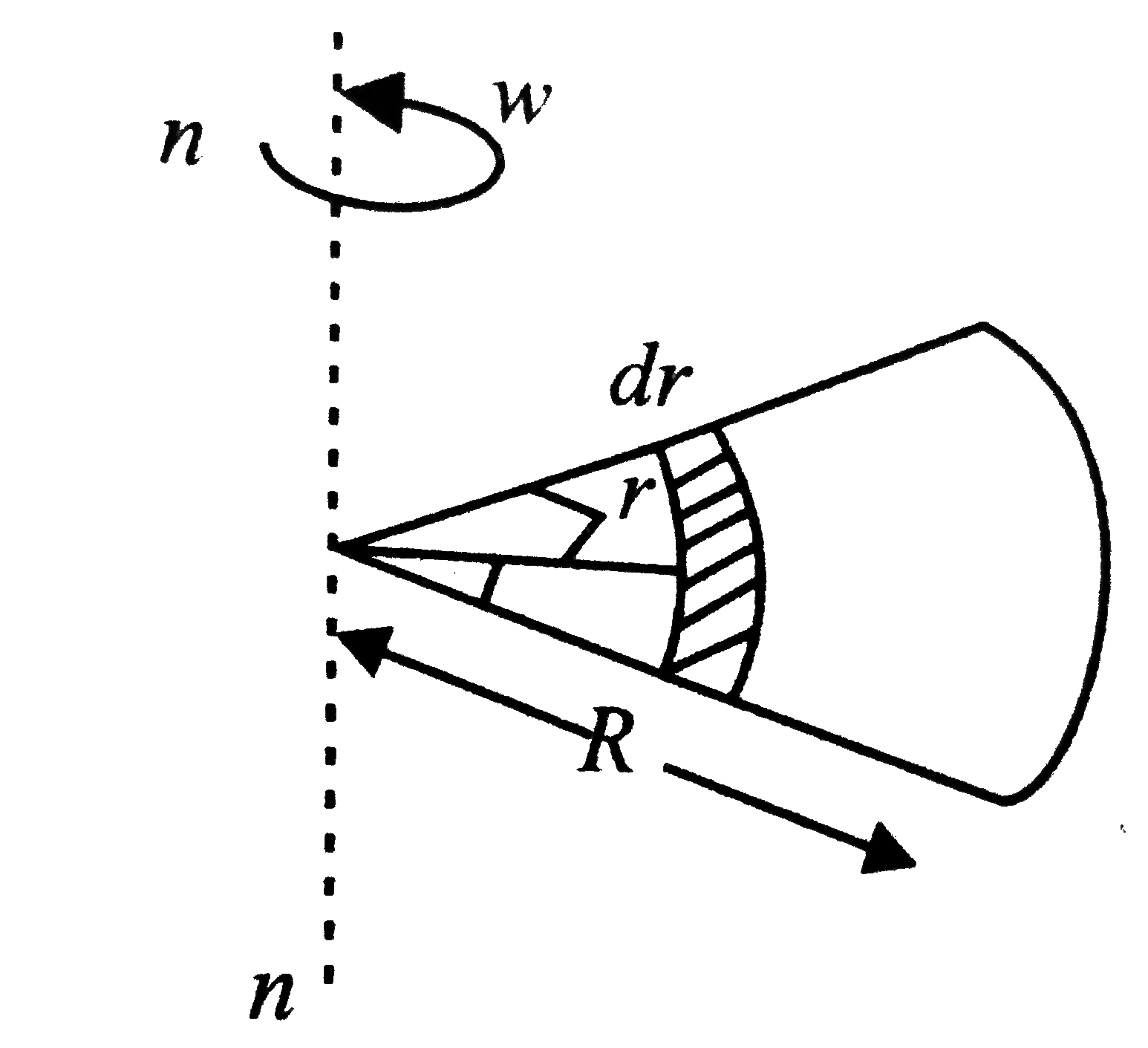
The mass per unit of the quadrant =MπR2/4=4MπR2
Area of the segment =14[π(r+dr)2−πr2]=14×2πrdr=πrdr2
Mass of the segment dm=πrdr2×4MπR2=2MR2r2rdr
MI of the segment about nn'=2MR2rdrxr22MR2r3dr
MI of the quadrant about nn'=∫R02MR2r2dr
2MR2×R44×MR22
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - MCQ_TYPE
14 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - AR_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - True/False
4 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
Moment of inertia of a uniform circular disc about a diameter is I. Its moment of inertia about an axis perpendicular to its plane and passing through a point on its rim will be.
View SolutionCircular disc of mass 2 kg and radius 1 m is rotating about an axis perpendicular to its plane and passing through its centre of mass with a rotational kinetic energy of 8 J. The angular momentum is (Js) is
View Solution
Knowledge Check
One quarter sector is cut from a uniform circular disc of radius R. The sector has mass M. IT is made to rotate about a line perpendicular to its plane and passing through the centre of the original disc. Its moment of inertia about the axis of rotation is
AMR2/2BMR2/4CMR2/8D√2MR2
Consider a uniform square plate of of side and mass m. The moment of inertia of this plate about an axis perpendicular to its plane and passing through one of its corners is -
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionThe moment of inertia of thin uniform circular disc about one of the diameter is I. Its moment of inertia about an axis perpendicular to the circular surface and passing through its centre is
View SolutionThe moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the center is
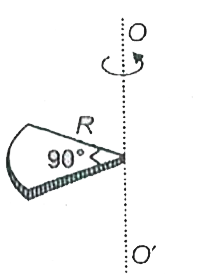
View SolutionA quarter disc of radius R and mass m is rotating about the axis OO' (perpendicular to the plane of the disc) as shown. Rotational kinetic energy of the quarter disc is
View SolutionThe moment of inertia of a uniform semicircularwire of mass M and radius r about a line perpendicular to the plane of the wire through the centre is :
View Solution
