A block of base 10cm×10cm and height 15cm is kept on an inclined plane. The coefficient of friction between them is √3. The inclination θ of this inclined plane from the horizontal plane is gradually increased from 0∘ Then
at θ=30∘ the block will start sliding down the plane
the block will remain at rest on the plane up to certain θ and ten it will topple
at θ=60∘ the block will start slidng down the plane and continue to do so at higher angles
at θ=60∘ the block will start sliding down the plane and on further increasing θ, it will topple at certain θ
The correct Answer is:B
To solve the problem, we need to analyze the forces acting on the block as the angle of inclination (theta) of the inclined plane is increased. We will determine the conditions under which the block will start sliding down the plane or topple over.
1. Identify the Forces Acting on the Block:
- The weight of the block (W = mg) acts vertically downward.
- The normal force (N) acts perpendicular to the inclined surface.
- The frictional force (F_friction) acts parallel to the surface and opposes the motion.
2. Resolve the Weight into Components:
- The component of the weight acting down the incline is W∥=mgsin(θ).
- The component of the weight acting perpendicular to the incline is W_{\perpendicular} = mg \cos(\theta) .
3. Determine the Normal Force:
- The normal force (N) is equal to the perpendicular component of the weight:
N=mgcos(θ)
4. Calculate the Frictional Force:
- The maximum static frictional force can be given by:
Ffriction=μN=μ(mgcos(θ))
- Given that the coefficient of friction μ=√3, we have:
Ffriction=√3(mgcos(θ))
5. Condition for Sliding:
- The block will start sliding when the downhill component of the weight exceeds the maximum static friction:
mgsin(θ)=√3(mgcos(θ))
- Dividing through by mg (assuming mg≠0):
sin(θ)=√3cos(θ)
- Dividing both sides by cos(θ):
tan(θ)=√3
- This implies:
θ=60∘
6. Condition for Toppling:
- To determine when the block will topple, we need to analyze the geometry of the block. The block will topple when the center of mass (CM) moves outside the base of the block.
- The height of the block is 15 cm, and the width is 10 cm. The center of mass is at a height of 152=7.5 cm.
- The distance from the edge of the base to the center of mass when tilted can be calculated using the tangent of the angle of inclination:
tan(α)=oppositeadjacent=7.55=32
- Thus, tan(α)=23.
7. Comparison of Angles:
- Since tan(60∘)=√3 and tan(α)=23, we see that:
tan(α)<tan(θ)
- This implies that the block will topple before it starts sliding.
Conclusion:
- The block will remain at rest until the angle θ reaches 60∘, at which point it will start to slide. However, it will topple before it can slide down the incline.
- The weight of the block (W = mg) acts vertically downward.
- The normal force (N) acts perpendicular to the inclined surface.
- The frictional force (F_friction) acts parallel to the surface and opposes the motion.
- The component of the weight acting down the incline is W∥=mgsin(θ).
- The component of the weight acting perpendicular to the incline is W_{\perpendicular} = mg \cos(\theta) .
- The normal force (N) is equal to the perpendicular component of the weight:
N=mgcos(θ)
- The maximum static frictional force can be given by:
Ffriction=μN=μ(mgcos(θ))
- Given that the coefficient of friction μ=√3, we have:
Ffriction=√3(mgcos(θ))
- The block will start sliding when the downhill component of the weight exceeds the maximum static friction:
mgsin(θ)=√3(mgcos(θ))
- Dividing through by mg (assuming mg≠0):
sin(θ)=√3cos(θ)
- Dividing both sides by cos(θ):
tan(θ)=√3
- This implies:
θ=60∘
- To determine when the block will topple, we need to analyze the geometry of the block. The block will topple when the center of mass (CM) moves outside the base of the block.
- The height of the block is 15 cm, and the width is 10 cm. The center of mass is at a height of 152=7.5 cm.
- The distance from the edge of the base to the center of mass when tilted can be calculated using the tangent of the angle of inclination:
tan(α)=oppositeadjacent=7.55=32
- Thus, tan(α)=23.
- Since tan(60∘)=√3 and tan(α)=23, we see that:
tan(α)<tan(θ)
- This implies that the block will topple before it starts sliding.
- The block will remain at rest until the angle θ reaches 60∘, at which point it will start to slide. However, it will topple before it can slide down the incline.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - MCQ_TYPE
14 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - AR_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - True/False
4 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
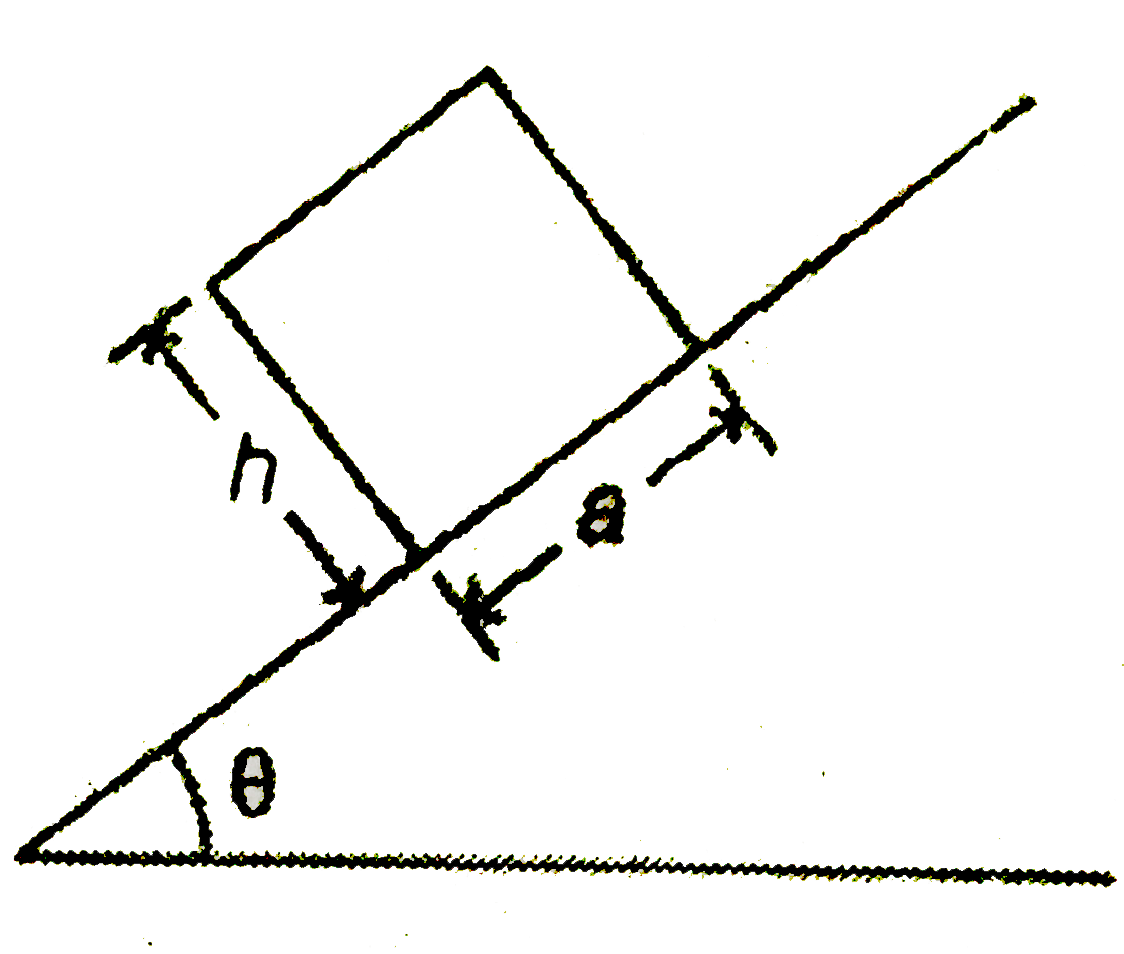
A block with a square base measuring a×a and height h, is placed on an inclined plane. The coefficient of friction is μ. The angle of inclination (θ) of the plane is gradually increased. The block will
View SolutionA mass placed on an inclined place is just in equilibrium. If μ is coefficient of friction of the surface, then maximum inclination of the plane with the horizontal is
View Solution
Knowledge Check
A block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination θ of the plane to the horizontal will the block just start to slide down the plane?
Aθ=tan−1μBθ=cos−1μCθ=sin−1μDθ=sec−1μ
A block of mass m is lying on an inclined plane. The coefficient of friction between the plane and the block is μ. The force (F1) required to move the block up the inclined plane will be:-
View SolutionA block of mass 2 kg slides down an incline plane of inclination 30°. The coefficient of friction between block and plane is 0.5. The contact force between block and plank is :
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionAn ice cube is kept on an inclined plane of angle 30∘. The coefficient to kinetic friction between the block and incline plane is the 1/√3. What is the acceleration of the block ?
View Solution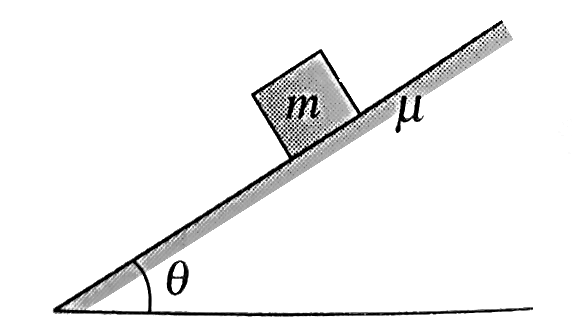 A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. If μ=34 then what will be frictional force (shear force) acting between the block and inclined plane when θ=30∘:
View Solution A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. For what value of θ will the block slide on the inclined plane:
View Solution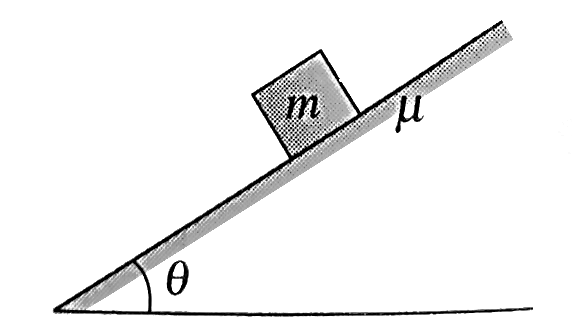 A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. If the entire system, were accelerated upward with acceleration a the angle of repose, would:
View Solution
