Calculate the magnetic field at distance y from the centre of the axis of a disc of radius r and unifrom surface charge density σ, If the disc spins with angular velocity ω ?
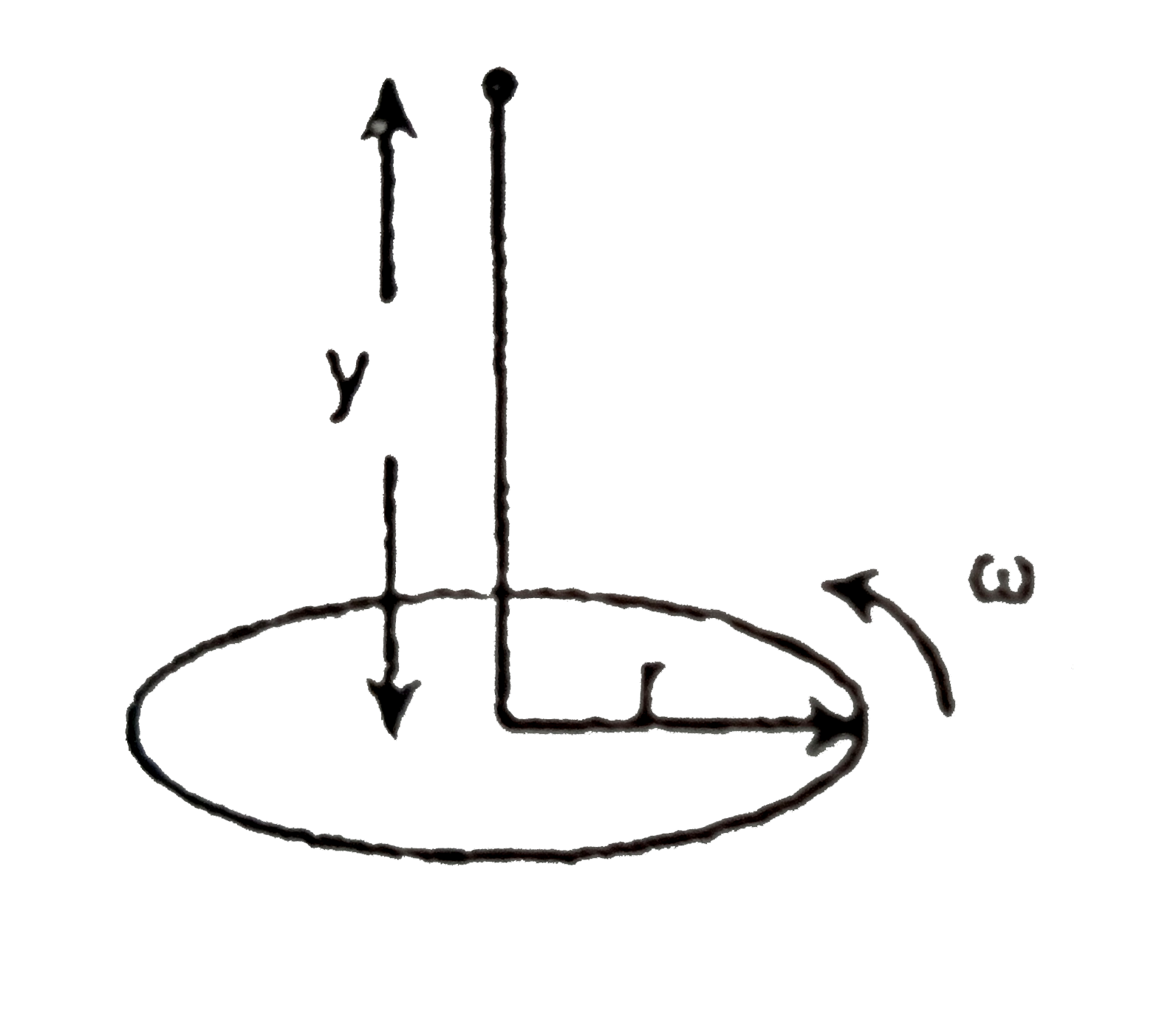
μ0σω3(r2−2y2√r2−y2+2y)
μ0σω2(r2+2y2√r2+y2)
μ0σω2(r2+2y2√r2+y2−2y)
2μ0σω3(r2+2y2√r2+y2−2y)
Charge on a ring of radius x and width dx
dq=(2πxdx)σ
Current, dI=dqdt=2πxσdxDt=ωσxdx
dB=μ0dIr22(x2+y2)3/2
B=μ0σω2(r2+2y2√r2+y2−2y)
Similar Questions
A disc of radius R rotates at an angular velocity ω about the axis perpendicular to its surface and passing through its centre. If the disc has a uniform surface charge density σ, find the magnetic induction on the axis of rotation at a distance x from the centre. (Given R=3m, x=4m and μ0σω=20Tesla/m.)
View SolutionFind the electric field caused by a disc of radius a with a uniform surfce charge density σ (charge per unit area) at a point along the axis of the disc a distance x from its centre.
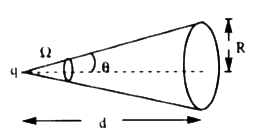
View SolutionA point charge q is placed at a distance d from the centre of a circular disc of radius R. Find electric flux flowing through the disc due to that charge
View SolutionA man of mass m stands on a horizontal platform in the shape of a disc of mass m and radius R, pivoted on a vertical axis thorugh its centre about which it can freely rotate. The man starts to move aroung the centre of the disc in a circle of radius r with a velocity v relative to the disc. Calculate the angular velocity of the disc.

View SolutionA charge Q is uniformly distributed over the surface of non - conducting disc of radius R. The disc rotates about an axis perpendicular to its plane and passing through its centre with an angular to its plane and passing through its centre of the disc. If we keep both the amount of charge placed on the disc and its angular velocity to be constant and vary the radius of the disc then the variation of the magnetic induction at the centre of the disc will br represented by the figure:
View SolutionMoment of inertia of a disc about an axis parallel to diameter and at a distance x from the centre of the disc is same as the moment of inertia of the disc about its centre axis. The radius of disc is R. The value of x is
View SolutionA cockroach is moving with velocity v in anticlockwise direction on the rim of a disc of radius R of mass m. The moment of inertia of the disc about the axis is I and it is rotating in clockwise direction with an angular velocity ω. If the cockroach stops, the angular velocity of the disc will be
View SolutionA metal rod of resistance R is fixed along a diameter of a conducting ring of radius r. There is a magnetic field of magnitude B perpendicular to the plane of the loop. The ring spins with an angular velocity ω about its axis. The centre of the ring is joined to its rim by an external wire W. The ring and W have no resistance. The current in W is
View SolutionWe have a disc of neglligible thickness and whose surface mass density varies as radial distance from centre as σ=σ0(1+rR), where R is the radius of the disc. Specific heat of the material of the disc isC.
Disc is given an angular velocity ω0 and placed on a horizontal rough surface such that the plane of the disc is parallel to the surface. Coefficient of friction between disc and suface is μ. The temperature of the disc is T0.
Answer the following question on the base of information provided in the above paragraph
If the kinetic energy lost due to the friction between disc and surface is absorbed by the disc the moment heat is generated, by the mass lying at the point where the energy is lost. Assume that there is no radial heat flow in betwen disc particles. Rate of change in temperature at a point lying at r distance away from centre with time, before disc stops rotating, will be (α-magnitude of angular acceleration of rod)
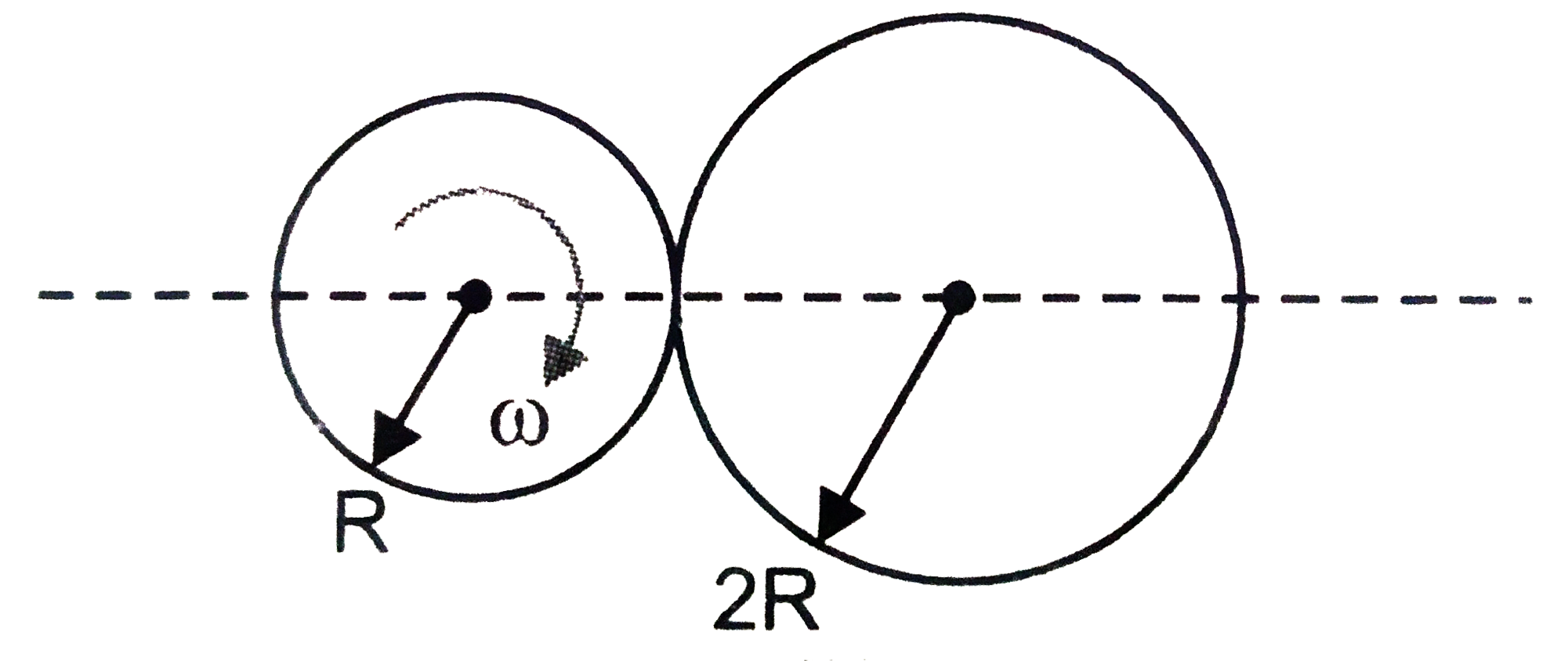
View SolutionTwo discs of radii Rand2R are pressed against each other. Initially, disc with radius R is rotating with angular velocity ω and other disc is stationary. Both discs are hinged at their respective centres and are free to rotate about them. Moment of inertia of smaller disc is I and of bigger disc is 2I about their respective axis of rotation. Find the angular velocity of bigger disc after long time.
View Solution
