Resistances R, 2R, 4R, 8R......∫fyare connected in parallel. What is their equivalent resistance?
External forces acting on the system are weights of the men, weight of the ladder and tension supporting the ladder. Denotingmasses of men A,B,C and ladder by mA,mB,mCandmL, accelaration due to gravity by g, tension in the string by T and accelarations of the men A,B,C and ladder by aA,aB,ac and aL respectively, we can write the following equation according to equation.
Σ→F1=σ(m1→a1)→ T−mAg−mBg−mCg−mLg=mAaA+mBaB+mCaC+mLaL
Substituting given values of masses mA=40kg,mB=60kg,mC=50kg,mL=20kg, given values of accelarations g=10m/s2,aA=−2m/s2,aB=0m/s2,ac=1m/s2, and aL=0m/s2, we obtain T−400−600−500−200=−80+0+50+0
T=1670N
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-III
26 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-IV A
32 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
Similar Questions
Knowledge Check
Five equal resistances each of value R are connected in a form shown alongside. The equivalent resistance of the network
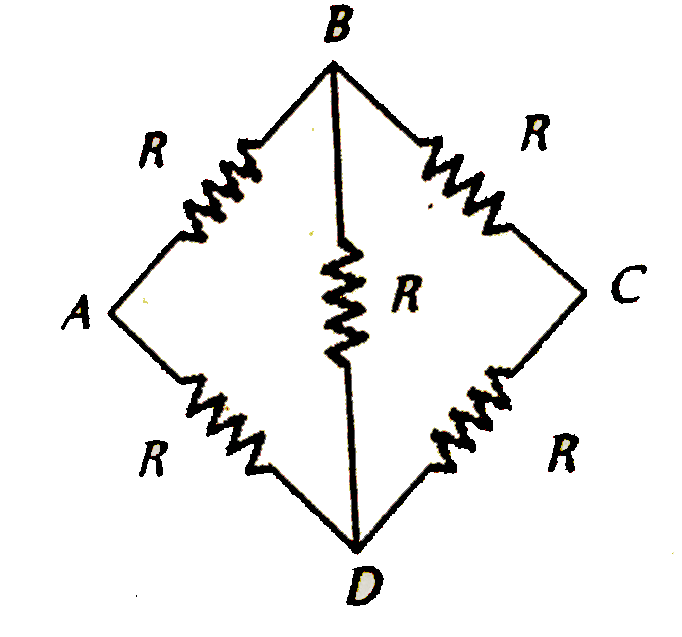 A12RB2RC58RD85R
A12RB2RC58RD85R
Two resistors of resistance R1 and R2 having R1>R2 are connected in parallel. For equivalent resistance R, the correct statement is
View SolutionTwo resistors of resistance R1 and R2 having R1>R2 are connected in parallel. For equivalent resistance R, the correct statement is
View SolutionFor two resistors R1 and R2, connected in parallel, find the relative error in their equivalent resistance. if R1=(50±2)Ω and R2=(100±3)Ω.
View SolutionResistance n, each of rohm, when connected in parallel give an equivalent resistance of Rohm. If these resistances were connected series, the combination would have a resistance in ohm, equal to
View SolutionA wire of resistance R is divided in 10 equal parts. These parts are connected in parallel, the equivalent resistance of such connection will be
View SolutionTwo cells of emfs ε1andε2 and internal resistances r1andr2 respectively are connected in parallel . Obtain expressions for the equivalent (i) resistance and , (ii) emf of the combination.
View SolutionResistances R1,R2,R3,R4,R5,andR6 are connected with a 6V battery with internal resistacne 1Ω as shown in fig 5.90. Find (a) equivalent resistance and (b) current in each resistacne.
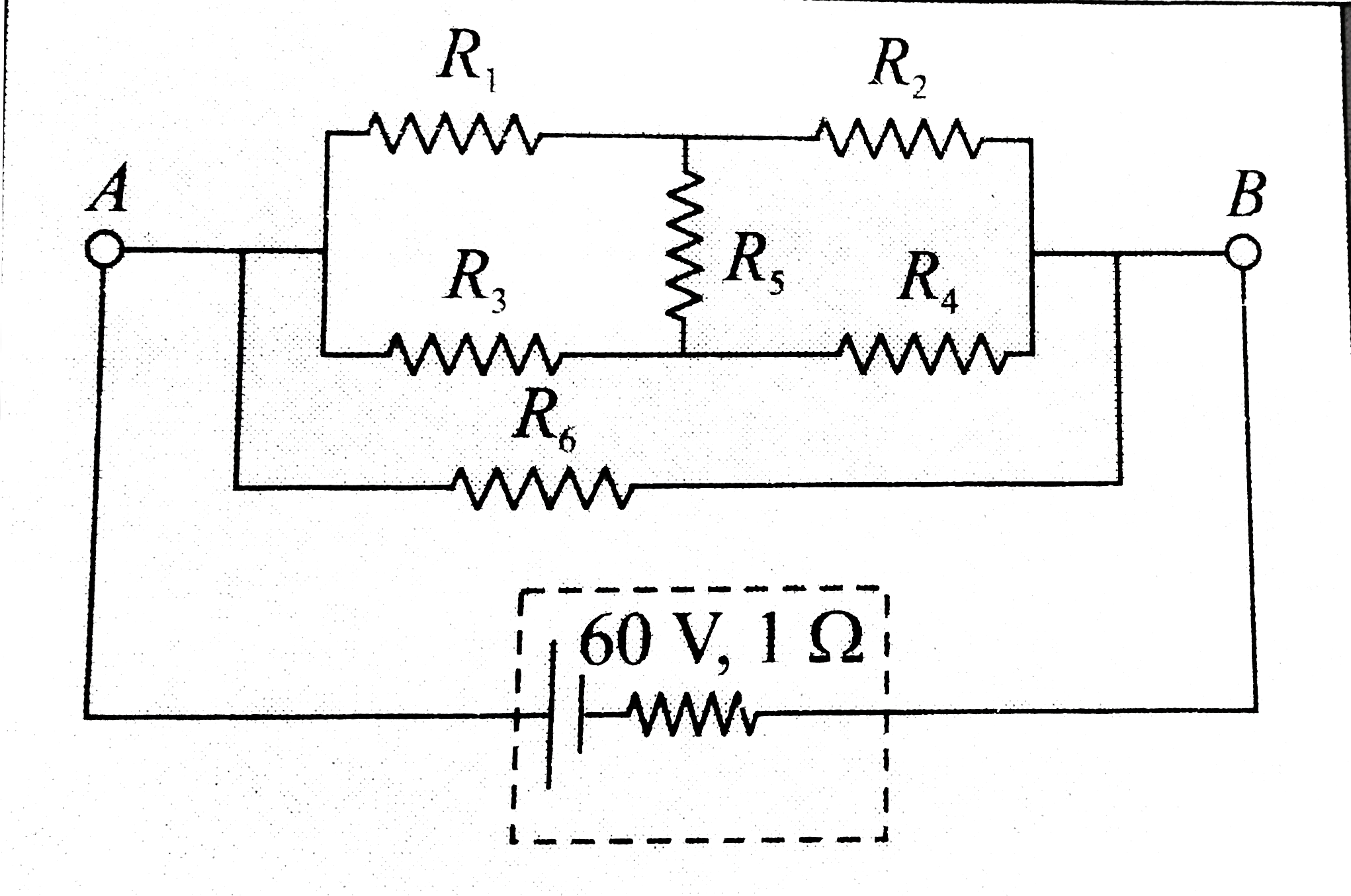
View Solution
