Resistance R,2R,4R,8R ...... ∞ are connected in parallel. What is their resutlant resistance will be
To find the resultant resistance of resistors R, 2R, 4R, 8R, ... connected in parallel, we can follow these steps:
1. Identify the Resistors: The resistors connected in parallel are R, 2R, 4R, 8R, and so on. This series continues infinitely.
2. Use the Formula for Parallel Resistance: The formula for the total (or resultant) resistance Rnet of resistors in parallel is given by:
1Rnet=1R1+1R2+1R3+…
In this case, we have:
1Rnet=1R+12R+14R+18R+…
3. Factor Out 1R: We can factor 1R out of the equation:
1Rnet=1R(1+12+14+18+…)
4. Recognize the Series as a Geometric Progression (GP): The series inside the parentheses is a geometric series where the first term a=1 and the common ratio r=12.
5. Sum of the Infinite Geometric Series: The sum S of an infinite geometric series can be calculated using the formula:
S=a1−r
Substituting the values:
S=11−12=112=2
6. Substituting Back to Find Rnet: Now substituting back into our equation for 1Rnet:
1Rnet=1R⋅2
Therefore,
Rnet=R2
Final Result:
The resultant resistance Rnet of the resistors R, 2R, 4R, 8R, ... connected in parallel is:
Rnet=R2
1Rnet=1R1+1R2+1R3+…
In this case, we have:
1Rnet=1R+12R+14R+18R+…
1Rnet=1R(1+12+14+18+…)
S=a1−r
Substituting the values:
S=11−12=112=2
1Rnet=1R⋅2
Therefore,
Rnet=R2
The resultant resistance Rnet of the resistors R, 2R, 4R, 8R, ... connected in parallel is:
Rnet=R2
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - SOLVED EXAMPLES
24 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE EXERCISE-1
5 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 48
1 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE
68 Videos
Similar Questions
The resistance 4R,16R,64R....∞ are connected in series. Find their equivalent resistance.
View Solution
Two batteries of E1 internal resistance r1 & emf E2 internal resistance r2 are connected in parallel and makes a battery system. An external resistance R is connected across this system as shown in the figure.
View SolutionResistance n, each of rohm, when connected in parallel give an equivalent resistance of Rohm. If these resistances were connected series, the combination would have a resistance in ohm, equal to
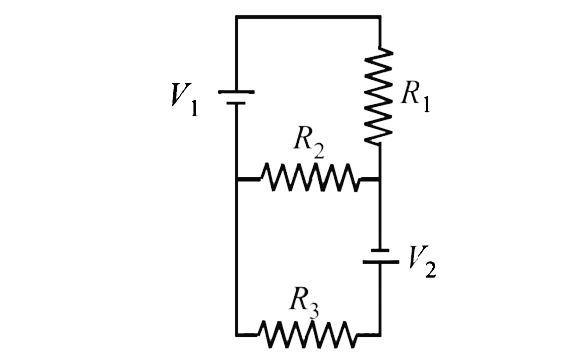
View SolutionTwo ideal batteries of emf V1andV2 and three resistances R1,R2andR3 are connected as shown in the figure. The current in resistance R2 would be zero if
View SolutionTwo resistors of resistance R1 and R2 having R1>R2 are connected in parallel. For equivalent resistance R, the correct statement is
View SolutionTwo resistors of resistance R1 and R2 having R1>R2 are connected in parallel. For equivalent resistance R, the correct statement is
View SolutionThree resistors R1,R2 and R3 are to be combined to form an electrical circuit as shown in the figure. It is found that when R1R2andR3 are put respectively in positions A, B and C, the effective resistance of the circuit is 70 ΩWhen R2,R3andR1 are put respectively in position A, B and C the effective resistance is 35Ω and when R3,R1andR2 are respectively put in the position A, B and C, the effective resistance is 42Ω
If R1,R2andR3 are all connected in parallel, the effective resistance will be
View SolutionFor two resistors R1 and R2, connected in parallel, find the relative error in their equivalent resistance. if R1=(50±2)Ω and R2=(100±3)Ω.
View SolutionThe resistance of a heater coil is 110Ω. A resistance R is connected in parallel with it and the combination is joined in series with a resistance of 11Ω to a 220V main line. The heater operates with a power of 110W. The value of R in Ω is
View SolutionLet there be n resistors R1...Rn with Rmax=max(R1....Rn) and Rmin=min{R1...Rn}. Show that when they are connected in parallel the resultant resistance Rp=Rmin and when they are connected in series, the resultant resistance RS>Rmax. Interpret the result physically.
View Solution
