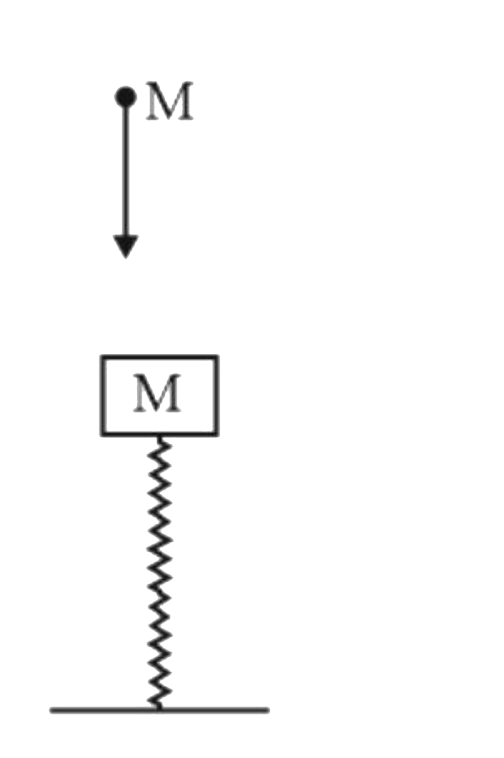
A mass M is in static equilibrium on a massless vertical spring as shown in the figure. A ball of mass m dropped from certain height sticks to the mass m after colliding with it. The oscillations they perform reach to height 'a' above the original level of spring & depth 'b' below it .

(a) Find the force constant of the spring.
(b) Find the oscillation frequency.
(c) What is the height above the initial level from which the mass m was dropped ?
The correct Answer is:A, B
(i) Let x0=Mgk = initial compression in spring
COME : 12k(x0+b)2=12k(a−x0)(2)+(m+M)g(b+a)
⇒k=2mgb−a
(ii) k=2mg(b−a)⇒(m+M)ω2=2mgb−a
⇒f=12π√2mg(b−a)(m+M)
(iii) Let h= initial height of m over the pan
v= common velocity of (m+M) after collision
COLM :m√(2gh)=(m+M)v......(i)
COME : 12kx02+12(m+M)v2+(m+M)gb=12k(x0+b)2
⇒=h=(M+mm)(abb−a)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise-05 [A]
Explore 39 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise-05 [B]
Explore 12 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise-04 [A]
Explore 20 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 24 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
Similar Questions
A mass M is in static equilibrium on a massless vertical spring as shown in the figure. A ball of mass m dropped from certain height sticks to the mass M after colliding with it.
The oscillations they perform reach to height'a' above the original level of scales & depth 'b' below it.
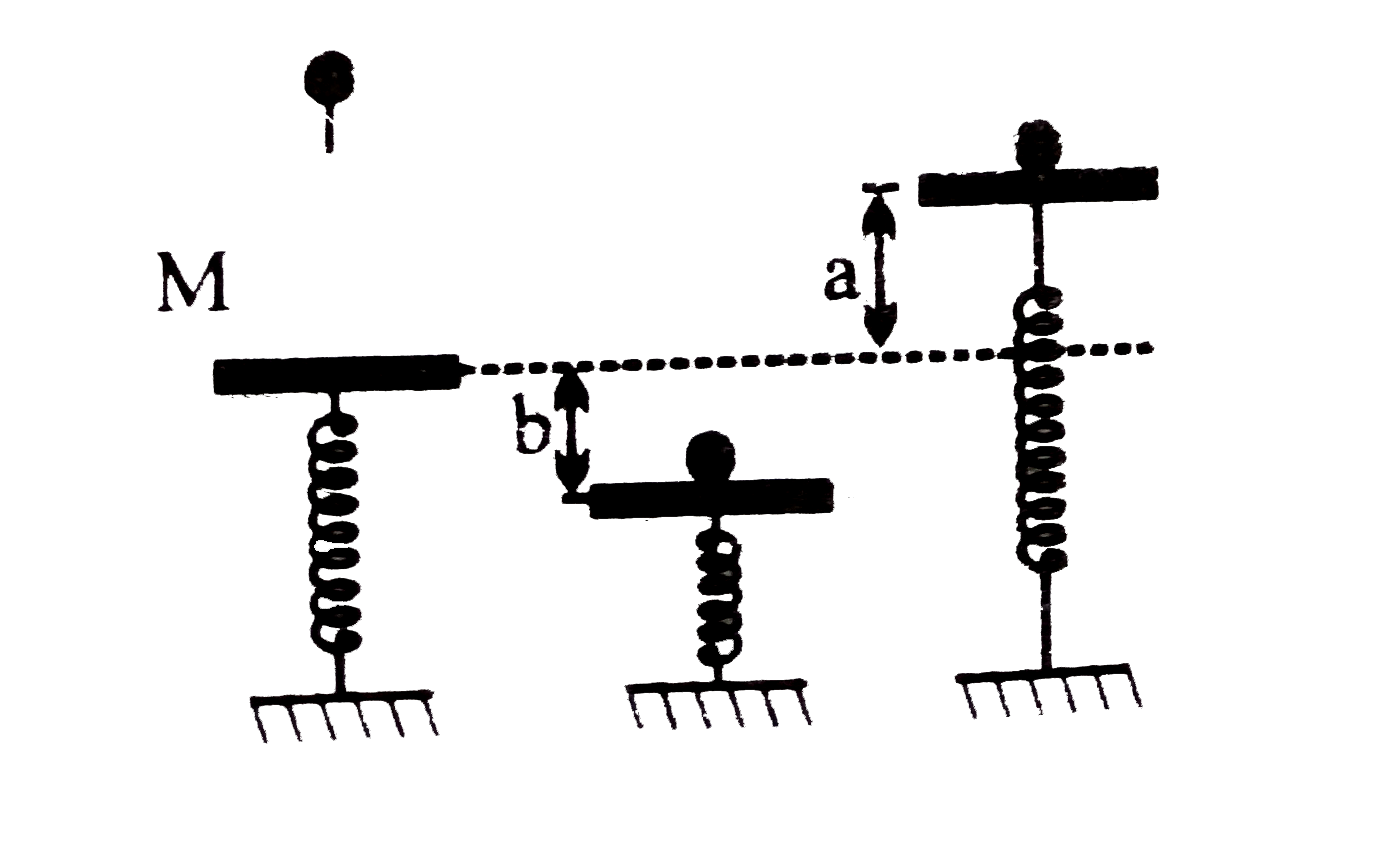
(a) Find the constant of force of the spring.,
(b) Find the oscillation frequency.
(c ) What is the height above the initial level from which the mass m was dropped?
View SolutionA mass M is in static equilibrium on a massless vertical spring as shown in the figure. A ball of mass m dropped from certain height sticks to the mass M after colliding with it.
The oscillations they perform reach to height'a' above the original level of scales & depth 'b' below it.
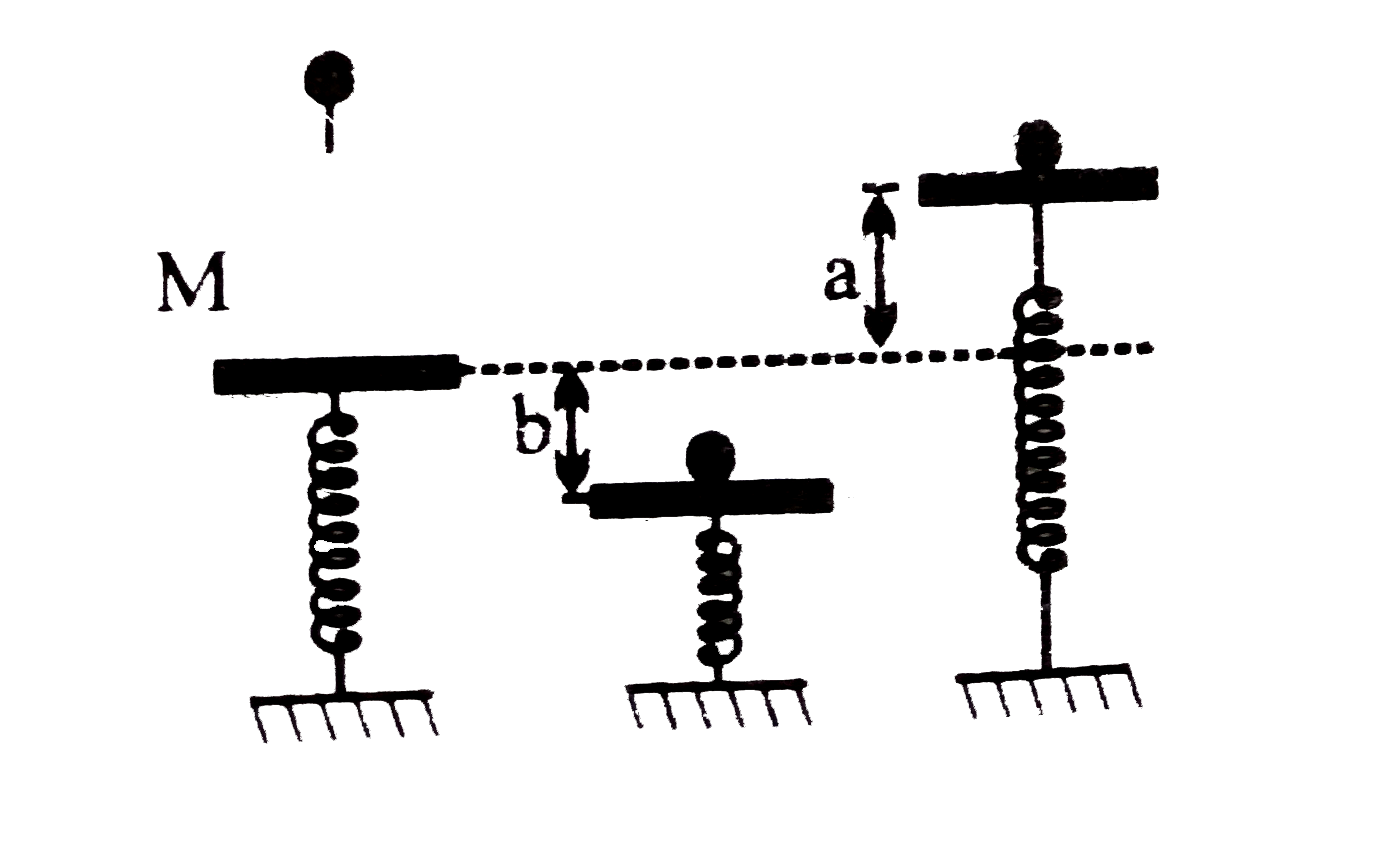
(a) Find the constant of force of the spring.,
(b) Find the oscillation frequency.
(c ) What is the height above the initial level from which the mass m was dropped?
View Solution
Knowledge Check
A massless platform is kept on a light elastic spring as shown in figure. When a small stone of mass 0.1 kg is dropped on the pan from a height of 0.24 m, the spring compresses by 0.01m. From what height should the stone be droppped to cause a compression of 0.04m in the spring ?
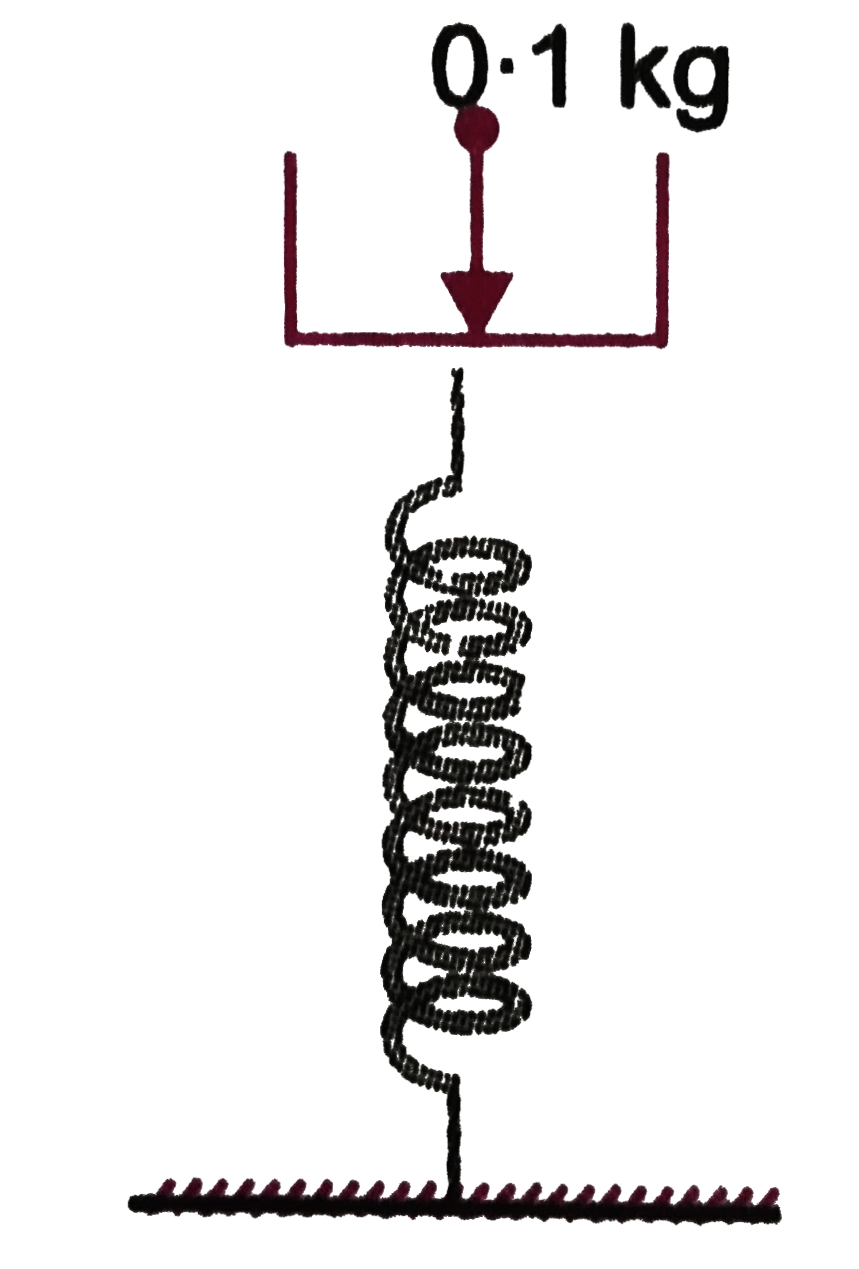 AA. 0.96 mBB. 2.96 mCC. 3.96 mDD. 0.48 m
AA. 0.96 mBB. 2.96 mCC. 3.96 mDD. 0.48 m
An ideal spring supports a disc of mass M. A body of mass m is released from a certain height from where it falls to hit M. The two masses stick together at the moment they touch and move together from then on . The oscillations reach to a height a above the original level of the disc and depth b blow. it The constant of the force of the spring is
View SolutionA body of mass m dropped from a certain height strikes a light vertical fixed spring of stifness k. the height of its fall before touching the spring the if the maximum compression of the spring the equal to 3mgk is
View Solution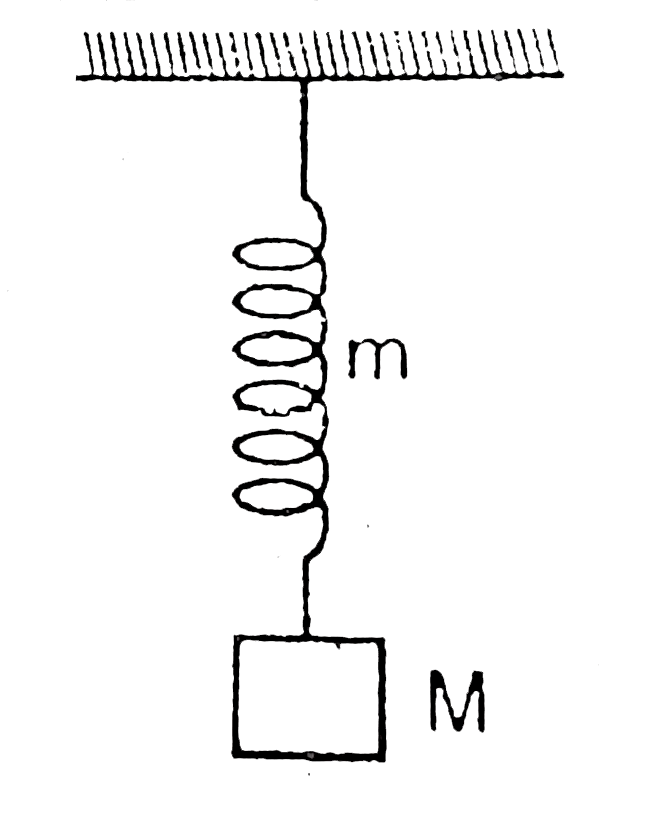
A block of M is suspended from a vertical spring of mass m as shown in the figure. When block is pulled down and released the mass oscillates with maximum velocity v.
View SolutionA rod mass (M) hinged at (O) is kept in equilibrium with a spring of stiffness (k) as shown in figure. The potential energy stored in the spring is .

View SolutionA ball of mass 'm' drops from a height which sticks to a massless hanger after striking it. Neglecting overturning. Find out the maximum extension in rod, assuming that the rod is massless.
View SolutionA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View SolutionA ball of mass m is droppped from a height h on a platform fixed at the top of a vertical spring. The platform is depressed by a distance x. What is the spring constant K?
View Solution
