A mass M is in static equilibrium on a massless vertical spring as shown in the figure. A ball of mass m dropped from certain height sticks to the mass M after colliding with it.
The oscillations they perform reach to height'a' above the original level of scales & depth 'b' below it.
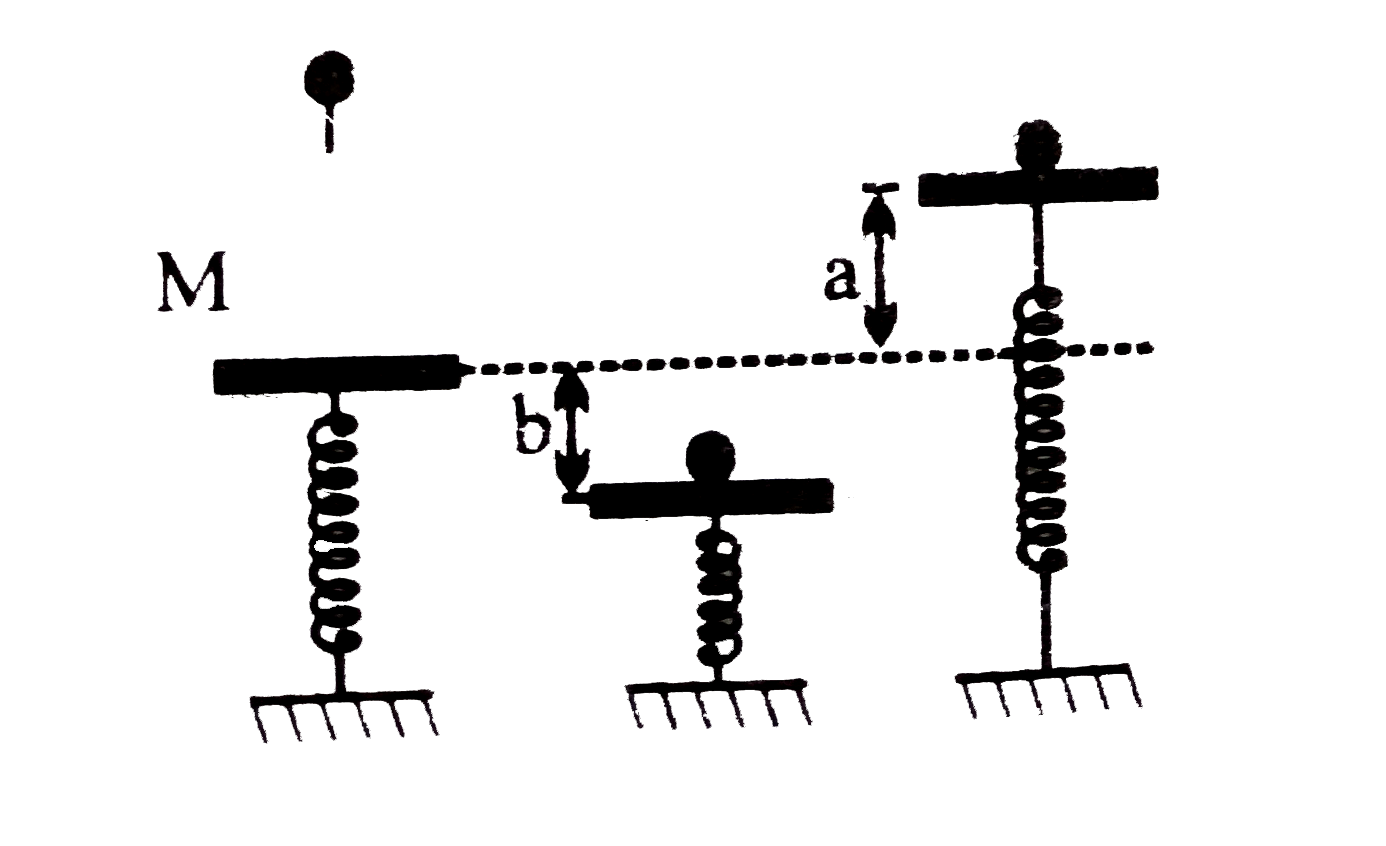
(a) Find the constant of force of the spring.,
(b) Find the oscillation frequency.
(c ) What is the height above the initial level from which the mass m was dropped?
The correct Answer is:A, B, C
Ans:(a)K=2mgb−a
(b)12π√kM+m
(c)(M+mb−a)abm

Amplitude =b−mgK=a+mgK( by diagram )
⇒K=2mgb−a
(b)f=1T=12π√MK+m
(c) If the ball was fropped from 'h'.
⇒Vbefore collision=√2gh
conserving momentum :
m√2gh=(m+M)V' Where V'
=ω√A2−x2=√KM+m√(b−mgK)2−(mgK)2
Squaring both sides and putting
K=2mgb−a,get h=(M+mb−a)abm.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 75
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 76
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp73
Explore 4 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 53 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCE ENGLISHChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
An ideal spring supports a disc of mass M. A body of mass m is released from a certain height from where it falls to hit M. The two masses stick together at the moment they touch and move together from then on . The oscillations reach to a height a above the original level of the disc and depth b blow. it The constant of the force of the spring is
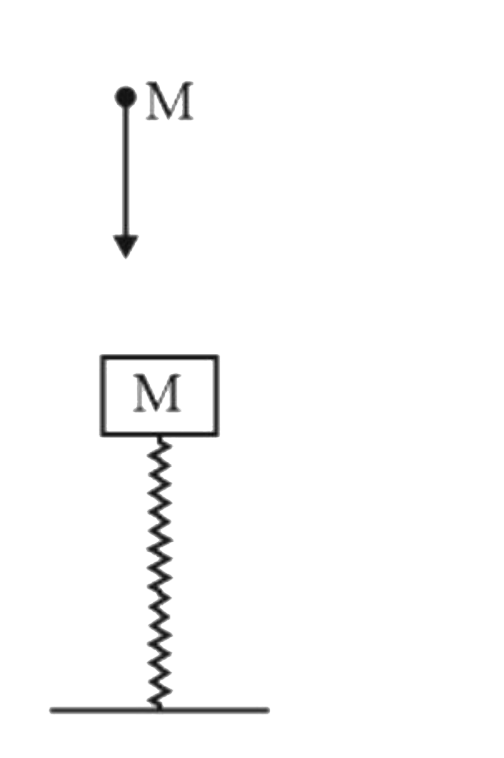
View SolutionA ball of mass m is droppped from a height h on a platform fixed at the top of a vertical spring. The platform is depressed by a distance x. What is the spring constant K?
View SolutionA ball of mass 'm' drops from a height which sticks to a massless hanger after striking it. Neglecting overturning. Find out the maximum extension in rod, assuming that the rod is massless.
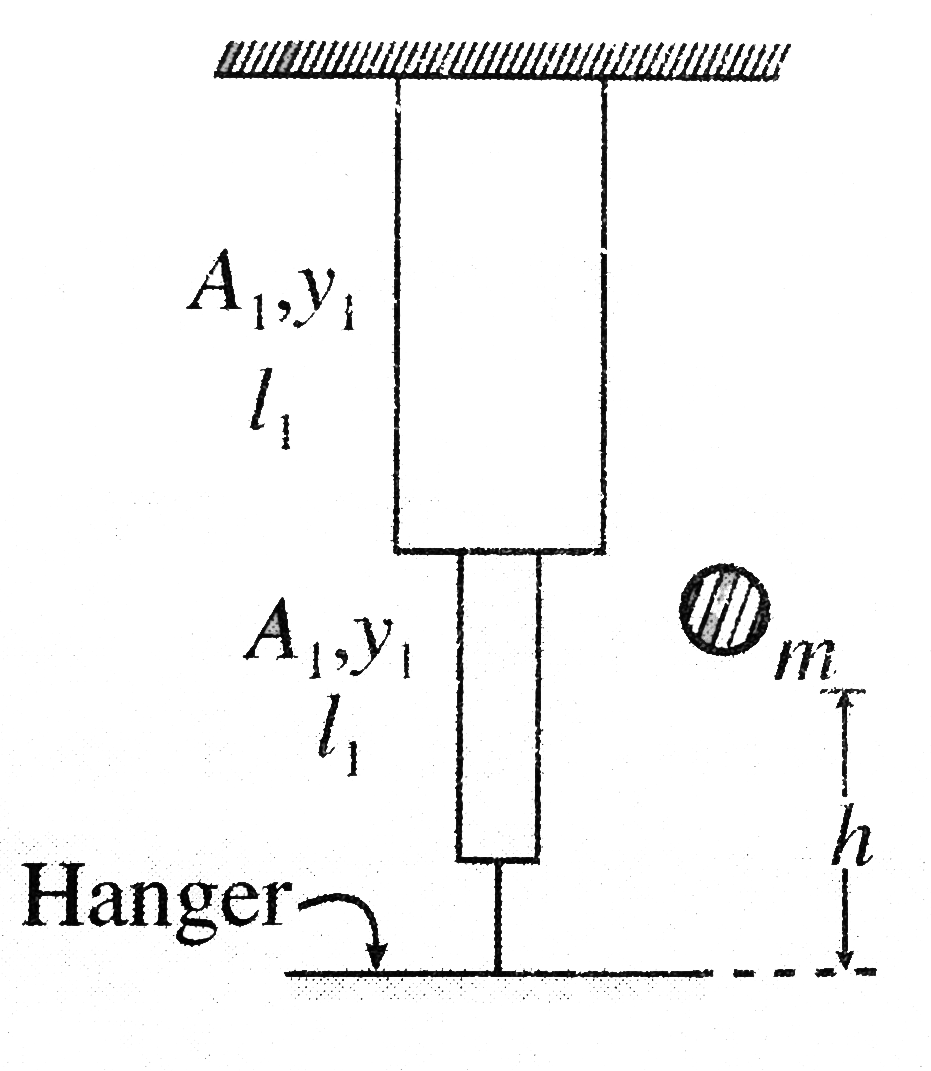
View SolutionA body of mass m dropped from a certain height strikes a light vertical fixed spring of stifness k. the height of its fall before touching the spring the if the maximum compression of the spring the equal to 3mgk is
View Solution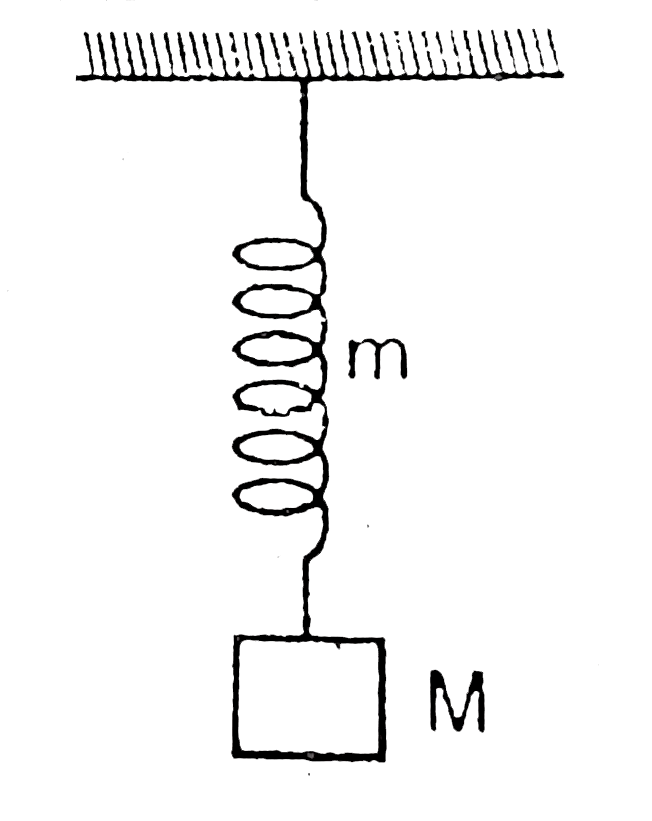
A block of M is suspended from a vertical spring of mass m as shown in the figure. When block is pulled down and released the mass oscillates with maximum velocity v.
View SolutionA ball of mass 'm' drops from a height which sticks to a mass-less hanger after striking it. Neglecting overturning, Find out the maximum extension in rod, assuming that the rod is mass-less.
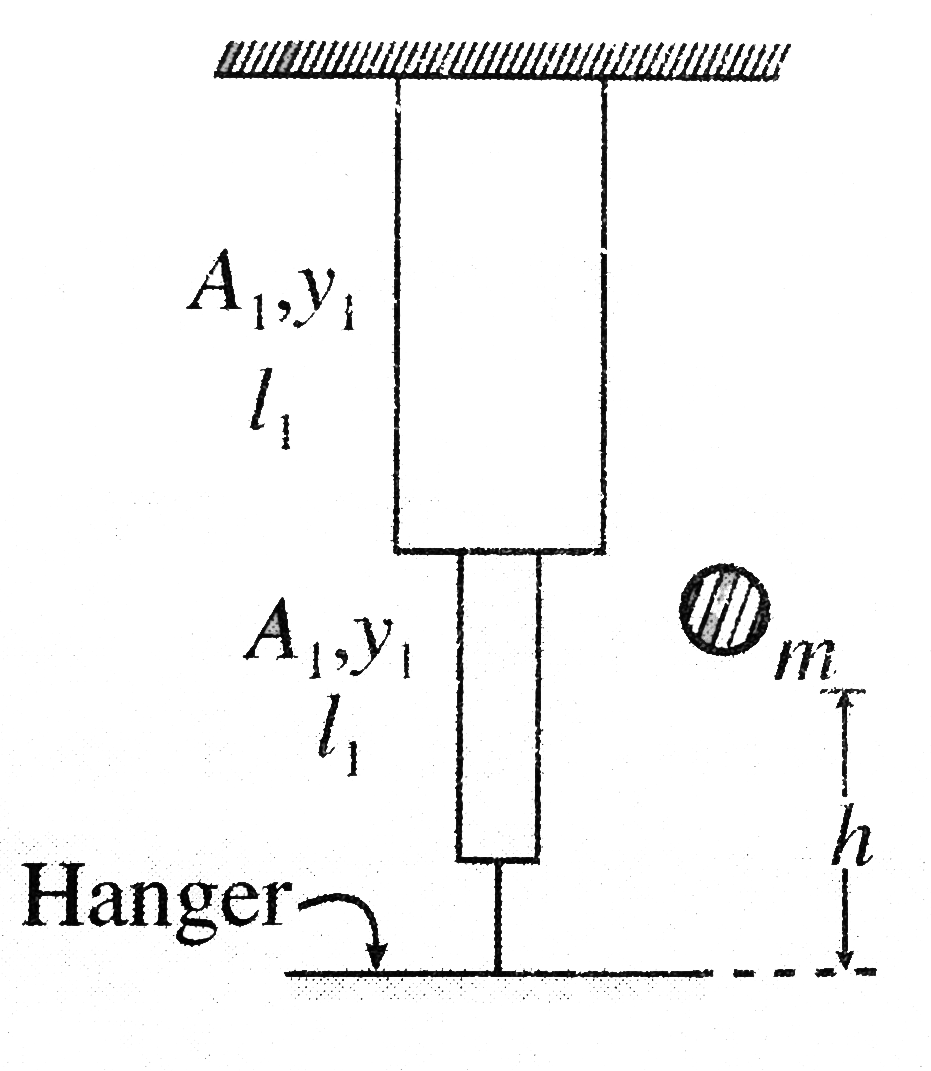
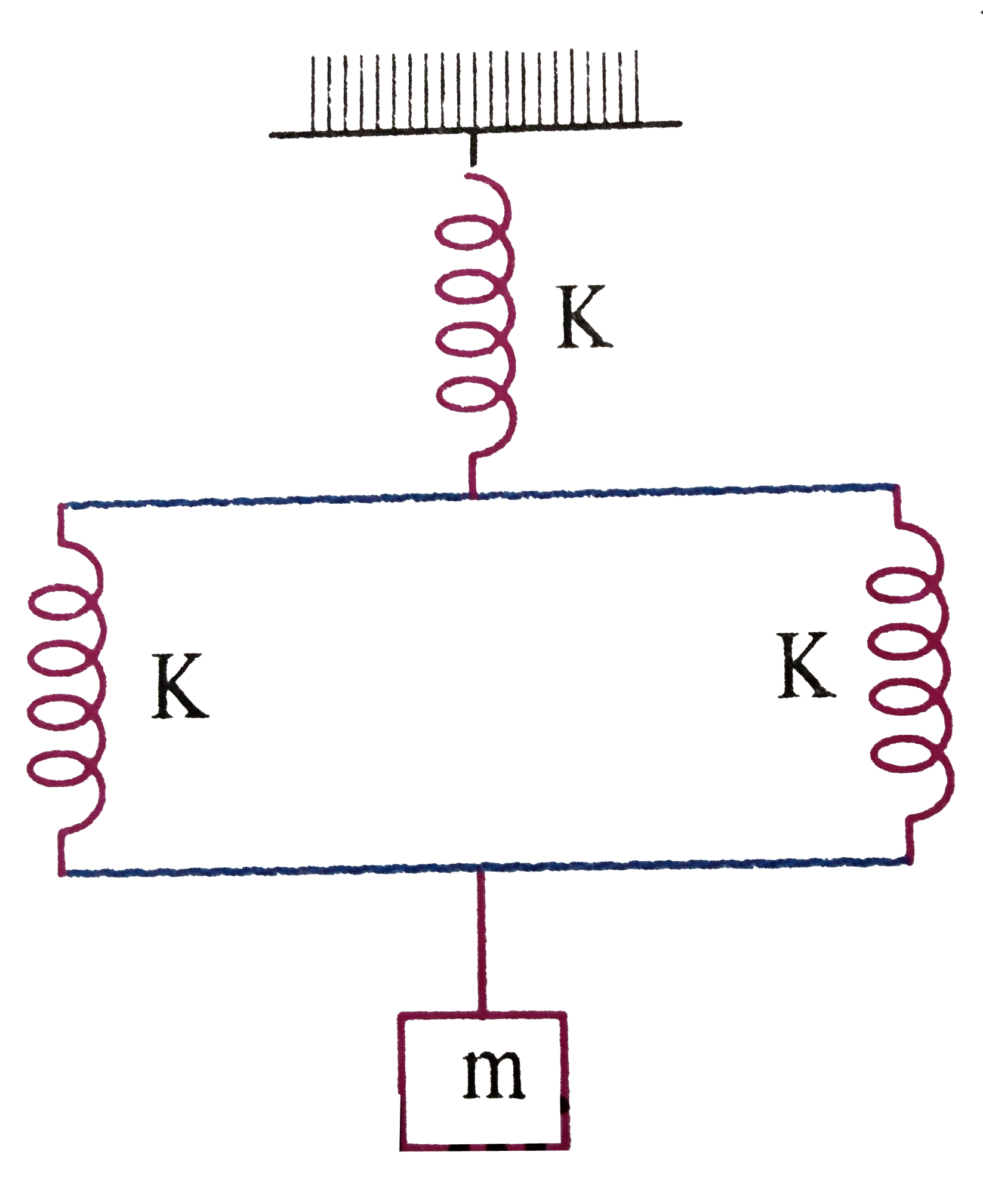
View SolutionA body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is
View SolutionSystem shown in fig is in equilibrium and at rest. The spring and string are massless now the string is cut. The acceleration of mass 2m and m just after the string is cut will be:

View SolutionSystem shown in fig is in equilibrium and at rest. The spring and string are massless now the string is cut. The acceleration of mass 2m and m just after the string is cut will be:

View SolutionA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View Solution