In the arrangement shown in figure, pulleys are light and spring are ideal. K1, k2, k3and k4 are force constant of the spring. Calculate period of small vertical oscillations of block of mass m.

The correct Answer is:A, B, C, D
Let block be displacement by x than displacement in springs be
x1,x2,x3 and x4
Such that x=2x1+2x2+2x3+2x4
Now let restoring force on m be F=kx then
2f=k1x1=k2x2=k3x3=k4x4
⇒Fk=4Fk1+4Fk2+4Fk3+4Fk4
⇒1k=4(1k1+1k2+1k3+1k4)
T=2π√mk=2π√4m(1k1+1k2+1k3+1k4)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [A]
39 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [B]
12 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-04 [A]
20 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
24 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
In the arrangement shown in the diagram, pulleys are small and springs are ideal. k1=k2=k3=k4=10Nm−1 are force constants of the springs and mass m=10kg. If the time period of small vertical oscillations of the block of mass m is given by 2πx seconds, then find the value of x.
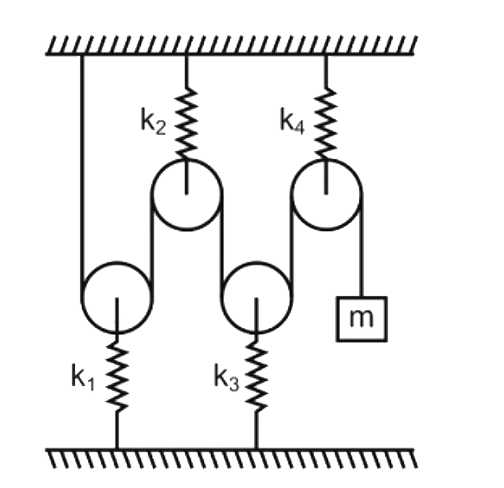
View Solution
In the arrangement shown if Fig. Pulleys are small and lught and spring are ideal and K1=25(π2)Nm, K2=2K1,K3= and K4=4K1 are the force constant of the spring. Calculate the period of small vertical oscillation of block of mass m=3kg.
View SolutionIn the situation as shown in figure time period of small vertical oscillation of block will be - (String, springs and pulley are ideal)
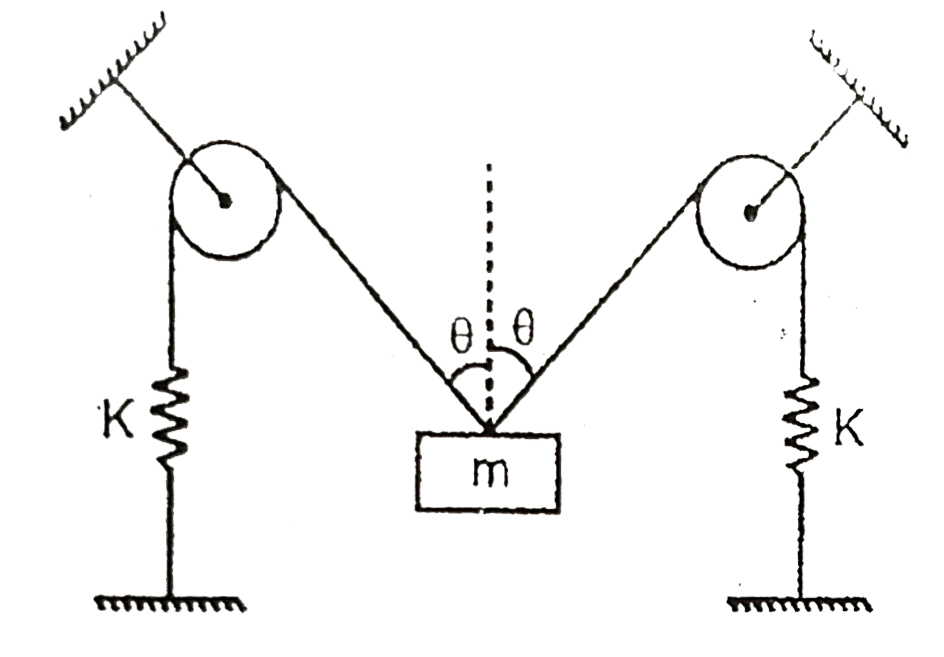
View SolutionAs shown in the figure, two light springs of force constant k1 and k2 oscillate a block of mass m. Its effective force constant will be
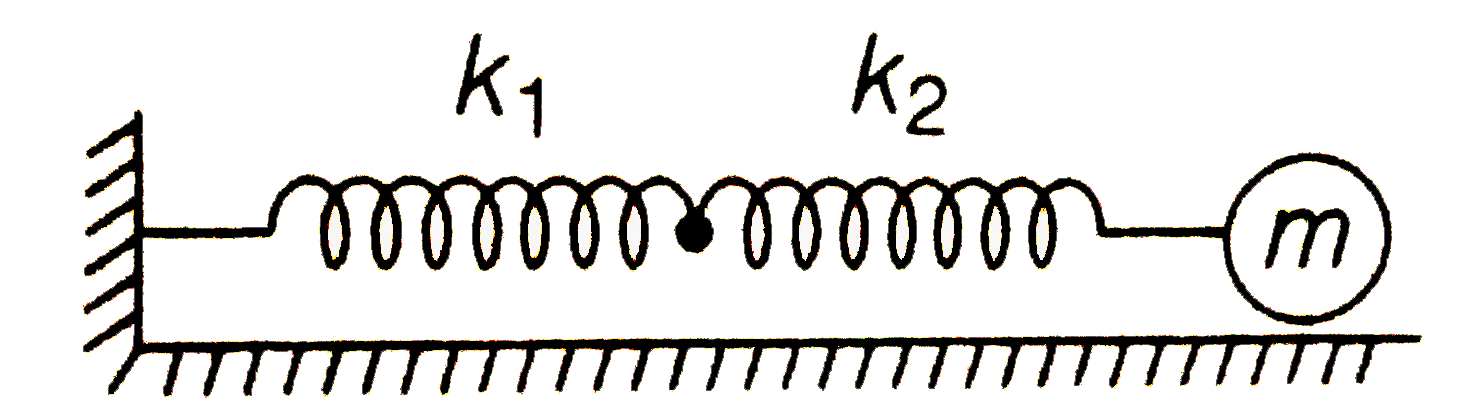
View SolutionTwo light spring of force constants k1 and k2 and a block of mass m are in one line AB on a smooth horizontal table such that one end of each spring is fixed on rigid supports and the other end is free as shown in the figure. The distance CD between the spring is 60cm. If the block moves along AB with a velocity 120cm/s in between the springs, calculate the period of oscillation of the block. (take k1=1.8N/m, k2=3.2N/m, m=200g)

View Solution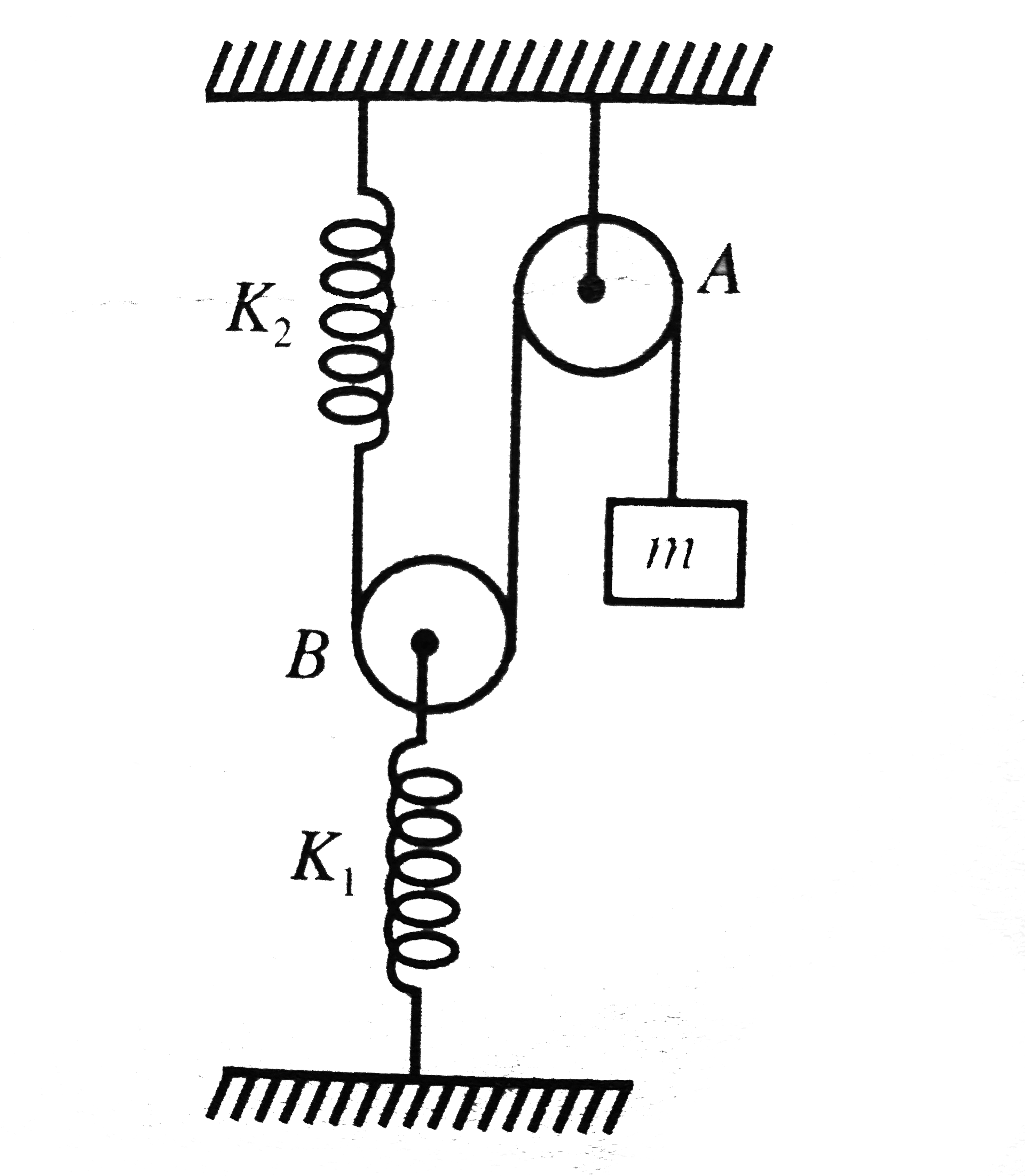
A block of mass m is tied to one end of a spring which passes over a smooth fixed pulley A and under a light smooth movable pulley B. The other end of the string is attached to the lower end of a spring of spring constant K2. Find the period of small oscillation of mass m about its equilibrium position (in second). (Take m=π2kg,K2k=4K1,K1=17Nm.)
View SolutionA block of mass m is attached to one end of a light inextensible string passing over a smooth light pulley B and under another smooth light pulley A as shown in the figure. The other end of the string is fixed to a ceiling. A and B are held by spring of spring constants k1 and k2. Find angular frequency of small oscillations of small oscillations of the system.

View SolutionThe is an arrangement of pulleys as shown in figure. All the pulley are massless and frcitionless and the strings used are inextensible. Each of these springs have a spring constant k. We define the stiffness of the assembly k1 as the force required to be applied at point A for its unit displacement.
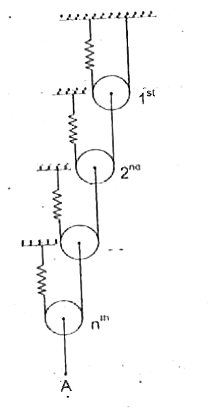
What will he the most probable value of k1 for n =3
View SolutionThe is an arrangement of pulleys as shown in figure. All the pulley are massless and frcitionless and the strings used are inextensible. Each of these springs have a spring constant k. We define the stiffness of the assembly k1 as the force required to be applied at point A for its unit displacement.
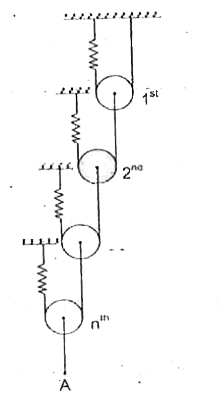
Find k1 for n=2
View SolutionThe is an arrangement of pulleys as shown in figure. All the pulley are massless and frcitionless and the strings used are inextensible. Each of these springs have a spring constant k. We define the stiffness of the assembly k1 as the force required to be applied at point A for its unit displacement.
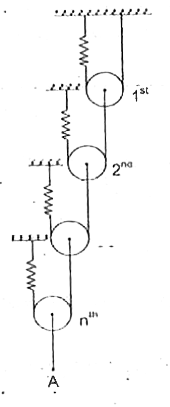
Find k1 for n = 1
View Solution
