A rod of mass M and length K is hinged at its one end n carris a block f mass m at its other end. A spring of force constant k1 is installed at distance a form the hinge and another of force constant k2 at a distance b as shown in the figure. If the whole arrangement rests on a smoth horizontal table top. Find the frequency of vibrations.
_E01_120_Q01.png)
The correct Answer is:A, B, C
_E01_120_S01.png)
For small angular displacement θ, net torque towards mean position is
τ=(k1aθ)a+(k2bθ)b⇒Iα=(k1a2+K2b2)θ
⇒(mL2+13ML2)α=(k1a2+k2b2)θ
⇒α=k1a2+k2b2L2(m+M3)θ∴ω2=k1a2+k2b2L2(m+M3)
Hence frequency
f=ω2π=12π
⎷k1a2−k2b2L2(m+M3)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise-05 [A]
Explore 39 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise-05 [B]
Explore 12 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise-04 [A]
Explore 20 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 24 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
Similar Questions
A rod of mass M and length L is hinged at its one end and carries a particle of mass m at its lower end. A spring of force constant k1 is installed at distance a from the hinge and another of force constant k2 at B distance b as shown in the figure. If the whcich arrangement rests on a smoth horizontal table top, the frequency of vibration is :
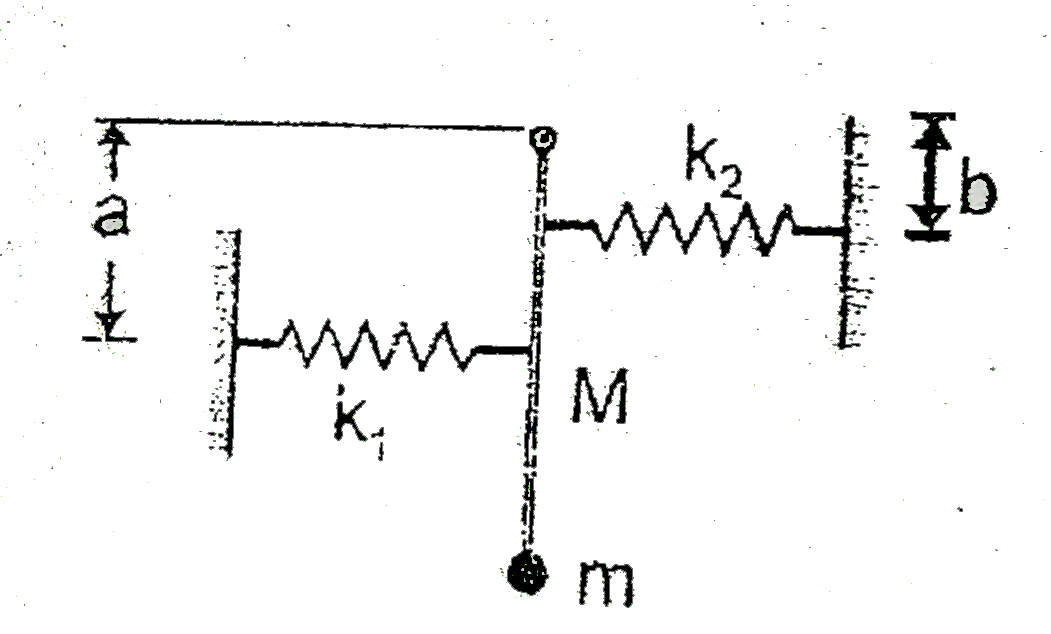
View SolutionA rod of mass m and length l is hinged at one of its end A as shown in figure. A force F is applied at a distance x from A. The acceleration of centre of mass a varies with x as

View SolutionA rod of mass m and length l is hinged at one of its ends A as shown in figure. A force F is applied at a distance x from A . The acceleration of centre of mass varies with x as −
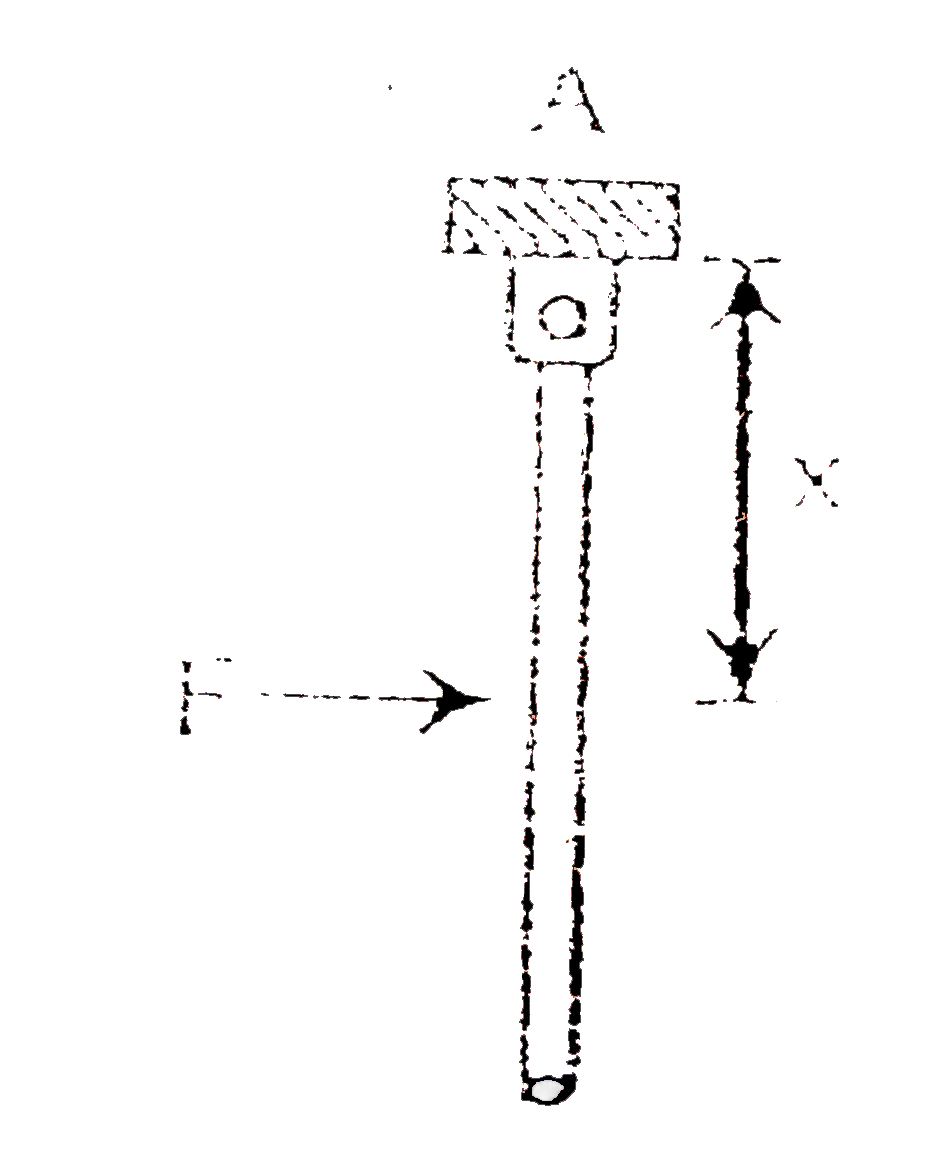
View SolutionA rod of mass m and length l is hinged at one of its ends A as shown in figure. A force F is applied at a distance x from A . The acceleration of centre of mass varies with x as −
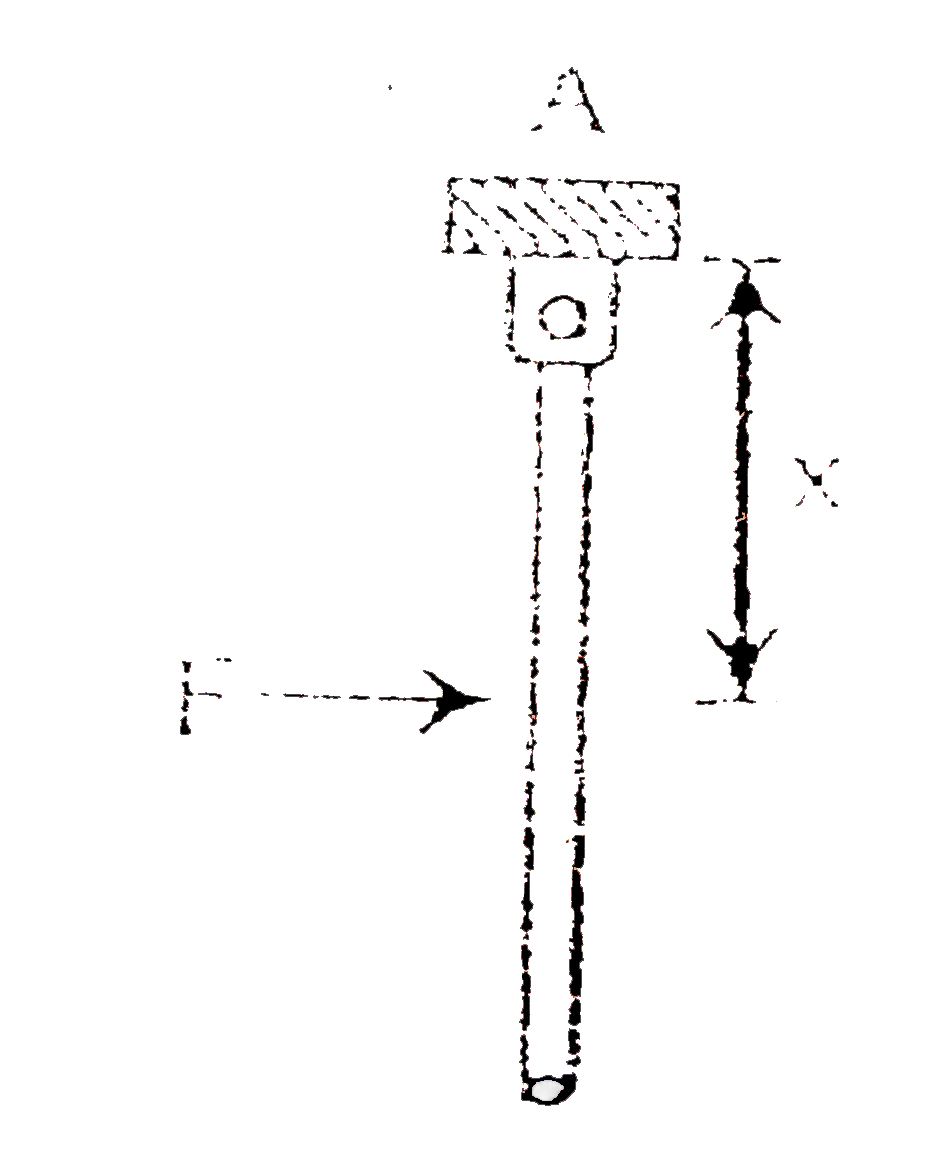
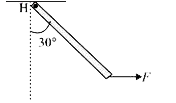
View SolutionA rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:
View SolutionAs shown in the figure, two light springs of force constant k1 and k2 oscillate a block of mass m. Its effective force constant will be
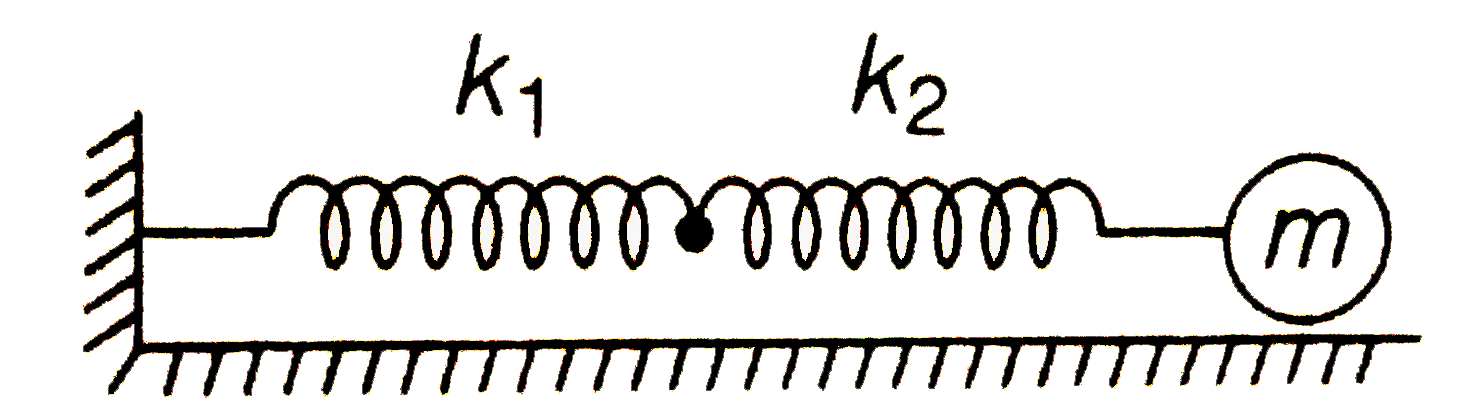
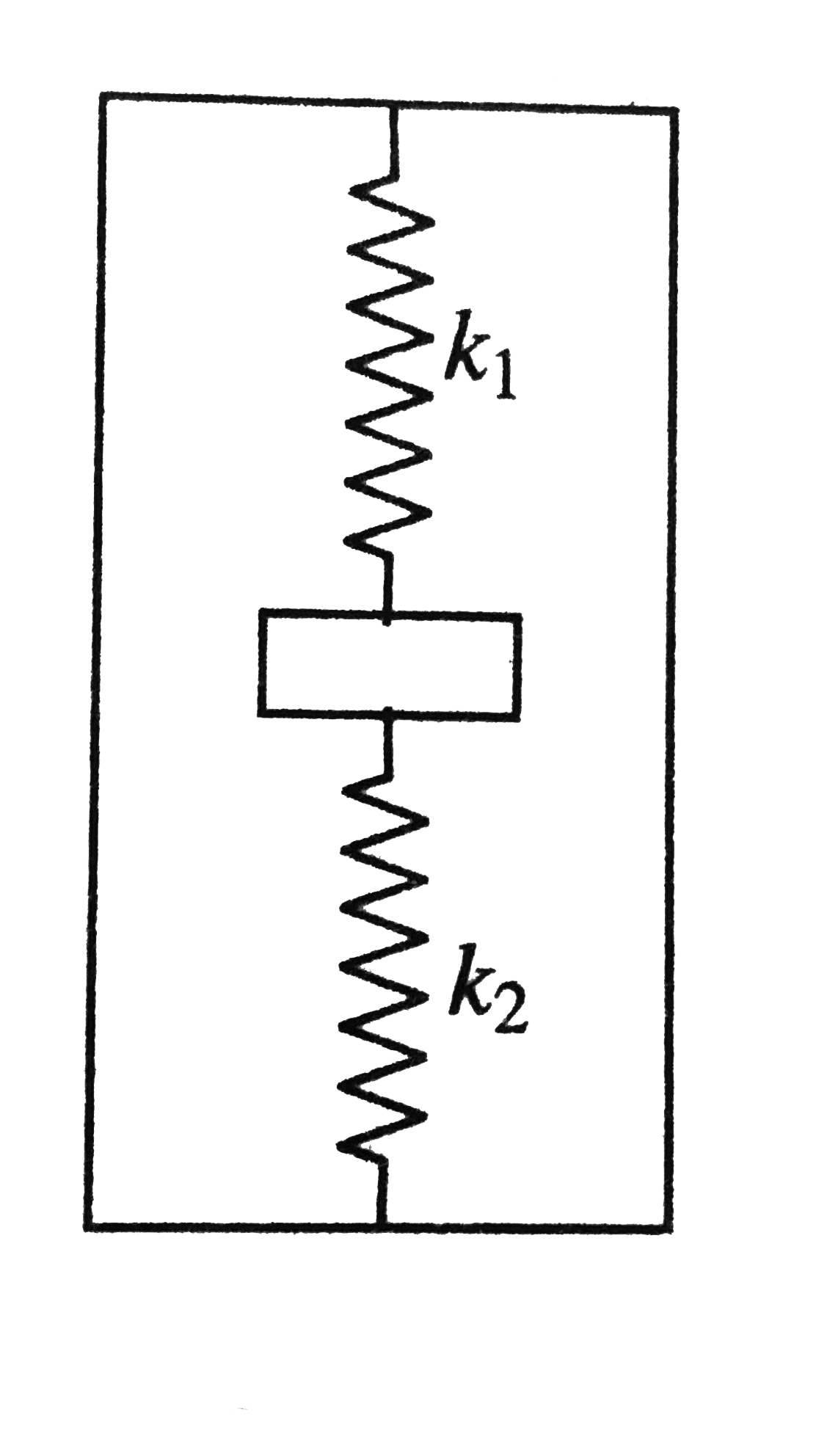
View SolutionOne end of a spring of force constant k1 is attached to the ceiling of an elevator. A block of mass 1.5kg is attached to the other end. Another spring of force constant k2 is attached to the bottom of the mass and to the floor of the elevator as shown in figure. At equilibrium, the deformation in both the spring is equal and is 40cm. If the elevator moves with constant acceleration upward, the additional deformation in both the spring is 8cm. Find the elevator's accelerationn ( g=10ms−2).
View SolutionA rod AB of mass M and length L is shown in figure. End A of rod is hinged and end B is lying on the ground. Find the Horizontal component of the force applied by the hinge

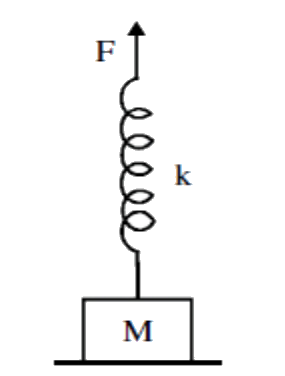
View SolutionA block of mass m is kept on a rough horizontal surface and is attached with a massless spring of force constant k. The minimum constant force applied on the other end of the spring of lift the block is
View Solution
A horizontal rod of mass m and length L is pivoted at one end The rod's other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released. The angular frequency of the subsequent simple harmonic motion is
View Solution

