The two torsion pendula differ only by the addition of cylindrical masses as shown in the figure. The radius of each additional mass is 1/4 the radius fo the disc. Each cylinder and disc have equal mass. The ratio of time periods of the two torsion pendula is p. Then 27p2 is.
_E01_110_Q01.png)
I1=MR22
I2=[M2(R4)2+M(3R4)2]+[M2(R4)2+M(3R4)2]+MR22
T∝√1
T1T2∝√I1I2
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-04 [B]
105 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [A]
39 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension Base Questions (5)
3 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
24 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
Two blocks each having a mass M are placed as shown in the figure. The accleration of the system is:-

View SolutionFind the position of center of mass of the uniform lamina shown in figure, if small disc of radius α2 is cut from disc of radius a.
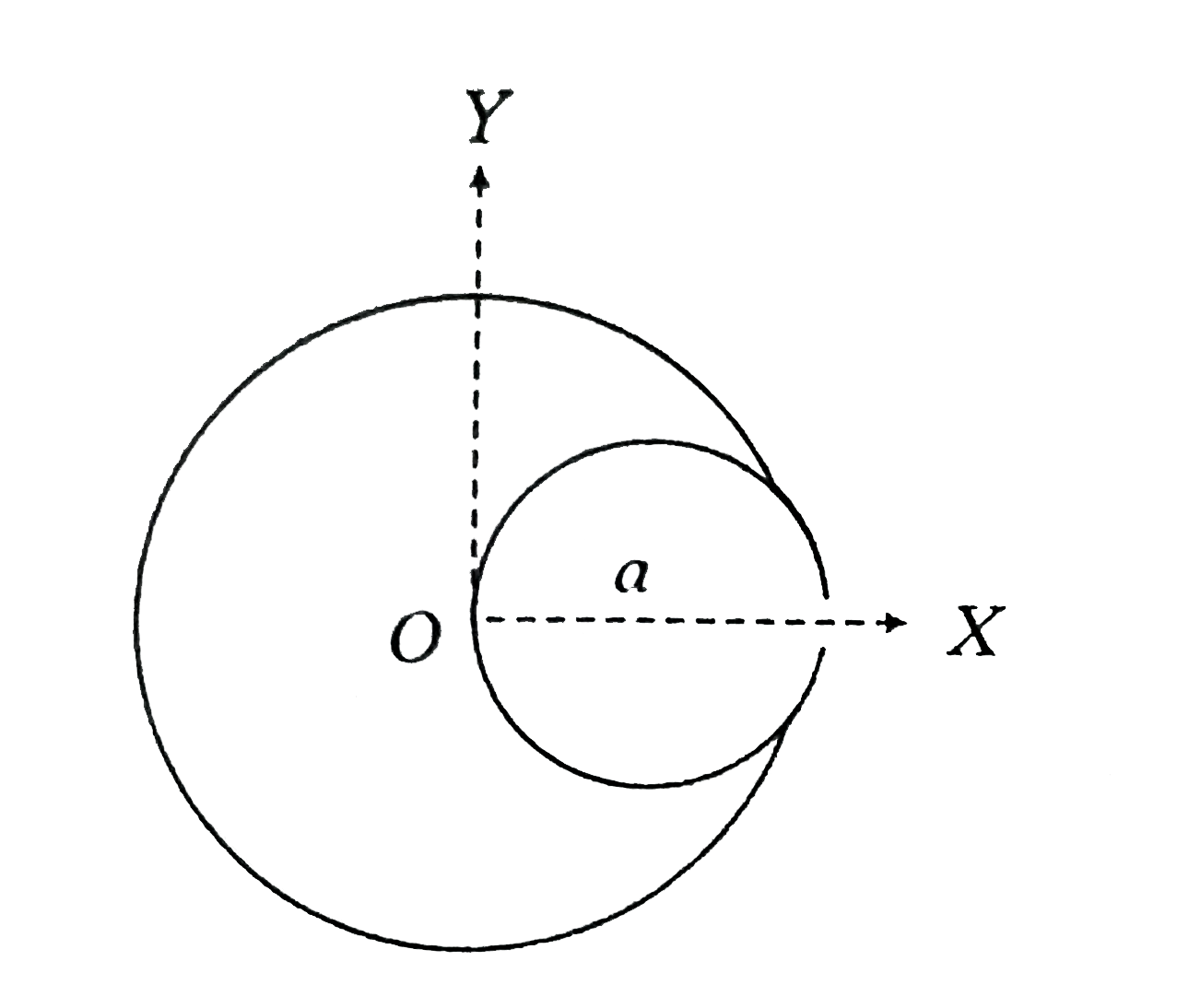
View Solution
Two identical discs of mass m and of radius R touch each other and move with the same velocity perpendicularly to the line segment which joins their centres of mass, along the surface of a horizontal smooth tabletop. There is a third disc of mass M and of radius R at rest, at a point on thhe perpendicular bisector of of the line segment joining the centres of mass of the two moving discs as shown in the figure. The two moving discs collide elastically with the third one, which is at rest there is no friction between the rims of the discs. What should the ratio of M/m be in order that after the collision the two discs of mass m move perpendicularly to their intial velocity?
View SolutionThe ratio of the radii of gyration of a circular disc to that of a circular ring, each of same mass and radius, around their respective axes is.
View SolutionTwo identical uniform discs of mass m and radius r are arranged as shown in the figure. If α is the angular acceleration of the lower disc and acm is acceleration of centre of mass of the lower disc, then relation among acm,α and r is
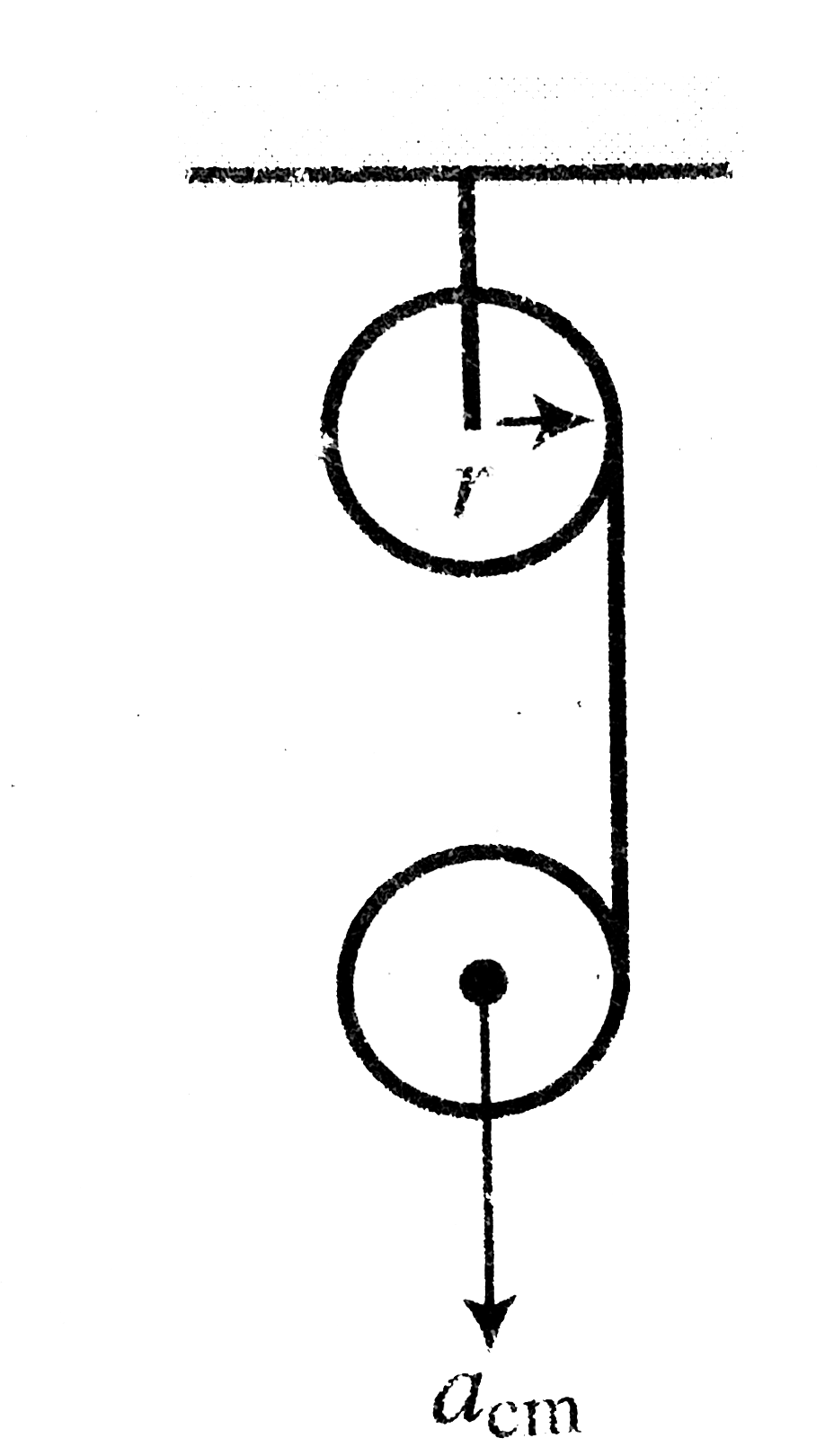
View SolutionThree forces of magnitude F, F and √2F are acting on the periphery of a disc of mass m and radius R as shown in the figure. The net torque about the centre of the disc is
View SolutionA disc of mass m and radius R is rolling without slipping as shown in the figure. The magnitude of net velocity of the point P is (OP=R2)
View SolutionThree rings, each of mass P and radius Q are arranged as shown in the figure. The moment of inertia of the arrangement about YY' axis will be

View SolutionA disc of mass 1 kg and radius 10 cm is suspended by vertical wire at its centre. If the time period is 3.2 s. Find the modulus of torison.
View SolutionA hollow hemisphere of mass 4m is placed as shown in figure . Two point masses m each are fixed to it at points P and Q on diametrically opposite points. The position of center of mass of the system is
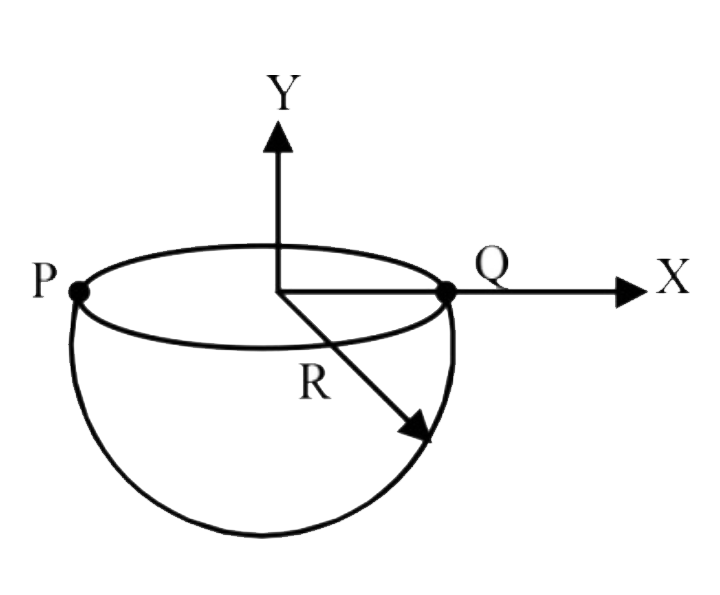
View Solution
