A small ring of mass m1 is connected by a string of length l to a small heavy bob of mass m2. The ring os free to move (slide) along a fixed smooth horizontal wire. The bob is given a small displacement from its equilibrium position at right angles to string. Find period of small oscillations.
_E01_106_Q01.png)
The correct Answer is:A, B
Centre of mass will be at rest as there is no external
So effective length
leff=(m1m1+m2)l
t=2π√leffg=2π√m1l(m1+m2)g
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-04 [B]105videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [A]39videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension Base Questions (5)3videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)24videos
RACE
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
A small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.
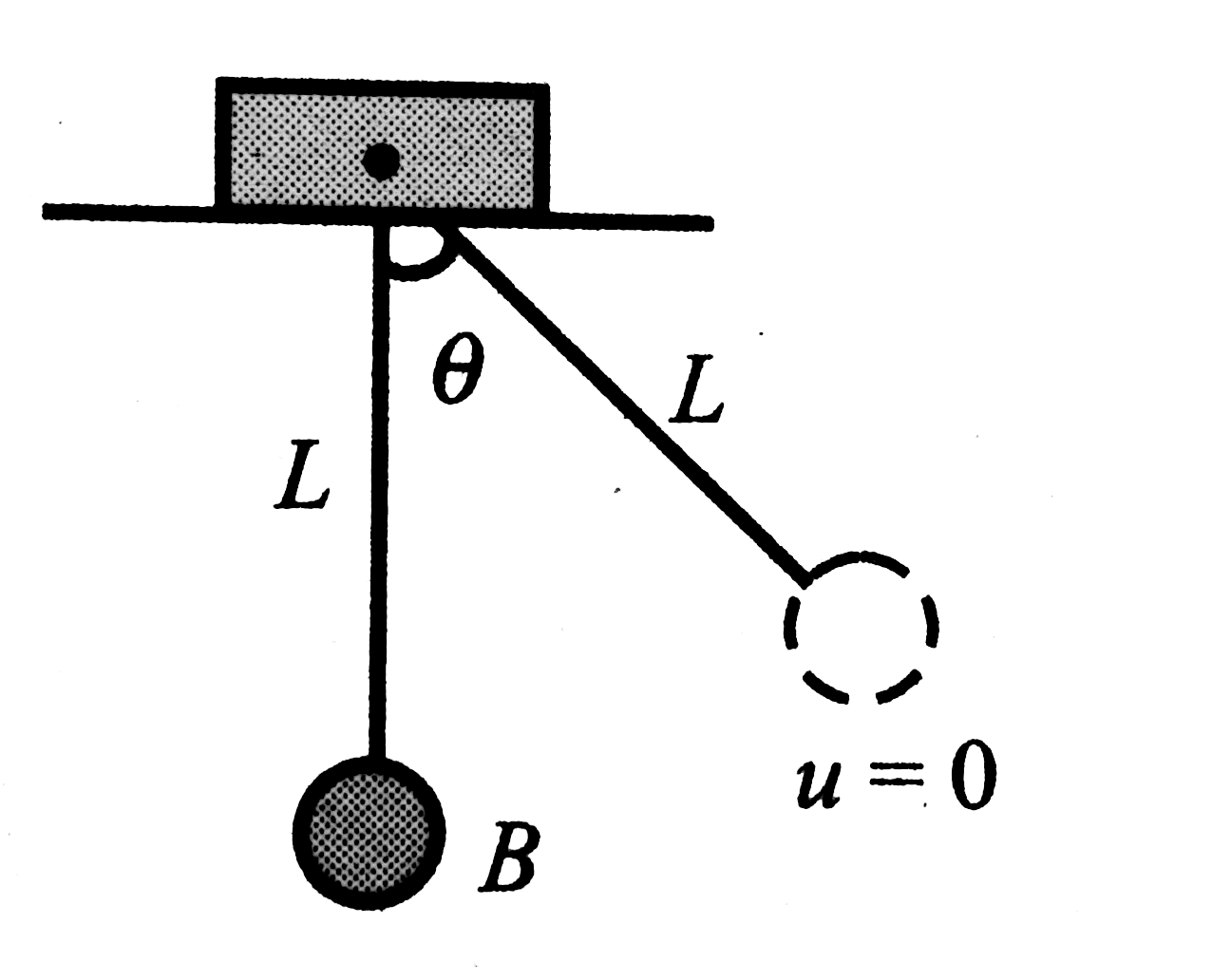
Tension in string when it is vertical, isView SolutionA small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.
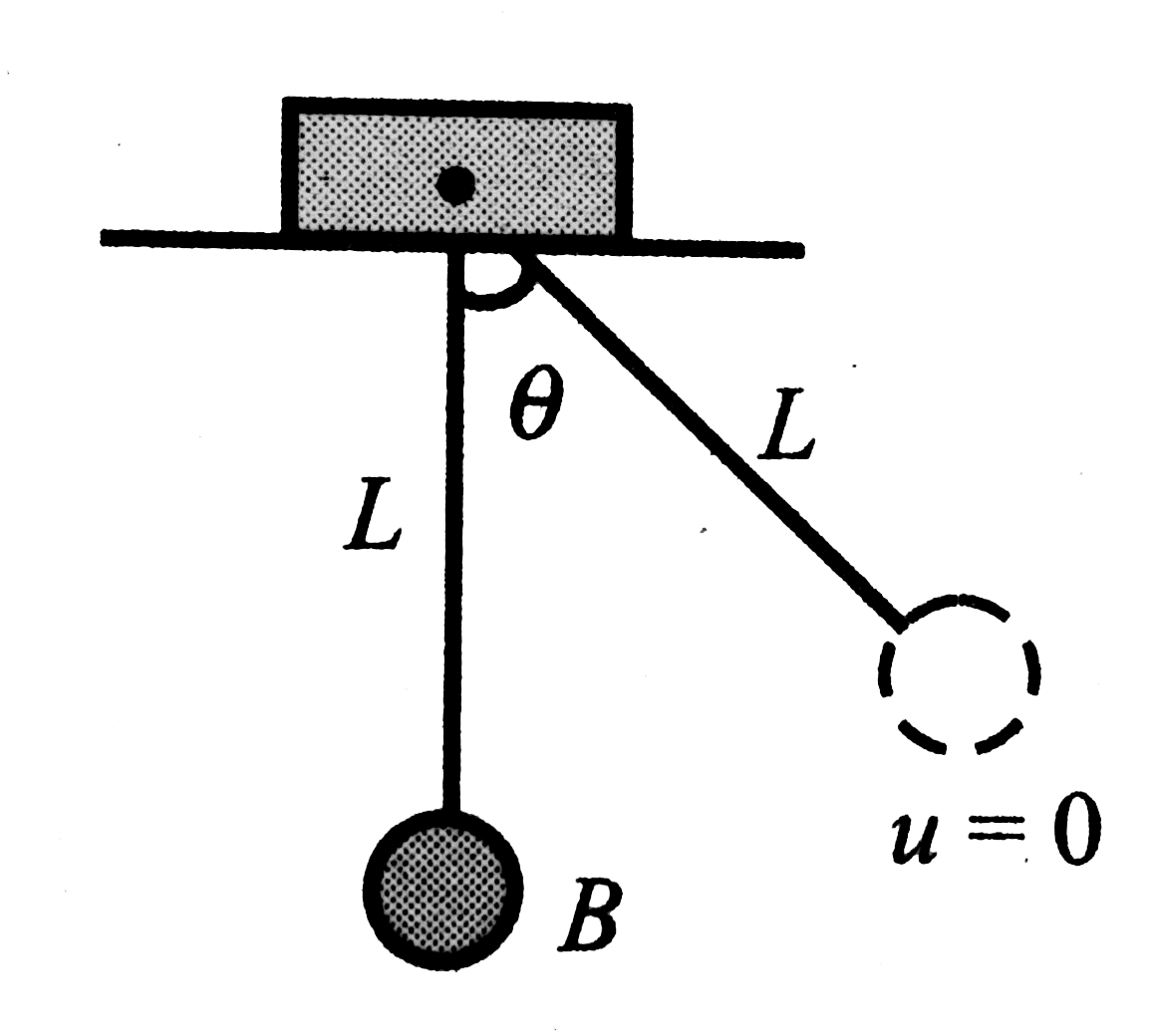The displacement of centre of mass of A+B system till the string becomes vertical is View SolutionA small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.
The displacement of block when equilibrium position isView SolutionA block of mass m slides down on a wedge of mass M as shown in figure .Let a1 be the asseleration of the acceleration of and a2 the the acceleration od block 1N1 is the normal reaction between block and wedge and N2 the normal reaction between wedge and gound .frication is absent everwhere .Select the correct alternative(s)
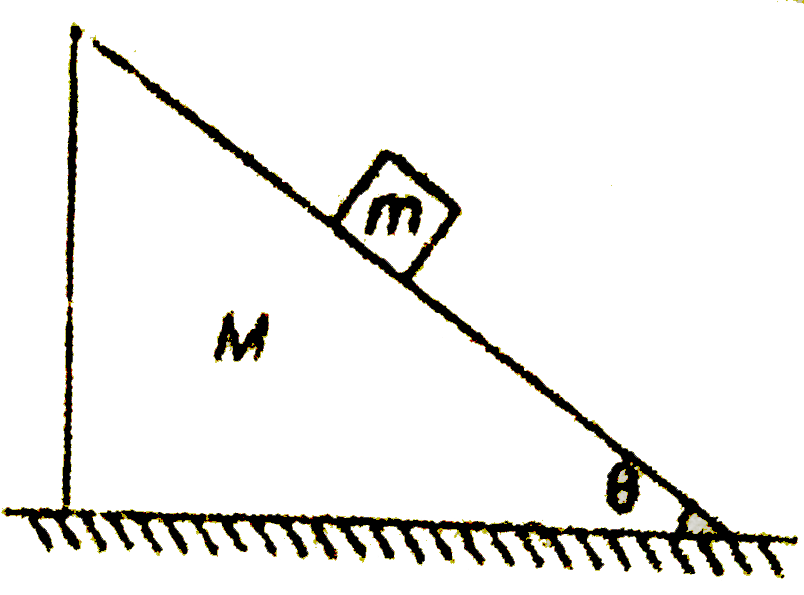
View SolutionA system consisting of a smooth movable wedge of angle α and a block A of mass m are connected together with a massless spring of spring constant k, as shown in the figure. The system is kept on a frictionless horizontal plane. If the block is displaced slighlly from equilibrium and left to oscillate, find the frequency of small oscillations.
View SolutionA ring of mass m and radius a is connected to an inextensible string which passes over a frictionless pulley. The other end of string is connected to upper end of a massless spring of spring constant k. The lower end of the spring is fixed. The ring can rotate in the vertical plane about hinge without any friction. If horizontal position of ring is equilibrium position then find time period of small in oscillations of the ring.
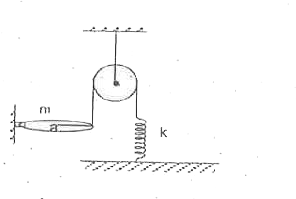
View SolutionThere is a rod of length l and mass m. It is hinged at one end to the ceiling. The period of small oscillation is
View SolutionA particle of mass 2m is connected by an inextensible string of length 1.2m to a ring of mass m which is free to slide on a horizontal smooth rod. Initially the ring and the particle are at the same level with the string taut. Both are then released simultaneously. The distance in meter moved by the ring when the string becomes veritcal is :-
View SolutionTwo light strings, each of length l are fixed at points A andB on a fixed horizontal and xy A small are making angle 45∘ with the bob if the bob is displaced normal to the plane of the string and released then period of the resulting small oscillation will be
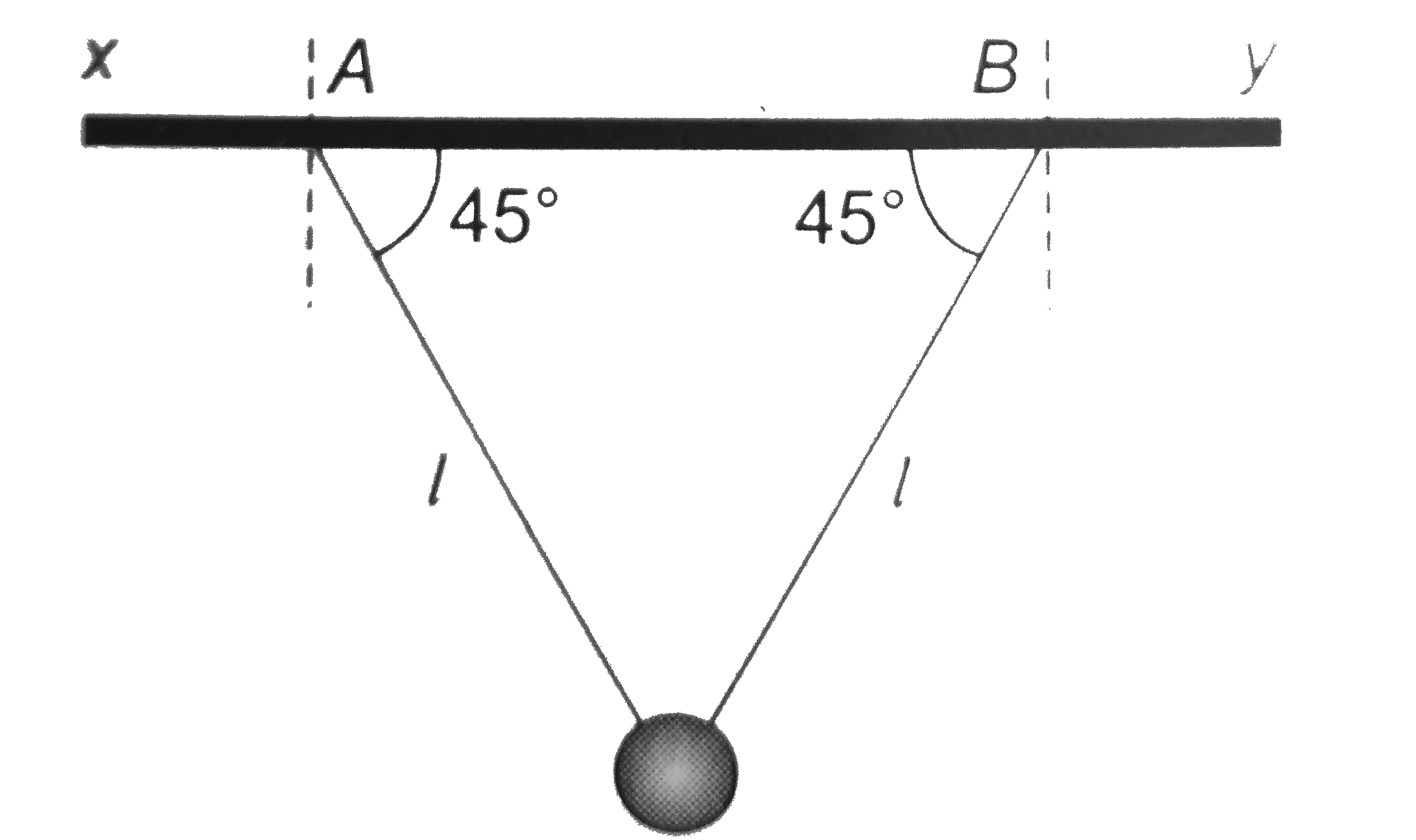
View SolutionA spherical bob of mass m and radius R is attached to a fixed point by means of a massless rigid rod whose length from the point of support up to the centre of bob is l. Find the period of small oscillation.
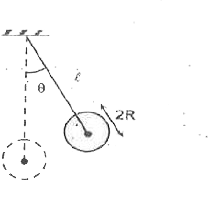
View Solution