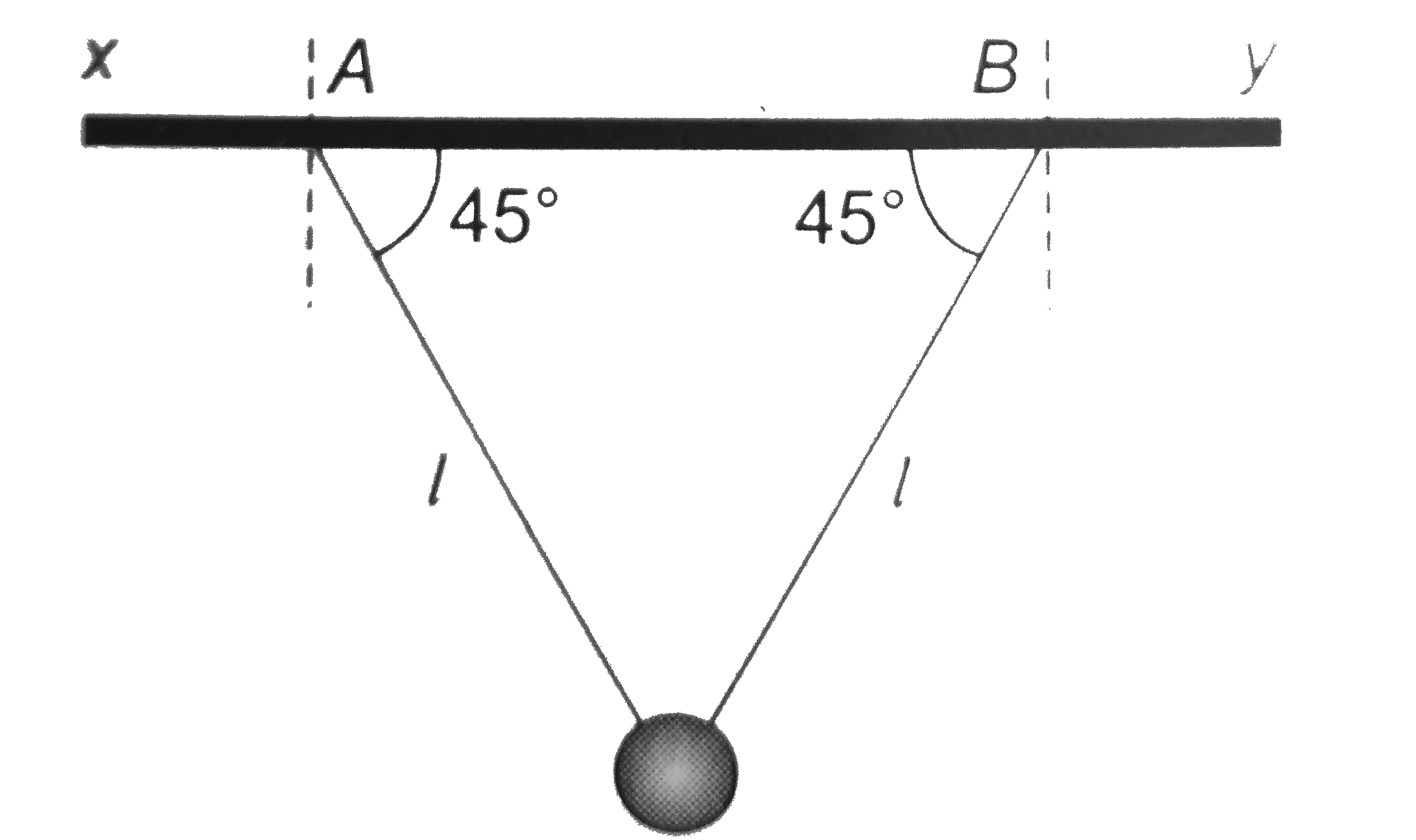
Two light strings, each of length l are fixed at points A andB on a fixed horizontal and xy A small are making angle 45∘ with the bob if the bob is displaced normal to the plane of the string and released then period of the resulting small oscillation will be
2π√2√2lg
2π√√2lg
2π√lg
2π√l√2g
The correct Answer is:D
Resulting torque on the bob =mgl√2sinθ
Ml of bob about axis xy=ml22
For small angle θ=mgl√2sinθ
α=τI=√2glθ
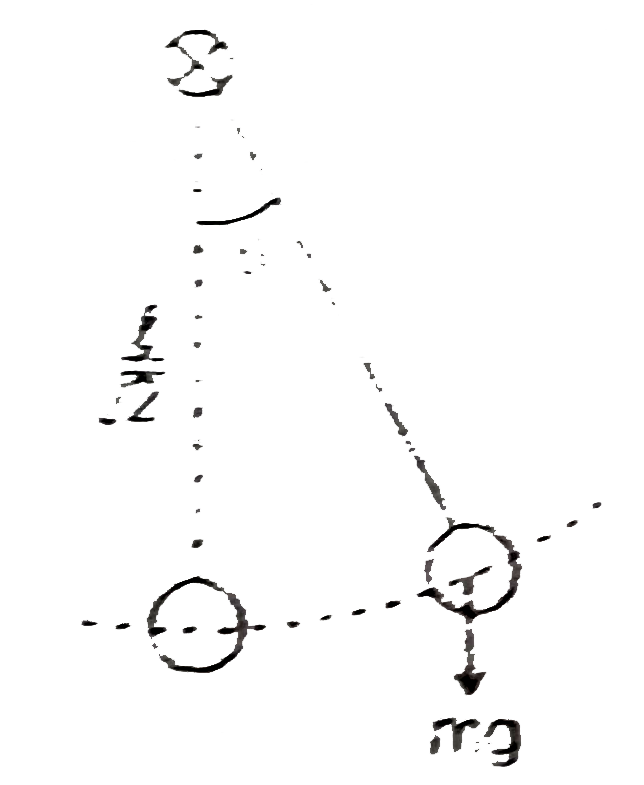
ω=√√2gk⇒T=2π√l√2g.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.71
10 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.72
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.69
20 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
Time period of small oscillation (in a verical plane normal to the plane of strings) of the bob in the arrangement shown will be
_E01_023_Q01.png)
View SolutionTwo identical rods each of mass m and length L, are tigidly joined and then suspended in a vertical plane so as to oscillate freely about an axis normal to the plane of paper passing through 'S' (point of supension). Find the time period of such small oscillations
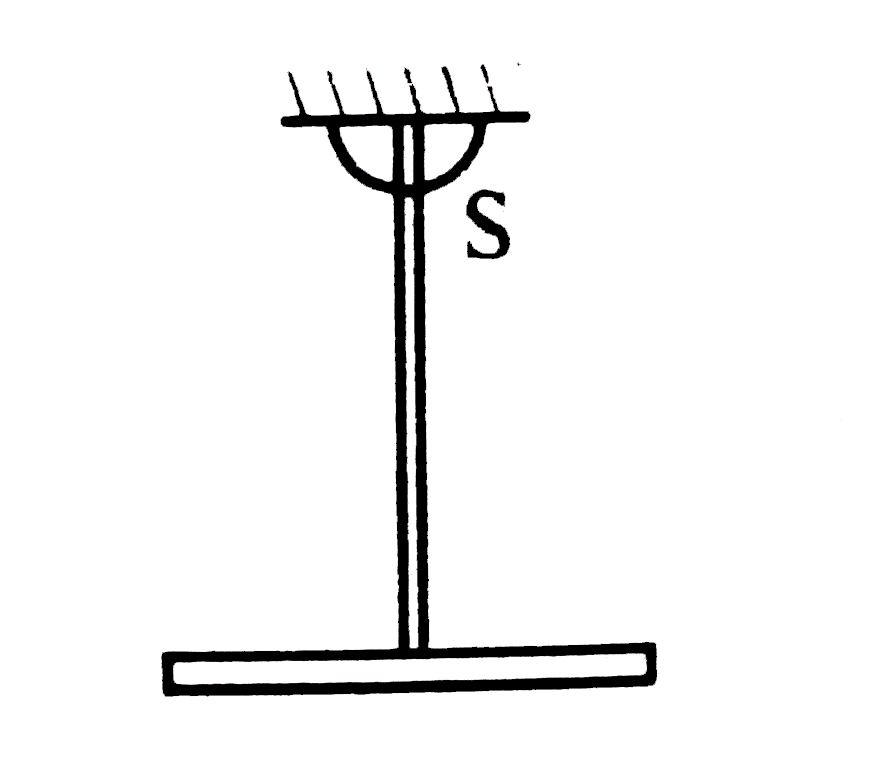
View Solution
A weightless rigid rod with a small iron bob at the end is hinged at point A to the wall so that it can rotate in all directions. The rod is kept in the horizontal position by a vertical inextensible string of length 20cm, fixed at its midpoint. The bob is displaced slightly perpenducular to the plane of the rod and string. Find period of small oscillations of the system in the form πX10s and fill the value of X.
View Solution
A weightless rigid rod with a small iron bob at the end is hinged at point A to the wall so that it can rotate in all directions. The rod is kept in the horizontal position by a vertical inextensible string of length 20cm, fixed at its midpoint. The bob is displaced slightly perpenducular to the plane of the rod and string. Find period of small oscillations of the system in the form πX10s and fill the value of X.
View SolutionA small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.

The displacement of block when equilibrium position is
View SolutionA small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.
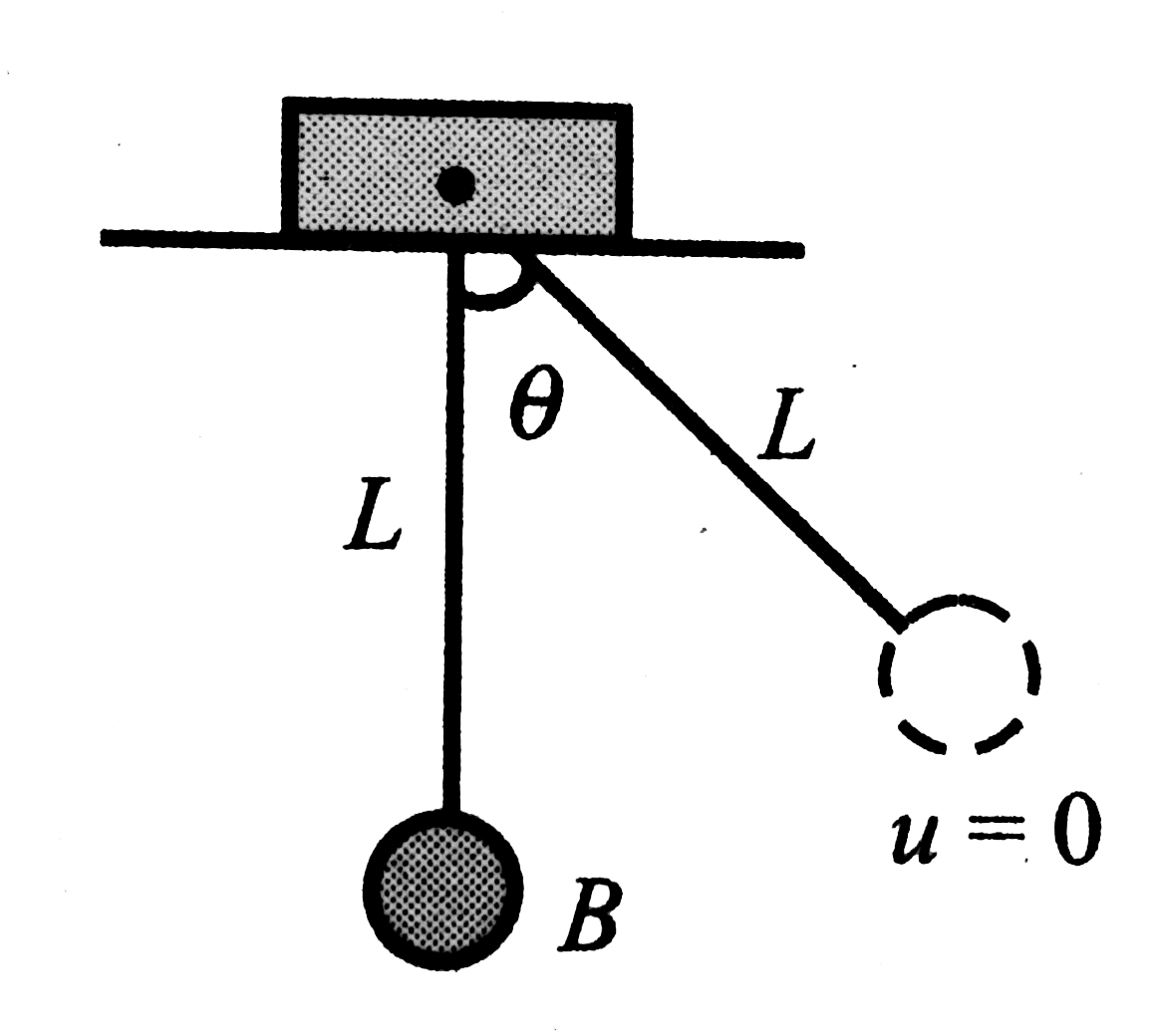 The displacement of centre of mass of A+B system till the string becomes vertical is
The displacement of centre of mass of A+B system till the string becomes vertical is
View SolutionA system of two identical rods (L-shaped) of mass m and length l are resting on a peg P as shown in the figure. If the system is displaced in its plane by a small angle θ,find the period of oscillations:

View SolutionA small ring of mass m1 is connected by a string of length l to a small heavy bob of mass m2. The ring os free to move (slide) along a fixed smooth horizontal wire. The bob is given a small displacement from its equilibrium position at right angles to string. Find period of small oscillations.
_E01_106_Q01.png)
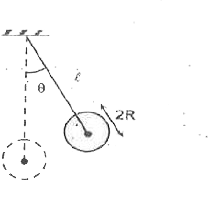
View SolutionA spherical bob of mass m and radius R is attached to a fixed point by means of a massless rigid rod whose length from the point of support up to the centre of bob is l. Find the period of small oscillation.
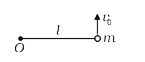
View SolutionA bob in tied to a string of length l & and kept on a horizontal rough surface as shown in the figure when point O of the string is fixed. The bob is given a tangential velocity V0 keeping the string taut as shown in figure. Find the tension in the string as a function of time. The coefficient of kinetic friction is μ.
View Solution
