A system of two identical rods (L-shaped) of mass m and length l are resting on a peg P as shown in the figure. If the system is displaced in its plane by a small angle θ,find the period of oscillations:

2π√√2l3g
2π√2√2l3g
2π√2l3g
2π√l3g
The correct Answer is:B
Center of mass 2m of a system is at a distance peg P is l2√2
_E01_027_S01.png)
τ=r×F=−mgsinθl2√2
⇒Iα=−mgsinθ=l2√2(sinθ=0 from small θ)
⇒2ml23α=−mgθl2√2⇒α=−3gθ2s√2l=−ω2θ
⇒ω=√3g2√2l⇒T=2πω=2π√2√2l3g
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-02
19 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise- 3 Match The Column
1 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - SOME WORKED OUT EXAMPLES
29 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
24 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
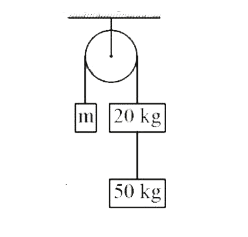
Find the mass m in the figure for the system to be at rest
View SolutionFour identical uniform thin rods, each of mass m and length l are joined to a common point O as shown in the figure. Moment of inertia of the system about an axis passing through O and lying in the plane of rods is
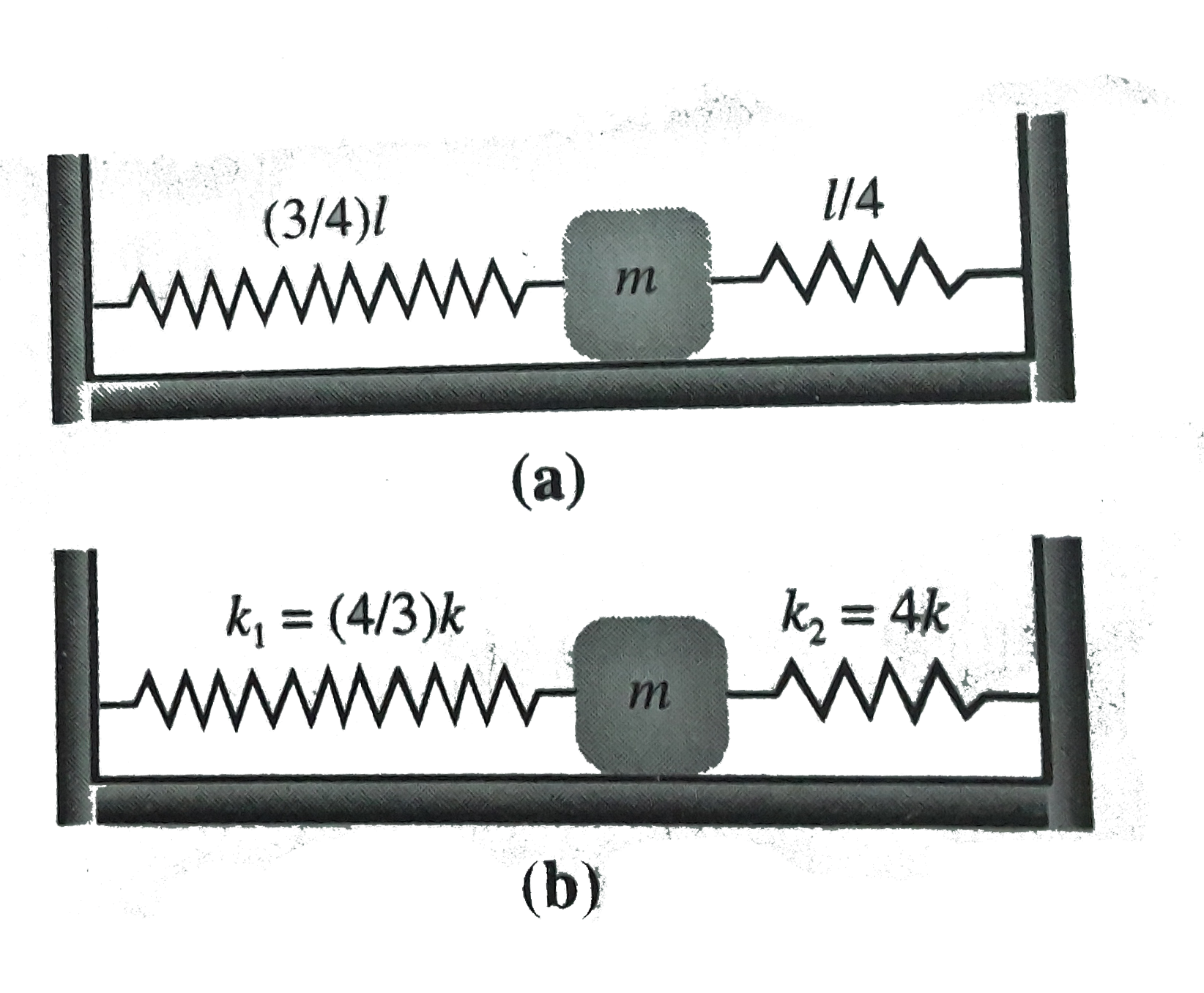
View SolutionA spring of stiffness constant k and natural length l is cut into two parts of length 3l/4andl/4, respectively, and an arrangement is made as shown in figure . If the mass is slightly displaced , find the time period of oscillation.
View SolutionTwo uniform rods each of mass M and length L are joined as shown in the figure. The moment of inertia of the system about line AB is kML2.Find the value of k.
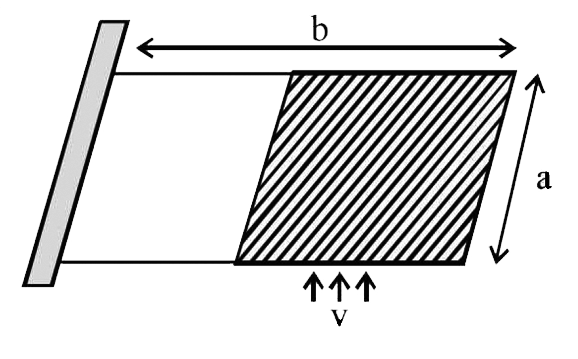
View SolutionTwo identical ladders, each of mass M and length L are resting on the rough horizontal surface as shown in the figure. A block of mass m hangs from P. if the system is in equilibrium, find the magnitude and the direction of frictional force at A and B.
View Solution
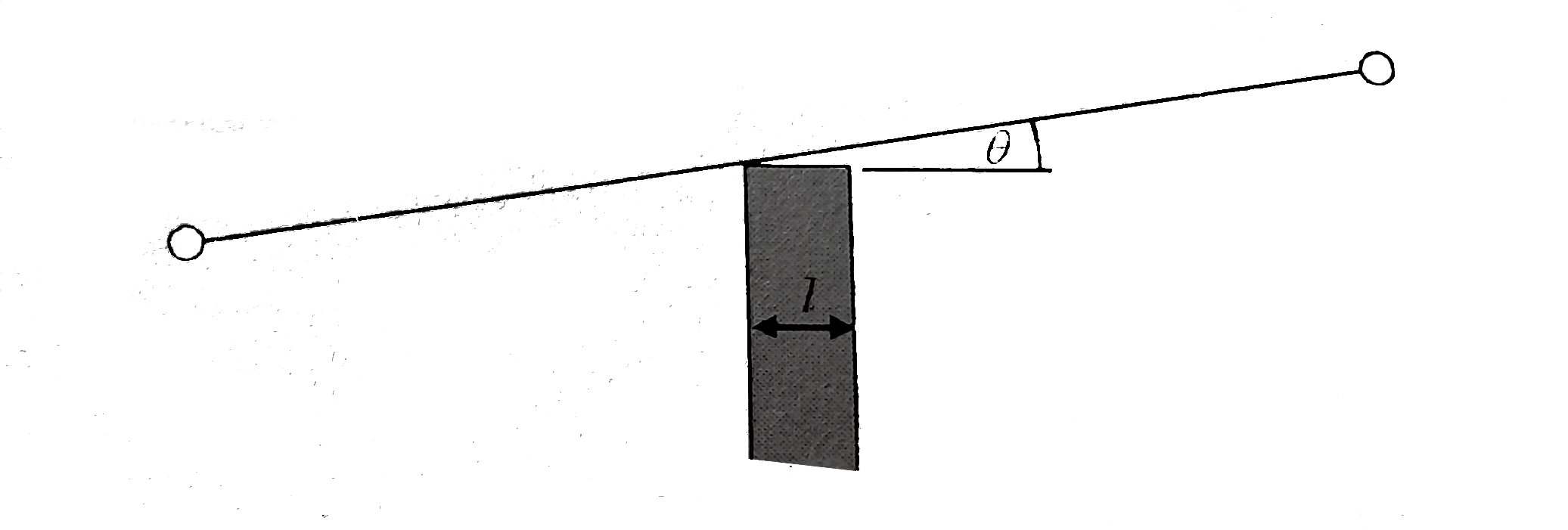
A wire is bent an an angle θ. A rod of mass m can slide along the bended wire without friction as shown in Fig. A soap film is maintained in the frame kept in a vertical position and the rod is in equilibrium as shown in the figure. If rod is displaced slightly in vertical direction, then the time period of small oscillation of the rod is
View Solution
A wire is bent an an angle θ. A rod of mass m can slide along the bended wire without friction as shown in Fig. A soap film is maintained in the frame kept in a vertical position and the rod is in equilibrium as shown in the figure. If rod is displaced slightly in vertical direction, then the time period of small oscillation of the rod is
View SolutionTwo identical rods each of mass M and length L are kept according to figure. Find the moment of inertia of rods about an axis passing through O and perpendicular to the plane of rods.

View SolutionTwo identical small balls each of mass m are rigidly affixed at the ends of light rigid rod of length 1.5m and the assmebly is placed symmetrically on an elevated protrusion of width l as shown in the figure.
The rod-ball assmebly is titled by a small angle theta in the vertical plane as shown in the figure and released. Estimate time-period (in seconds) of the oscillation of the rod-ball assembly assuming collisions of the rod with corners of the protrusion to be perfectly elastic and the rod does not slide on the corners. Assume θ=gl (numerically in radians), where g is the acceleration of free fall.
View SolutionA rod of length 2l is bent as shown in figure. Coordinates of centre of mass are
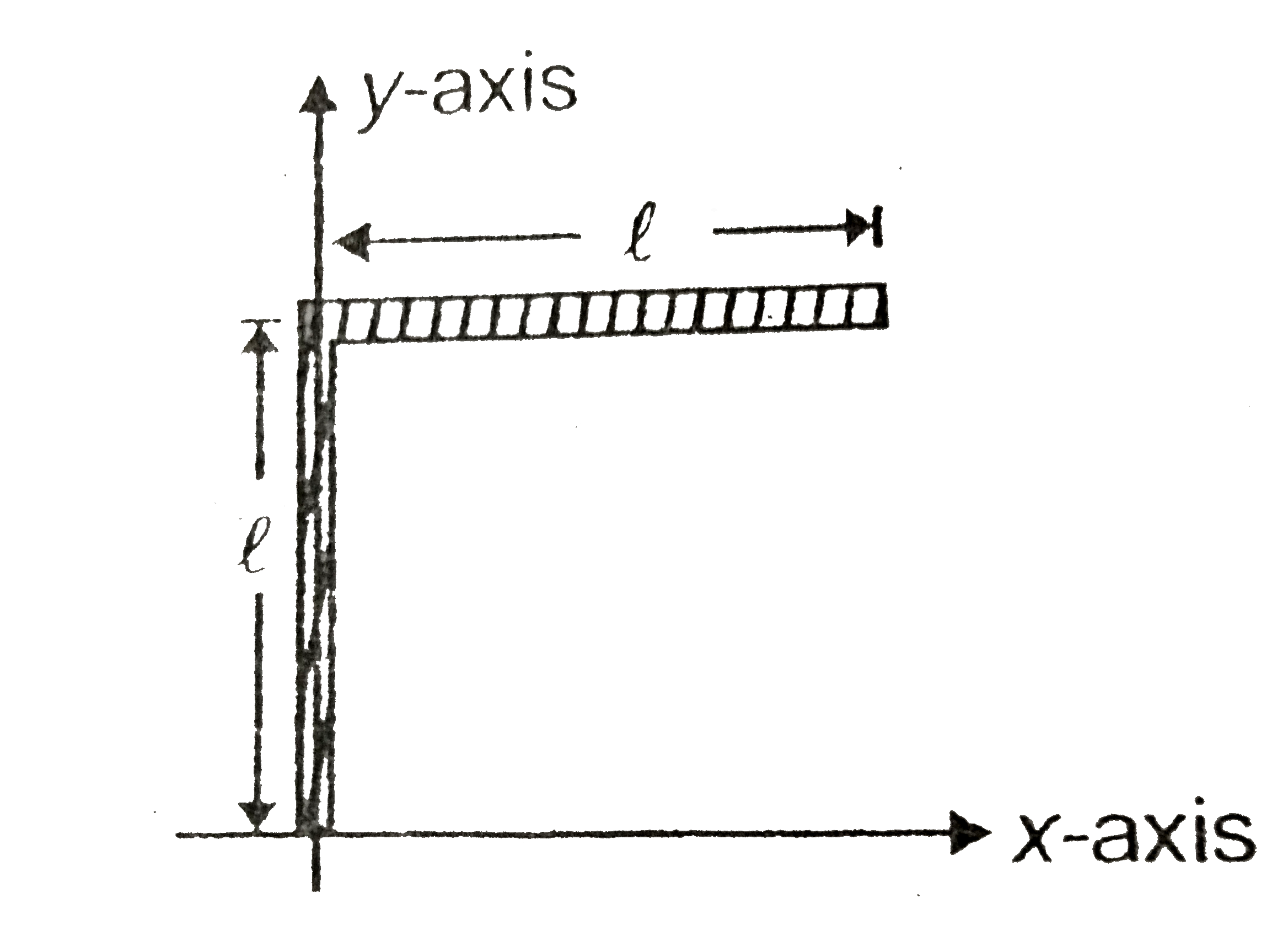
View Solution
