A disc of mass 3 m and a disc of mass m are connected by a massless spring of stiffness k. The heavier disc is placed on the ground with the spring vertical and lighter disc on top from its equilibrium position the upper disc is pushed down by a distance δ and released. Then.
if δ>3mg/k, the lower disc will bounce up
if δ=2mg/k, maximum normal reaction from ground on lower disc =6mg
if δ=2mg/k, maximum normal reaction from ground on lower disc =4mg
if δ>4mg/k, the lower disc will bounce up
The correct Answer is:B, D
From energy conservation
_E01_067_Q01.png)
12kδ12=mg(δ1+x1)+12kx12
⇒δ12−2mgkδ1=15m2g2k2=0
⇒δ1=5mgk=δ=4mgk
⇒ If δ≥4mgk the lower disk will bounce up.
Now if δ=2mgk then maximum normal reaction
from ground on lower disk
N=3mg+k(x0+δ)=6mg
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise- 3 Match The Column
Explore 1 Video
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Match The Column
Explore 9 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise-01
Explore 117 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 24 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
Similar Questions
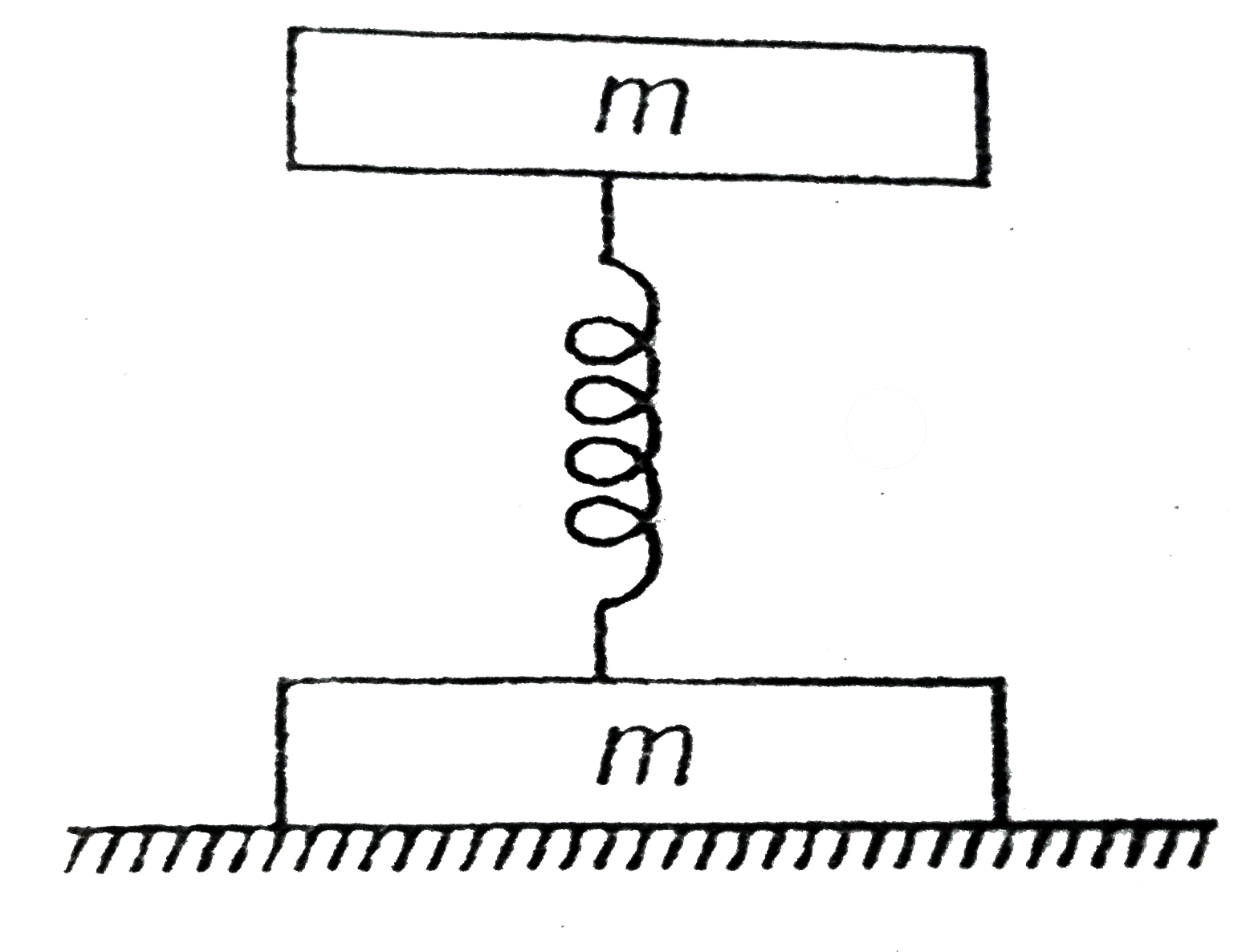
Figure shows two discs of same mass m. They are rigidy attached to a spring of stiffness k. The system is in equlibrium. From this equilibrium position, the upper disc is pressed down slowly by a distance x and released. Find the minimum value of x, if the lower disc is just lifted off the ground.
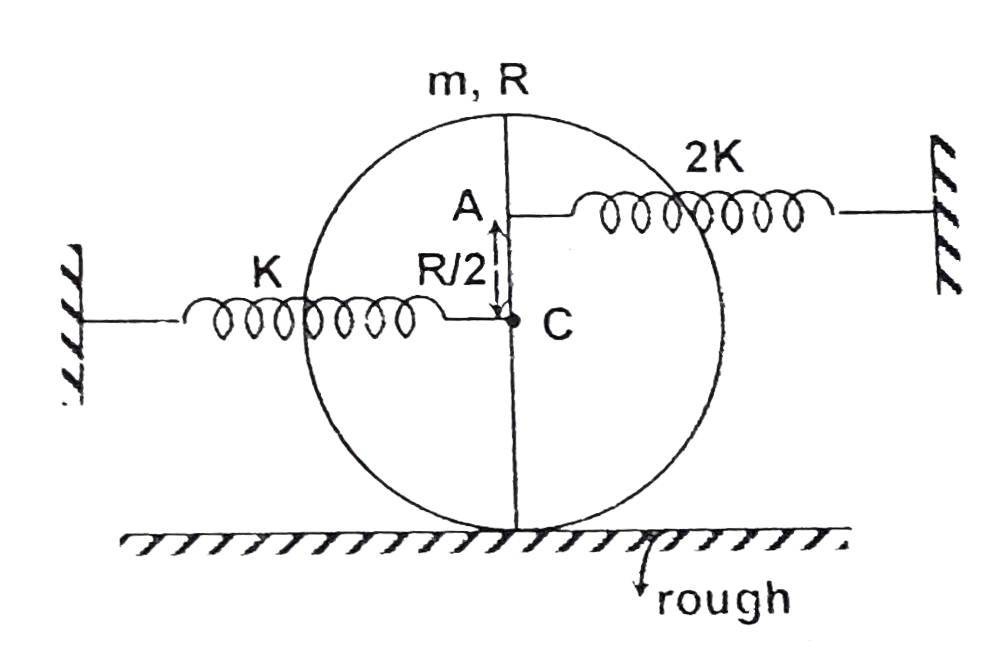
View SolutionA uniform circular disc of mass 'm' and radius 'R' is placed on a rough horizontal surface and connected to the two ideal non-deformed spring of stiffness k and 2k at the centre 'C' and point 'A' as shown . The centre of the disc is slighty displaced horizontally from equilibrium positon and then released, then the time period of small oscillation of the disc is (there is no slipping between the disc and the surface).
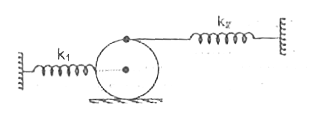
View SolutionA disk of mass m is connected to two springs of stiffness k1andk2 as shown in the figure. Find the angular frequency of the system for small oscillation. Disc can roll on the surface without slipping
View SolutionA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Force of friction between the disc and the plank is
View SolutionOne end of spring of spring constant k is attached to the centre of a disc of mass m and radius R and the other end of the spring connected to a rigid wall. A string is wrapped on the disc and the end A of the string (as shown in the figure) is pulled through a distance a and then released.
The disc is placed on a horizontal rough surface and there is no slipping at any contact point. What is the amplitude of the oscillation of the centre of the disc?

View SolutionA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Acceleration of the plank is
View SolutionA disc of mass 5 kg and radius 50 cm rolls on the ground at the rate of 10ms−1. Calculate the K.E. of the disc.
View Solution
A uniform disc of mass m and radius R is pivoted smoothly at its centre of mass. A light spring of stiffness k is attached with the dics tangentially as shown in the Fig. Find the angular frequency in rads of torsional oscillation of the disc. (Take m=5kg and K=10Nm.)
View Solution
A uniform disc of mass m and radius R is pivoted smoothly at its centre of mass. A light spring of stiffness k is attached with the dics tangentially as shown in the Fig. Find the angular frequency in rads of torsional oscillation of the disc. (Take m=5kg and K=10Nm.)
View SolutionA uniform disc of mass M and radius R is mounted on a fixed horizontal axis. A block of mass m hangs from a massless string that is wrapped around the rim of the disc. The magnitude of the acceleration of the falling block (m) is
View Solution

