A cylindrical block of the density ρ is partically immersed in a liwuid of density 3ρ. The plane surface of the block remains parallel to the surface of the liquid. The height of the block is 60m. The block perform SHM when displaced form its mean position [Use g=9.8m/s2]
the maximum amplitude is 20cm.
the maximum amplitude is 40cm
the time period will be 2π/7 seconds
none
The correct Answer is:A, C
To solve the problem step by step, we will analyze the forces acting on the cylindrical block and derive the expression for the time period of the simple harmonic motion (SHM) it undergoes when displaced from its equilibrium position.
Step 1: Understanding the Forces
When the block is partially immersed in the liquid, the buoyant force Fb acting on the block is equal to the weight of the liquid displaced by the submerged part of the block.
The buoyant force can be expressed as:
Fb=density of liquid×volume submerged×g
Given that the density of the liquid is 3ρ and the volume submerged when displaced by a distance y is A⋅y (where A is the cross-sectional area of the block), we have:
Fb=3ρ⋅A⋅y⋅g
Step 2: Weight of the Block
The weight W of the block is given by:
W=density of block×volume of block×g=ρ⋅A⋅60⋅g
Step 3: Setting Up the Equation
At equilibrium, the buoyant force equals the weight of the block:
3ρ⋅A⋅60⋅g=ρ⋅A⋅60⋅g
However, when the block is displaced by y, the new buoyant force becomes:
Fb=3ρ⋅A⋅(60−y)⋅g
The weight of the block remains the same. The net force F acting on the block when displaced is:
F=Fb−W=3ρ⋅A⋅(60−y)⋅g−ρ⋅A⋅60⋅g
Simplifying this, we get:
F=3ρ⋅A⋅(60−y)⋅g−3ρ⋅A⋅20⋅g
F=3ρ⋅A⋅g⋅(60−y−20)=3ρ⋅A⋅g⋅(40−y)
Step 4: Restoring Force and SHM
The restoring force F can be expressed as:
F=−k⋅y
where k is the effective spring constant. From the previous equation, we can identify:
k=3ρ⋅A⋅g
Thus, the equation for SHM becomes:
F=−3ρ⋅A⋅g⋅y
Step 5: Finding the Time Period
The time period T of SHM is given by:
T=2π√mk
where m is the mass of the block:
m=ρ⋅A⋅60
Substituting for k:
T=2π√ρ⋅A⋅603ρ⋅A⋅g=2π√603g=2π√20g
Substituting g=9.8m/s2:
T=2π√209.8=2π√10049=2π⋅107=20π7
Final Answer
Thus, the time period T of the SHM is:
T=20π7s
When the block is partially immersed in the liquid, the buoyant force Fb acting on the block is equal to the weight of the liquid displaced by the submerged part of the block.
Fb=density of liquid×volume submerged×g
Given that the density of the liquid is 3ρ and the volume submerged when displaced by a distance y is A⋅y (where A is the cross-sectional area of the block), we have:
Fb=3ρ⋅A⋅y⋅g
The weight W of the block is given by:
W=density of block×volume of block×g=ρ⋅A⋅60⋅g
At equilibrium, the buoyant force equals the weight of the block:
3ρ⋅A⋅60⋅g=ρ⋅A⋅60⋅g
However, when the block is displaced by y, the new buoyant force becomes:
Fb=3ρ⋅A⋅(60−y)⋅g
The weight of the block remains the same. The net force F acting on the block when displaced is:
F=Fb−W=3ρ⋅A⋅(60−y)⋅g−ρ⋅A⋅60⋅g
Simplifying this, we get:
F=3ρ⋅A⋅(60−y)⋅g−3ρ⋅A⋅20⋅g
F=3ρ⋅A⋅g⋅(60−y−20)=3ρ⋅A⋅g⋅(40−y)
The restoring force F can be expressed as:
F=−k⋅y
where k is the effective spring constant. From the previous equation, we can identify:
k=3ρ⋅A⋅g
Thus, the equation for SHM becomes:
F=−3ρ⋅A⋅g⋅y
The time period T of SHM is given by:
T=2π√mk
where m is the mass of the block:
m=ρ⋅A⋅60
Substituting for k:
T=2π√ρ⋅A⋅603ρ⋅A⋅g=2π√603g=2π√20g
Substituting g=9.8m/s2:
T=2π√209.8=2π√10049=2π⋅107=20π7
Thus, the time period T of the SHM is:
T=20π7s
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise- 3 Match The Column
1 Video
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Match The Column
9 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-01
117 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
24 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
A ball of mass m and density ρ is immersed in a liquid of density 3ρ at a depth h and released. To what height will the ball jump up above the surface of liqud ? (neglect the reistance of water and air).
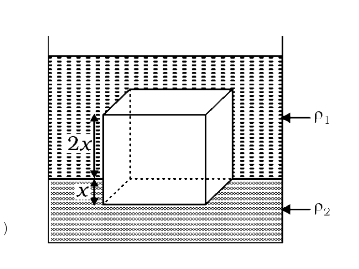
View SolutionA cubical block of density ρ floats completely immersed in two non-mixing liquids of densities ρ1andρ2 as shown in figure. The relation between ρ,ρ1andρ2 is :
View SolutionA block of density ρ floats in a liquid with its one third volume immersed. The density of the liquid is
View SolutionA block of volume V and density ρ is floating in a liquid of density 2ρ filled in a vessel. Now the vesset starts falling freely with acceleration g. Then the volume of block inside the liquid in the falling condition is
View Solution
Cylindrical block of area of cross-section A and of material of density ρ is placed in a liquid of density one third of density of block. The block compress in the spring is one-third of the length of the block. if acceleration due to gravity is g, the spring constant of the spring is
View Solution_E01_231_Q01.png)
A cylindrical rod of length l=2m & density ρ2 floats vertically in a liquid of density ρ as shown in figure. Show that it performs SHM when pulled slightly up & released find its time period. Neglect change in liquid level.
View SolutionA cubical block of wood of edge a and density ρ floats in water of density 2ρ. The lower surface of the cube just touches the free end of a mass less spring of force constant K fixed at the bottom of the vessel. The weight W put over the block so that it is completely immersed in water without wetting the weight is
View SolutionA uniform cube of mass M is floating on the surface of a liquid with three fourth of its volume immersed in the liquid (density=ρ). The length of the side of the cube is equal to

View SolutionPassage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)
Under equilibrium conditions
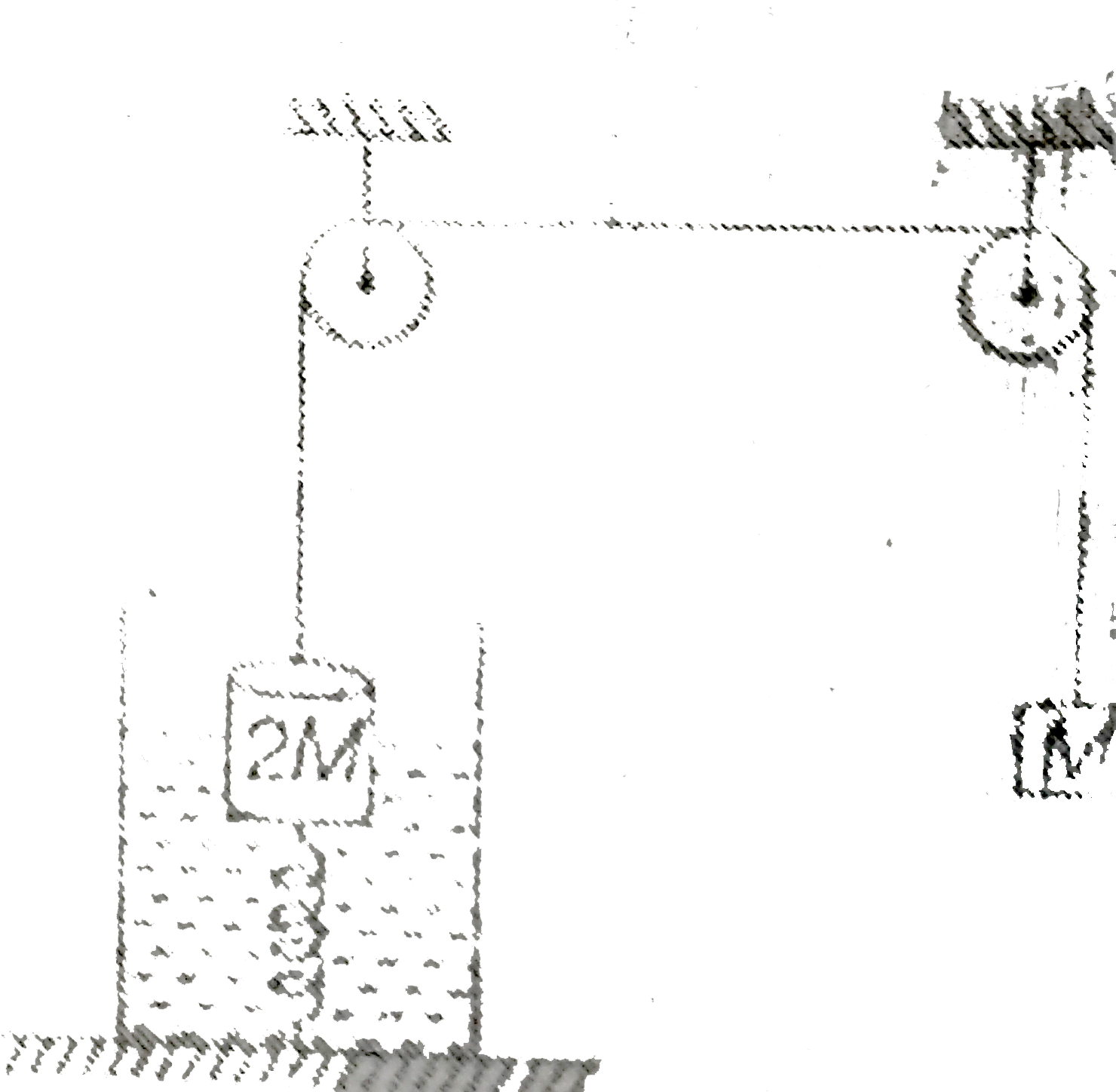
View SolutionPassage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)

By what maximum distance cylinder will be pushed downward into the liquid from equilibrium position so that when it is set free then tension in the string will not vanish [Assume at equilibrium position system was at rest]
View Solution
